Download as PDF, PPTX
Uploaded by台灣量化交易協會
Combination portfolio
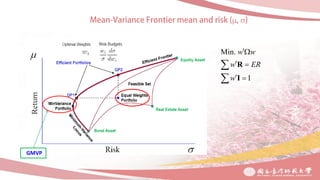
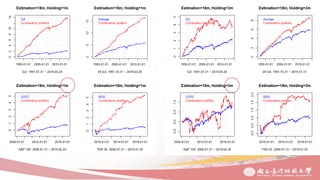
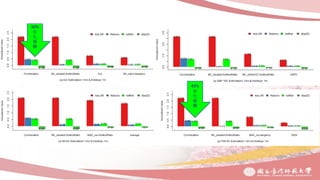
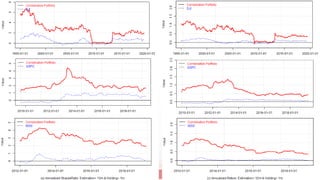
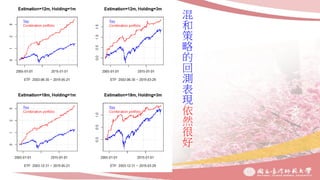
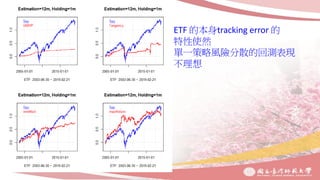
1. The document discusses combination portfolio optimization and its performance compared to other strategies through backtesting. 2. The optimal combination portfolio is found to be rebalancing every 1 month with an 18-month training period, which improves its robustness. 3. Combination portfolio is shown to outperform single strategies substantially, especially when diversifying across different asset classes and industries. However, its performance deteriorates when the holding period is extended beyond 1 month.
![Awareness of digital currency[1] (1).pptx](https://cdn.slidesharecdn.com/ss_thumbnails/awarenessofdigitalcurrency11-260125155504-b1badee4-thumbnail.jpg?width=640&height=640&fit=bounds)
Combination portfolio
- 1. Combination Portfolio - CocktailTherapy to Robust Portfolio By 何宗武 教授 臺師大管理學院 全球經營與策略研究所 tsungwu@ntnu.edu.tw http://web.ntnu.edu.tw/~tsungwu/ https://badala2164.blogspot.com/
- 2. Computation: As ofFinancial Big Data, econometrically, it is a large-scale computation with a data-based optimization with respect to various solution strategies. QP1. Min. Risk s.t. Returns QP2. Max. Returns s.t. Risk STG3. Tangency P. Max. Sharpe ratio s.t. constraints STG4. GMVP. Global minimal variance portfolios s.t. constraints
- 3. Predictive epistemology ofback-testing(training and cross-validation): If T1+T2 =13 months, be it homogeneous, without breaks & outliers Then the optimal estimates in T1+T2 are, approximately, the optimal estimates for T1 and T2 → Therefore, it calls for the robust measure of optimal estimates in T1 T2=1 backtesting ER T1=12 Min. 1 w w w ER w R I
- 4. GMVP Min. 1 w w wER w R I
- 7. ï 8 Multivariate Covariance/Correlation 25 FrontierSolution Strategies QP1 QP2 GMVP Tangency 21 Augmented Tangency Strategies Sample covariance GS Weighted LW Bayesian Shrinkage LW CC Shrinkage Multivariate student t Shrinkage SLPM Spearman
- 8. Combination Portfolio andits Solution • Cocktail Algorithm Step 1. Using 12(18)-month data as T1, we compute 250 portfolio combinations. Step 2. Computes a mean score of several performance indices, including Annualized excess returns adjusted by risk like standard deviation, VaR and CVaR, as well as skewness and kurtosis. Step 3. Pick the best one and hold 1(3) month(s) as T2. Step 4. Compute transaction fee. Step 5. Iterate • Back-testing Design 1. Estimation period T1: 12 months and 18 months 2. Holding period T2: 1 month and 3 months • Datasets: DJ30, ETF, Industry49, SP100, TWII 50
- 10. 1. Combination Portfoliooutperforms others substantially, and conditionally. 2. Its performance is restricted to 1-month rebalance frequency, it performs poorly if the holding period lengthens to 3 months. 3. Its performance is substantially enhanced when the training period slightly extends to 18 months, which improves its robustness. 4. The optimal and robust combination for optimization is (18m, 1m).
- 11. EMPIRICAL RESULTS 1 OverallComparison
- 30. EMPIRICAL RESULTS 2 SpecificResults
- 31.
- 32.
- 33.
- 34. Empirical Results 3 PerformanceRobustness Check for by rolling In stead of reporting merely a single 3-year result, to check the robustness of performance, we have to evaluate its performance at any point of time. To this end, we estimate both annualized Sharpe ratio and returns by moving windows, namely, for example: 2001/1-2013/12 2001/2-2014/1 2001/3-2014/2 …
- 36. ETF’s Challenge -- PortfolioDiversification does work --
- 37. ETF 的本身tracking error的 特性使然 單一策略風險分散的回測表現 不理想
- 38.
- 40.
- 42. 1. Combination Portfoliooutperforms others substantially, and conditionally. Most importantly, it improves robustness. 2. Its performance is restricted to 1-month rebalance frequency, it performs poorly if the holding period increases. 3. Its performance is substantially enhanced when the training period slightly extends to 18 months, which improves its robustness. 4. The optimal and robust combination for optimization is (18m, 1m).
- 43. T2 backtesting ER T1 How fardo we go? Comparing back-testing ER with implied ER Implied ER T1
- 44. How far dowe go?
- 50. Road Ahead • BusinessModel for Robo-Advisor • Optimization – The selection requires a robust standard to improve the robustness. – Tentatively, principal component score and nonparametric methods can be developed and employed. • Machine Learning can help improve the gap. • Optimal T1 and T2 are time-varying, which challenge Machine Learning.