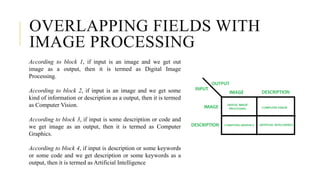
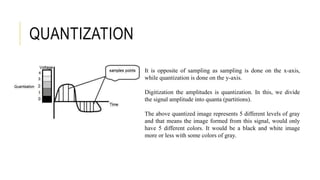
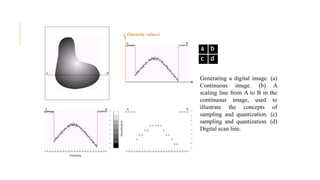
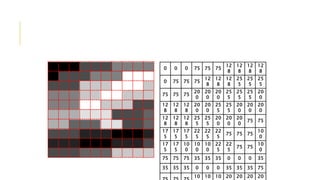
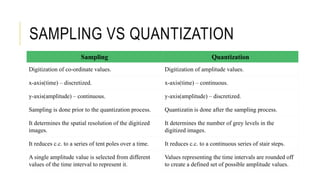
Digital image processing refers to manipulating, enhancing, and analyzing digital images using computer algorithms and techniques. It involves applying mathematical operations to digital images, which are treated as two-dimensional arrays of pixels where each pixel represents a point of color and brightness. The basic steps in digital image processing are image acquisition, enhancement, restoration, segmentation, representation/description, analysis, synthesis/compression. Digital image processing is widely used in applications like medical imaging, computer vision, and multimedia.