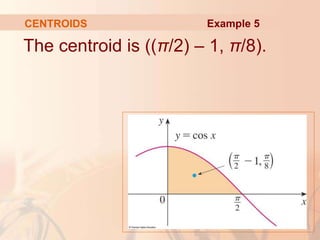
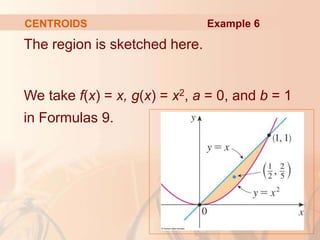
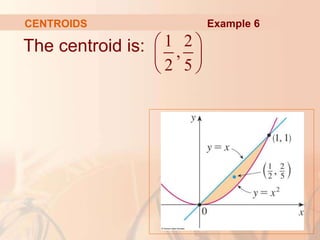
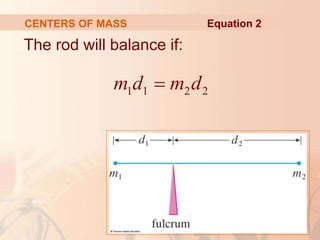
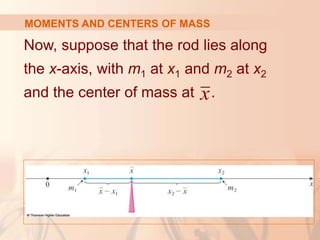
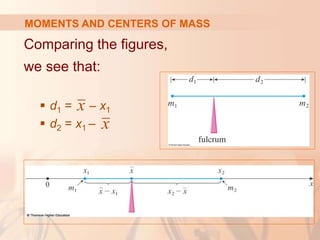
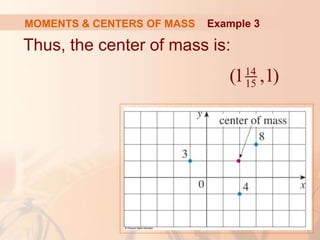
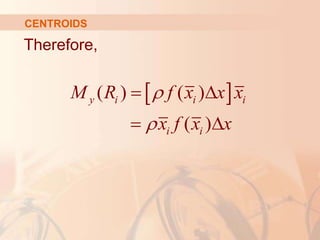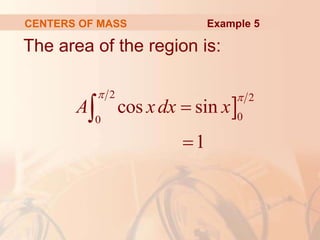This document discusses applications of integral calculus to physics and engineering problems involving force, pressure, and centers of mass. It provides examples of using integrals to calculate the hydrostatic force on structures like dams and cylinders submerged in water. It also explains how to find the center of mass of an object or system of point masses by taking moments about axes and dividing by total mass. Formulas are given for calculating hydrostatic pressure, moments, and centers of mass in one and two dimensions.

1. FURTHER APPLICATIONS
OF INTEGRATION
8

2. 8.3
Applications to
Physics and Engineering
In this section, we will learn about:
The applications of integral calculus to
force due to water pressure and centers of mass.
FURTHER APPLICATIONS OF INTEGRATION

3. As with our previous applications to geometry
(areas, volumes, and lengths) and to work,
our strategy is:
 Break up the physical quantity into small parts.
 Approximate each small part.
 Add the results.
 Take the limit.
 Then, evaluate the resulting integral.
APPLICATIONS TO PHYSICS AND ENGINEERING

4. Deep-sea divers realize that water
pressure increases as they dive deeper.
 This is because the weight of the water
above them increases.
HYDROSTATIC FORCE AND PRESSURE

5. Suppose that a thin plate with area A m2 is
submerged in a fluid of density ρ kg/m3 at a
depth d meters below the surface of the fluid.
HYDROSTATIC FORCE AND PRESSURE

6. The fluid directly above the plate has volume
V = Ad
So, its mass is:
m = ρV = ρAd
HYDROSTATIC FORCE AND PRESSURE

7. Thus, the force exerted by the fluid on
the plate is
F = mg = ρgAd
where g is the acceleration due to gravity.
HYDROSTATIC FORCE

8. The pressure P on the plate is defined
to be the force per unit area:
HYDROSTATIC PRESSURE
F
P gd
A

 

9. The SI unit for measuring pressure is newtons
per square meter—which is called a pascal
(abbreviation: 1 N/m2 = 1 Pa).
 As this is a small unit, the kilopascal (kPa)
is often used.
HYDROSTATIC PRESSURE

10. For instance, since the density of water is
ρ = 1000 kg/m3, the pressure at the bottom
of a swimming pool 2 m deep is:
HYDROSTATIC PRESSURE
3 2
1000kg/m 9.8m/s 2m
19,600Pa
19.6kPa
P gd


  



11. An important principle of fluid pressure is
the experimentally verified fact that, at any
point in a liquid, the pressure is the same in
all directions.
 This is why a diver feels the same pressure
on nose and both ears.
HYDROSTATIC PRESSURE

12. Thus, the pressure in any direction at
a depth d in a fluid with mass density ρ
is given by:
HYDROSTATIC PRESSURE
P gd d
 
 
Equation 1

13. This helps us determine the hydrostatic
force against a vertical plate or wall or dam
in a fluid.
 This is not a straightforward problem.
 The pressure is not constant, but increases
as the depth increases.
HYDROSTATIC FORCE AND PRESSURE

14. A dam has the shape of the trapezoid
shown below.
 The height is 20 m.
 The width is 50 m at the top and 30 m at the bottom.
HYDROSTATIC F AND P Example 1

15. Find the force on the dam due to
hydrostatic pressure if the water level
is 4 m from the top of the dam.
HYDROSTATIC F AND P Example 1

16. We choose a vertical x-axis with origin
at the surface of the water.
HYDROSTATIC F AND P Example 1

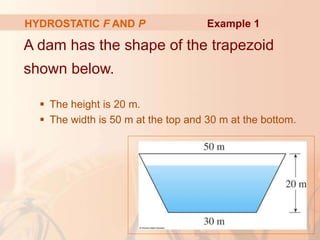
17. The depth of the water is 16 m.
 So, we divide the interval [0, 16] into subintervals
of equal length with endpoints xi.
 We choose
xi* [xi–1, xi].
HYDROSTATIC F AND P Example 1


18. The i th horizontal strip of the dam is
approximated by a rectangle with height Δx
and width wi
HYDROSTATIC F AND P Example 1

19. From similar triangles,
HYDROSTATIC F AND P
* *
*
16
10
or 8
16 20 2 2
i i
i
x x
a
a
x

   

Example 1

20. Hence,
*
1
2
*
2(15 )
2(15 8 )
46
i
i
i
w a
x
x
 
  
 
HYDROSTATIC F AND P Example 1

21. If Ai is the area of the strip, then
If Δx is small, then the pressure Pi on the i th
strip is almost constant, and we can use
Equation 1 to write:
HYDROSTATIC F AND P
*
(46 )
i i i
A w x x x
    
*
1000
i i
P gx

Example 1

22. The hydrostatic force Fi acting on the i th
strip is the product of the pressure and
the area:
HYDROSTATIC F AND P
* *
1000 (46 )
i i i
i i
F PA
gx x x

  
Example 1

23. Adding these forces and taking the limit as
n → ∞, the total hydrostatic force on the dam
is:
HYDROSTATIC F AND P
* *
1
16
0
16
2
0
16
3
2 7
0
lim 1000 (46 )
1000 (46 )
1000(9.8) (46 )
9800 23 4.43 10 N
3
n
i i
n
i
F gx x x
gx x dx
x x dx
x
x


  
 
 
 
   
 
 



Example 1

24. Find the hydrostatic force on one end of
a cylindrical drum with radius 3 ft, if the drum
is submerged in water
10 ft deep.
HYDROSTATIC F AND P Example 2

25. In this example, it is convenient to choose
the axes as shown—so that the origin is
placed at the center
of the drum.
 Then, the circle has
a simple equation:
x2 + y2 = 9
HYDROSTATIC F AND P Example 2

26. As in Example 1, we divide the circular
region into horizontal strips of equal width.
HYDROSTATIC F AND P Example 2

27. From the equation of the circle, we see that
the length of the i th strip is:
So, its area is:
HYDROSTATIC F AND P
* 2
2 9 ( )
i
y

* 2
2 9 ( )
i i
A y y
  
Example 2

28. The pressure on this strip is approximately
So, the force on the strip is approximately
HYDROSTATIC F AND P
* * 2
62.5(7 )2 9 ( )
i i i i
d A y y y
    
*
62.5(7 )
i i
d y
  
Example 2

29. We get the total force by adding the forces
on all the strips and taking the limit:
HYDROSTATIC F AND P
* * 2
1
3
2
3
3 3
2 2
3 3
lim 62.5(7 )2 9 ( )
125 (7 ) 9
125 7 9 125 9
n
i i
n
i
F y y y
y y dy
y dy y y dy



 
   
  
    


 
Example 2

30. The second integral is 0 because
the integrand is an odd function.
 See Theorem 7 in Section 5.5
HYDROSTATIC F AND P Example 2

31. The first integral can be evaluated using
the trigonometric substitution y = 3 sin θ.
However, it’s simpler to observe that it is
the area of a semicircular disk with radius 3.
HYDROSTATIC F AND P Example 2

32. Thus,
HYDROSTATIC F AND P
3
2
3
2
1
2
875 9
875 (3)
7875
2
12,370lb
F y dy



 
 



Example 2

33. Our main objective here is to find the point P
on which a thin plate of any given shape
balances horizontally as shown.
MOMENTS AND CENTERS OF MASS

34. This point is called the center of mass
(or center of gravity) of the plate.
CENTERS OF MASS

35. We first consider the simpler
situation illustrated here.
CENTERS OF MASS

36. Two masses m1 and m2 are attached to
a rod of negligible mass on opposite sides
of a fulcrum and at distances d1 and d2 from
the fulcrum.
CENTERS OF MASS

37. The rod will balance if:
CENTERS OF MASS
1 1 2 2
m d m d

Equation 2

38. This is an experimental fact discovered by
Archimedes and called the Law of the Lever.
 Think of a lighter person balancing a heavier one
on a seesaw by sitting farther away from the center.
LAW OF THE LEVER

39. Now, suppose that the rod lies along
the x-axis, with m1 at x1 and m2 at x2
and the center of mass at .
MOMENTS AND CENTERS OF MASS
x

40. Comparing the figures,
we see that:
 d1 = – x1
 d2 = x1 –
x
MOMENTS AND CENTERS OF MASS
x

41. CENTERS OF MASS
So, Equation 2 gives:
1 1 2 2
( ) ( )
m x x m x x
  
1 2 1 1 2 2
m x m x m x m x
  
1 1 2 2
1 2
m x m x
x
m m



Equation 3

42. The numbers m1x1 and m2x2 are called
the moments of the masses m1 and m2
(with respect to the origin).
MOMENTS OF MASS

43. Equation 3 says that the center of mass
is obtained by:
1. Adding the moments of the masses
2. Dividing by the total mass m = m1 + m2
MOMENTS OF MASS
x
1 1 2 2
1 2
m x m x
x
m m




44. In general, suppose we have a system of n
particles with masses m1, m2, . . . , mn located
at the points x1, x2, . . . , xn on the x-axis.
Then, we can show where the center of mass
of the system is located—as follows.
CENTERS OF MASS Equation 4

45. The center of mass of the system is
located at
where m = Σ mi is the total mass of
the system.
CENTERS OF MASS
1 1
1
n n
i i i i
i i
n
i
i
m x m x
x
m
m
 

 
 

Equation 4

46. The sum of the individual moments
is called the moment of the system
about the origin.
MOMENT OF SYSTEM ABOUT ORIGIN
1
n
i i
i
M m x

 

47. Then, Equation 4 could be rewritten
as:
m = M
 This means that, if the total mass were considered
as being concentrated at the center of mass ,
then its moment would be the same as the moment
of the system.
MOMENT OF SYSTEM ABOUT ORIGIN
x
x

48. Now, we consider a system of n particles with
masses m1, m2, . . . , mn located at the points
(x1, y1), (x2, y2) . . . , (xn, yn) in the xy-plane.
MOMENTS AND CENTERS OF MASS

49. By analogy with the one-dimensional case,
we define the moment of the system about
the y-axis as
and the moment of the system about
the x-axis as
MOMENT ABOUT AXES
1
n
y i i
i
M m x

 
Equations 5 and 6
1
n
x i i
i
M m y

 

50. My measures the tendency of the system
to rotate about the y-axis.
Mx measures the tendency of the system
to rotate about the x-axis.
MOMENT ABOUT AXES

51. As in the one-dimensional case,
the coordinates of the center of mass
are given in terms of the moments by
the formulas
where m = ∑ mi is the total mass.
CENTERS OF MASS
( , )
x y
y x
M M
x y
m m
 
Equation 7

52. Since ,
the center of mass is the point
where a single particle of mass m would
have the same moments as the system.
MOMENTS AND CENTERS OF MASS
and
y x
mx M my M
 
( , )
x y

53. Find the moments and center of mass
of the system of objects that have masses
3, 4, and 8 at the points (–1, 1), (2, –1) and
(3, 2) respectively.
MOMENTS & CENTERS OF MASS Example 3

54. We use Equations 5 and 6 to compute
the moments:
MOMENTS & CENTERS OF MASS
3( 1) 4(2) 8(3) 29
3(1) 4( 1) 8(2) 15
y
x
M
M
    
    
Example 3

55. As m = 3 + 4 + 8 = 15, we use Equation 7
to obtain:
MOMENTS & CENTERS OF MASS Example 3
29 15
1
15 15
y x
M M
x y
m m
    

56. Thus, the center of mass is:
MOMENTS & CENTERS OF MASS
14
15
(1 ,1)
Example 3

57. Next, we consider a flat plate, called
a lamina, with uniform density ρ that
occupies a region R of the plane.
 We wish to locate the center of mass of the plate,
which is called the centroid of R .
CENTROIDS

58. In doing so, we use
the following physical
principles.
CENTROIDS

59. The symmetry principle says that, if R is
symmetric about a line l, then the centroid
of R lies on l.
 If R is reflected about l, then R remains the same
so its centroid remains fixed.
 However, the only fixed points lie on l.
 Thus, the centroid of a rectangle is its center.
CENTROIDS

60. Moments should be defined so that, if
the entire mass of a region is concentrated
at the center of mass, then its moments
remain unchanged.
CENTROIDS

61. Also, the moment of the union of two
non-overlapping regions should be
the sum of the moments of the individual
regions.
CENTROIDS

62. Suppose that the region R is of the type
shown here.
That is, R lies:
 Between the lines
x = a and x = b
 Above the x-axis
 Beneath the graph
of f, where f is a
continuous function
CENTROIDS

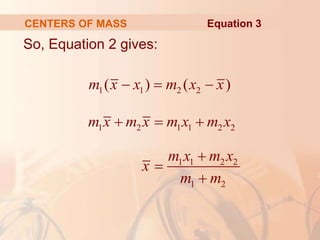
63. We divide the interval [a, b] into n subintervals
with endpoints x0, x1, . . . , xn and equal width
∆x.
 We choose the
sample point xi
* to
be the midpoint
of the i th
subinterval.
 That is,
= (xi–1 + xi)/2
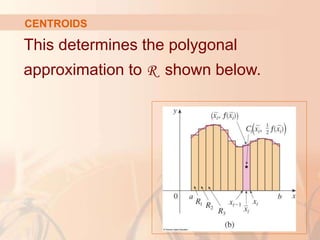
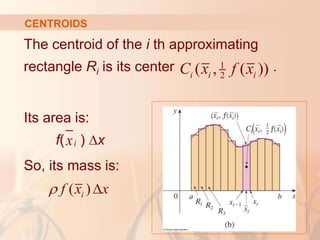
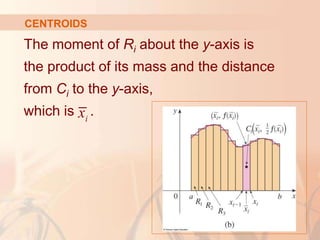
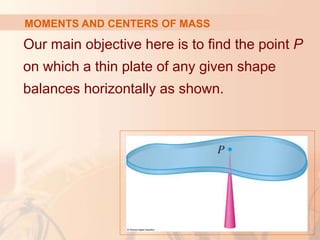
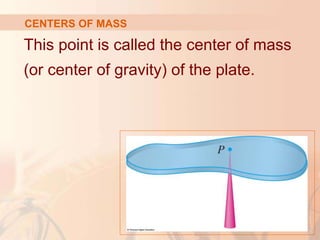
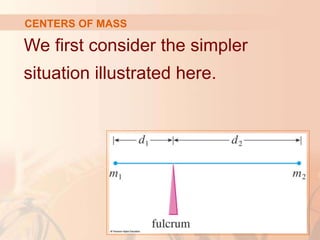
CENTROIDS
i
x
i
x

64. This determines the polygonal
approximation to R shown below.
CENTROIDS

65. The centroid of the i th approximating
rectangle Ri is its center .
Its area is:
f( ) ∆x
So, its mass is:
CENTROIDS
1
2
( , ( ))
i i i
C x f x
( )
i
f x x
 
i
x

66. The moment of Ri about the y-axis is
the product of its mass and the distance
from Ci to the y-axis,
which is .
CENTROIDS
i
x

67. Therefore,
CENTROIDS
 
( ) ( )
( )
y i i i
i i
M R f x x x
x f x x


 
 

68. Adding these moments, we
obtain the moment of the polygonal
approximation to R .
CENTROIDS

69. Then, by taking the limit as n → ∞,
we obtain the moment of R itself about
the y-axis:
CENTROIDS
1
lim ( )
( )
n
y i i
n
i
b
a
M x f x x
x f x dx




 




70. Similarly, we compute the moment of Ri
about the x-axis as the product of its mass
and the distance from Ci to the x-axis:
CENTROIDS
 
 
1
2
2
1
2
( ) ( ) ( )
( )
x i i i
i
M R f x x f x
f x x


 
  

71. Again, we add these moments and take
the limit to obtain the moment of R about
the x-axis:
CENTROIDS
 
 
2
1
2
1
2
1
2
lim ( )
( )
n
x i
n
i
b
a
M f x x
f x dx




  




72. Just as for systems of particles,
the center of mass of the plate is
defined so that
CENTROIDS
and
y x
mx M my M
 

73. However, the mass of the plate is
the product of its density and its area:
CENTROIDS
( )
b
a
m A
f x dx



 

74. Thus,
 Notice the cancellation of the ρ’s.
 The location of the center of mass is independent
of the density.
CENTROIDS
( ) ( )
( ) ( )
b b
y a a
b b
a a
xf x dx xf x dx
M
x
m f x dx f x dx


  
 
 
   
2 2
1 1
2 2
( ) ( )
( ) ( )
b b
x a a
b b
a a
f x dx f x dx
M
y
m f x dx f x dx


  
 
 

75. In summary, the center of mass of the plate (or
the centroid of R ) is located at the point
, where
CENTROIDS
( , )
x y
 
2
1
2
1
( )
1
( )
b
a
b
a
x xf x dx
A
y f x dx
A




Formula 8

76. Find the center of mass of a semicircular
plate of radius r.
 To use Equation 8, we place the semicircle as shown
so that f(x) = √(r2 – x2) and a = –r, b = r.
CENTERS OF MASS Example 4

77. Here, there is no need to use the formula
to calculate .
 By the symmetry principle, the center of mass
must lie on the y-axis, so .
CENTERS OF MASS
x
0
x 
Example 4

78. The area of the semicircle is A = ½πr2.
Thus,
CENTERS OF MASS
 
 
 
2
1
2
2
2 2
1
2
2
1
2
3
2 2 2
2 2
0
0
3
2
1
( )
1
2 2
3
2 2 4
3 3
r
r
r
r
r
r
y f x dx
A
r x dx
r
x
r x dx r x
r r
r r
r

 
 



  
 
   
 
 
 



Example 4

79. The center of mass is located at
the point (0, 4r/(3π)).
CENTERS OF MASS Example 4

80. Find the centroid of the region bounded
by the curves
y = cos x, y = 0, x = 0, x = π/2
CENTERS OF MASS Example 5

81. The area of the region is:
CENTERS OF MASS

2 2
0
0
cos sin
1
A xdx x
 



Example 5

82. CENTROIDS
 
 
 
/ 2 2
1
2
/ 2
2
1
2
/ 2
1
4
/ 2
1 1
4 2 0
1
( )
cos
1 cos2
sin 2
8
a
a
a
y f x dx
A
xdx
x dx
x x







 
 




Example 5

/2
/2
0
2
0
2
0
1
( )
cos
sin
sin
1
2
a
x xf x dx
A
x xdx
x x
xdx









 



So, Formulas 8 give:

83. The centroid is ((π/2) – 1, π/8).
CENTROIDS Example 5

84. Suppose the region R lies between
two curves y = f(x) and y = g(x), where
f(x) ≥ g(x).
CENTROIDS

85. Then, the same sort of argument that led
to Formulas 8 can be used to show that
the centroid of R is , where
CENTROIDS
( , )
x y
 
   
 
2 2
1
2
1
( ) ( )
1
( ) ( )
b
a
b
a
x x f x g x dx
A
y f x g x dx
A
 
 


Formula 9

86. Find the centroid of the region
bounded by the line x = y and
the parabola y = x2.
CENTROIDS Example 6

87. The region is sketched here.
We take f(x) = x, g(x) = x2, a = 0, and b = 1
in Formulas 9.
CENTROIDS Example 6

88. First, we note that the area of the region
is:
CENTROIDS
1
2
0
1
2 3
0
( )
2 2
1
6
A x x dx
x x
 

  



Example 6

89. Therefore,
CENTROIDS
 
1
0
1
2
1 0
6
1
2 3
0
1
3 4
0
1
( ) ( )
1
( )
6 ( )
1
6
3 4 2
 
 
 
 
  
 
 



x x f x g x dx
A
x x x dx
x x dx
x x
Example 6
   
 
1 2 2
1
2
0
1
2 4
1
2
1 0
6
1
3 5
0
1
( ) ( )
1
( )
3
3 5
2
5
y f x g x dx
A
x x dx
x x
 
 
 
 
 
 




90. The centroid is:
CENTROIDS
1 2
,
2 5
 
 
 
Example 6

91. We end this section by showing
a surprising connection between
centroids and volumes of revolution.
CENTROIDS

92. Let R be a plane region that lies entirely
on one side of a line l in the plane.
If R is rotated about l, then the volume of
the resulting solid is the product of the area A
of R and the distance d traveled by
the centroid of R .
THEOREM OF PAPPUS

93. We give the proof for the special case
in which the region lies between y = f(x)
and y = g(x) as shown and the line l
is the y-axis.
THEOREM OF PAPPUS Proof

94. By the cylindrical shells method (Section 6.3),
we have:
 is the distance traveled by the centroid
during one rotation about the y-axis.
THEOREM OF PAPPUS
 
 
2 ( ) ( )
2 ( ) ( )
2 ( ) (Formulas 9)
(2 )
b
a
b
a
V x f x g x dx
x f x g x dx
xA
x A
Ad




 
 





Proof
2
d x



95. A torus is formed by rotating a circle of
radius r about a line in the plane of the circle
that is a distance R(> r) from the center of
the circle.
Find the volume of the torus.
THEOREM OF PAPPUS Example 7

96. The circle has area A = πr2.
By the symmetry principle, its centroid is
its center.
 So, the distance traveled by the centroid during
a rotation is d = 2πR.
THEOREM OF PAPPUS Example 7

97. Therefore, by the Theorem of Pappus,
the volume of the torus is:
THEOREM OF PAPPUS
2
2 2
(2 )( )
2
V Ad
R r
r R
 




Example 7

98. Compare the method of
Example 7 with that of Exercise 63
in Section 6.2
THEOREM OF PAPPUS