This document provides a summary of a hydrology course session on maximum flows. It discusses maximum flow definitions and calculations using direct methods like Manning's equation and empirical methods such as the Rational Formula. It also covers peak flow estimation using the Curve Number method considering factors like soil type, cover, and initial moisture conditions. The session concludes with recommendations for applying these methods to estimate maximum flows for hydraulic structure design.

1. CURSO: HIDROLOGÍA
V CICLO
3° UND - SESIÓN 11: Caudales máximos
Docente: Neil BALBIN LAZO, Dr. Ing. Civil, Ing. Mecánico de Fluidos
E-mail: nbalbinl@ucvvirtual.edu.pe
Facultad de Ingeniería
Escuela Profesional de Ingeniería Civil

2. Fin de la clase
1. Caudales máximos: introducción
2. Crecientes e inundaciones
3. Método Directo
4. Métodos empíricos
5. Método del numero de curva
2

3. 1. Caudales máximos
1.1 Definición
El Caudal máximo de avenidas, crecientes o
inundaciones es necesario para diseñar canales,
cunetas, alcantarillas, drenajes y para determinar el
nivel máximo.
3

4. 2. Avenida, crecientes e inundaciones
2.1 Creciente
Fenómeno de ocurrencia de grandes avenidas, que se
salen de sus cauces normales, causando inundación.
El cálculo de estas grandes avenidas, es importante
para el diseño de obras de regulación de caudales.
4

5. 2. Avenida, crecientes e inundaciones
2.2 Pronóstico de crecientes
Es válida para calcular una creciente por extrapolación
de datos históricos, en la que se produce una situación
crítica. Si se poseen n años de datos históricos y se
requiere conocer el caudal con un periodo de retorno
de m años, debe cumplirse m > n.
5

6. 2. Avenida, crecientes e inundaciones
2.3 Periodo de retorno T
Tiempo promedio en años, en que el valor del caudal
pico de una creciente determinada es igualado o
superado por lo menos una vez. Se fija considerando:
- Criterios económicos
- Criterios usuales
- Criterio de riesgo
6

7. 2. Avenida, crecientes e inundaciones
2.3 Periodo de retorno T
2.3.1 Criterios económicos
7

8. 2. Avenida, crecientes e inundaciones
2.3 Periodo de retorno T
2.3.2 Criterios usuales
- Vida útil de la obra (30 años)
- Responsabilidad del contratista: >7 años, según Art.
40 de la LCE (aprobado por Ley N° 30225, modificado
por DL 1341 del 07.01.2017)
- Tipo de estructura: presa de gravedad o presa C° A°
- Facilidad de reparación y ampliación: colmatación
- Peligro de pérdidas de vidas humanas: presa en el río
Rímac vs presa en el río Pachacamac (mapas)
8

9. 2. Avenida, crecientes e inundaciones
Cuenca río Rímac
.
9

10. 2. Avenida, crecientes e inundaciones
Cuenca río Pachacamac
.
10

11. 3. Método Directo
3.1 Formula de Manning
Procedimiento:
- Determinar la pendiente S de la superficie libre del
agua, mediante huella de avenidas máximas
- Según las condiciones del cauce, elegir coeficiente n
o determinar por el Método de Cowan
𝑛 = (𝑛0 + 𝑛1 + 𝑛2 + 𝑛3 + 𝑛4) × 𝑚5
- Calcular Qmáx de la avenida
𝑄 =
𝐴
𝑛
𝑅 ൗ
2
3𝑆 ൗ
1
2
11

12. 3. Método Directo
3.2 Manning: Método de las sub secciones
.
12

13. 3. Método Directo
3.2 Manning: Método de las sub secciones
Procedimiento:
- Se divide en subsecciones y se tiene:
Qt = Q1 + Q2 + Q3 + … + Qn
- Cada sección tiene una rugosidad: n1, n2, n3 …
- El perímetro mojado es superficie en contacto con
agua, mas no superficie de agua entre sub secciones
El caudal total:
𝑄𝑡 = 𝑆 ൗ
1
2
𝐴1
𝑛1
𝑅1
ൗ
2
3 +
𝐴2
𝑛2
𝑅2
ൗ
2
3 +
𝐴3
𝑛3
𝑅3
ൗ
2
3 + …
13

14. 3. Método Directo
3.3 Manning: Método de rugosidad compuesta
.
14

15. 3. Método Directo
3.3 Manning: Método de rugosidad compuesta
- Despejando A de Manning:
𝐴 = 𝑃 ×
𝑛 𝑉
𝑆 ൗ
1
2
ൗ
3
2
- Como S y V son constantes y:
At = A1 + A2 + A3 + … + An
- Reemplazando y operando:
𝑛 =
𝑃1 𝑛1
ൗ
3
2 + 𝑃2 𝑛2
ൗ
3
2 + …
𝑃
ൗ
2
3
15

16. 3. Método Directo
3.4 Manning: Aplicación
Se tiene la aproximación del cauce de un rio con una marca en
el cauce total de d=3.20m, y los coeficientes de rugosidad en
las ampliaciones laterales son de n2 = 0.035 y n1=0.025 en la
parte central. Calcular Qmax si S=0.00035 (hoja de cálculo)
16

17. 3. Método Directo
3.1 Manning: Método de rugosidad compuesta:
Horton y Einstein
- Despejando A de Manning:
𝐴 = 𝑃 ×
𝑛 𝑉
𝑆 ൗ
1
2
ൗ
3
2
- Como S y V son constantes y:
At = A1 + A2 + A3 + … + An
- Reemplazando y operando:
𝑛 =
𝑃1 𝑛1
ൗ
3
2 + 𝑃2 𝑛2
ൗ
3
2 + …
𝑃
ൗ
2
3
17

18. 4. Métodos empíricos
Se muestran formulas para el cálculo de caudales de
crecientes
4.1 Formula Racional
𝑄 =
𝐶 × 𝐼 × 𝐴
3.6
Q: caudal máximo de escorrentía [m3/s]
I: Intensidad máxima pp para un periodo de duración
igual al tc y para la frecuencia deseada [mm/h]
A: Superficie de cuenca [Km2]
C: Coeficiente de escorrentía, adimensional
En una pista de concreto C=1, no se infiltra nada
En un terreno arenoso C=0.1, se infiltra 9/10 18

19. 4. Métodos empíricos
4.1 Formula Racional
El límite del área de la cuenca depende de la pendiente
Debe usarse con cautela para áreas mayores a 50 Ha y
nunca para áreas mayores de 500 Ha
El valor de C está en función de las características
fisiográficas de la cuenca
La frecuencia I se obtiene de las curvas IDF
Esta fórmula se utiliza para diseñar cunetas,
alcantarillas, badenes y otras estructuras evacuadoras
de aguas de escorrentía en pequeñas cuencas
19

20. 4. Métodos empíricos
4.1 Formula Racional
.
20

21. 4. Métodos empíricos
4.1 Formula Racional
.
21

22. 4. Métodos empíricos
4.1 Formula Racional
.
22

23. 4. Métodos empíricos
4.1 Formula Racional, ventajas y desventajas
Fórmula simple que facilita el cálculo de Q máx
Hay varias fuentes de error por variabilidad:
- Duración de la precipitación (tiempo concentración)
- Intensidad de la precipitación
- El coeficiente de escorrentía, donde se ha
simplificado la infiltración
- No se tiene en cuenta la humedad precedente suelo
23

24. 4. Métodos empíricos
4.2 Formula de Burkli - Ziegler
𝑄 = 0.022 × 𝑀 × 𝑅 × 𝐶
4 𝑆
𝑀
En donde:
Q: caudal pico [m3/s] M: Superficie de drenaje [Há]
R: Intensidad media durante la lluvia crítica [cm/h]
S: Pendiente media de la hoya [‰ tanto por mil]
C: Variable dependiente de la característica de la
superficie drenada
24

25. 4. Métodos empíricos
4.2 Formula de Burkli - Ziegler
Valores de C:
25
Tipo de Superficie C
Calles pavimentadas y barrios bastantes edificados 0.75
Calles comunes de ciudades 0.625
Poblados con plazas y calles en grava 0.3
Campos deportivos 0.25

26. 4. Métodos empíricos
4.3 Formula de Kresnik
𝑄 = 𝛼
32
0.5 +
2
𝐴
× 𝐴
En donde:
Q: caudal pico [m3/s] A: Superficie de drenaje [Km2]
a: Coeficiente variable entre 0.03 y 1.60
26

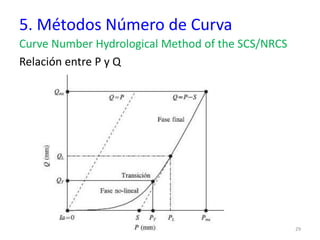
27. 5. Métodos Número de Curva
Curve Number Hydrological Method of the SCS/NRCS
El método NC establece relación empírica entre
escurrimiento directo Q[mm] y precipitación P[mm]
𝑄 =
(𝑃 − 𝐼𝑎)2
𝑃 − 𝐼𝑎 + 𝑆
Donde Ia[mm] son pérdidas iniciales: almacenamiento
superficial, intercepción vegetal, EVT, infiltración.
Ia = kS
Donde S[mm] es parámetro de retención y k=0.2 (SCS)
Reemplazando en la 1ra ecuación:
27

28. 5. Métodos Número de Curva
Curve Number Hydrological Method of the SCS/NRCS
𝑄 =
(𝑃 − 0.2𝑆)2
𝑃 + 0.8𝑆
S se estima de:
𝑆 = 25.4
1000
𝑁𝐶
− 10
Siendo 0<NC<100, suelos impermeables NC = 100
NC es función de la humedad inicial del suelo
28

29. 5. Métodos Número de Curva
Curve Number Hydrological Method of the SCS/NRCS
Relación entre P y Q
29

30. 5. Métodos Número de Curva
Curve Number Hydrological Method of the SCS/NRCS
Relación entre P y Q
30

31. 5. Métodos Número de Curva
Curve Number
.
31

32. 5. Métodos Número de Curva
Grupo hidrológico del suelo
CLASE A: Suelos de alta capacidad de infiltración.
Arenas, gravas y loess profundos.
CLASE B: Suelos de capacidad de infiltración moderada.
Loess poco profundos, marga arenosa
CLASE C: Suelos con capacidad de infiltración baja.
Marga arcillosa o arenosa poco profunda, bajo
contenido orgánico y con alto contenido de arcilla.
CLASE D: Suelos con muy baja capacidad de infiltración
o en los que el NF está cerca de la superficie. Suelos
que aumentan de volumen cuando están mojados,
arcillas plásticas pesadas y algunos suelos salinos.
32

33. 5. Métodos Número de Curva
Aplicación
Durante una tormenta se constató una precipitación
media de 12cm caída en una cuenca con una cobertura
de buenos pastos en suelos del grupo C. Estimar el
escurrimiento directo efectivo.
Solución:
De tabla SCS para buenos pastos y suelo tipo C: NC=74
Con este valor, en el gráfico relación P-Q para
P=120mm se obtiene Q=55mm
También, en formulas:
S = 89.243mm parámetro de retención
Q = 54.52mm
33

34. 5. Métodos Número de Curva
Aplicación
Una cuenca tiene NC=75 tiene un escurrimiento directo
de 40mm. Determinar el escurrimiento comparable en
una cuenca que tiene NC=85
34

35. Conclusiones
• Es necesario conocer Q máximo de avenida para
diseñar cualquier estructura hidráulica en un cauce
• Teniendo en cuenta criterios económicos y de
seguridad, debe establecerse un periodo de retorno
para cualquier obra
• Para el cálculo de Q máximo de avenida, la Fórmula
Racional es mas usada por su facilidad, sin embargo
esta asociada a incertidumbre
35

36. Trabajo Escalonado
1. Método Directo:
- Establecer tramos de cauce con condiciones que
puedan conocerse n y d (sección compuesta)
- Mediante fotografías de tramos de cauce aguas
arriba de su estaca, determinar coeficientes n
- Determinar pendiente media de la solera del cauce
- Calcular Qmáx por sección compuesta o n
equivalente
36

37. Trabajo Escalonado
2. Fórmula Racional - I:
- Usando fotografías de tramos de cauce aguas arriba
de su estaca, determinar coeficiente C ponderado
- En las curvas IDF, determinar Imáx para Tr=10 años y
duración 120 minutos (ver An. Tormenta/Sesión 6) .
Se puede usar
- Calcular Qmáx usando Área A de su Cuenca
37

38. Trabajo Escalonado
3. Fórmula Racional - II:
- Usar tablas proporcionadas
- Usar coeficiente C ponderado encontrado
- Determinar Imáx con precipitaciones de cada año,
para una duración de 4 días (96h)
- Calcular Qmáx usando Área A de sector de cuenca
Datos:
- Grupal, en hoja de cálculo
- Presentación: 16/11/2021 (21/11/2021)
38