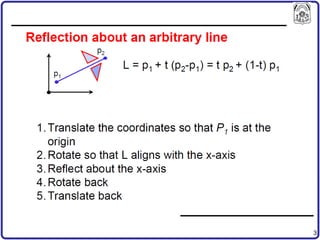
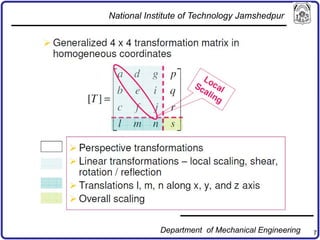
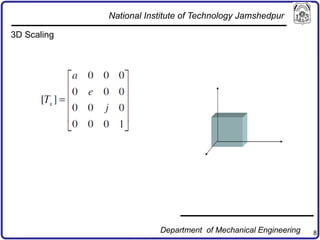
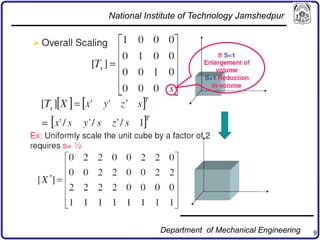
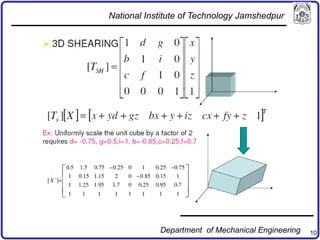
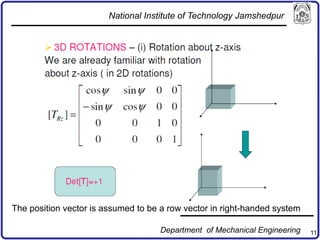
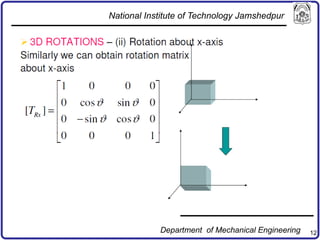
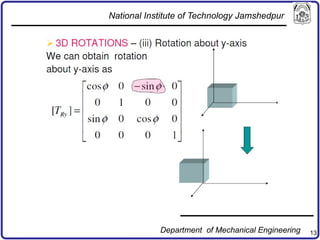
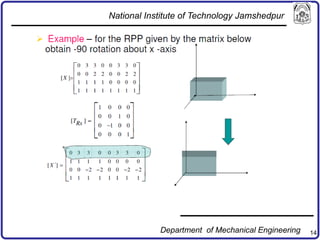
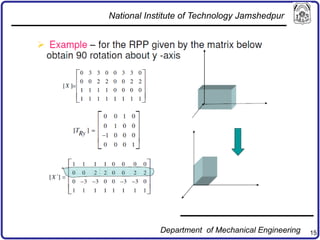
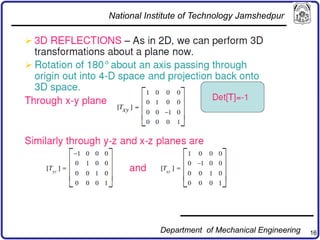
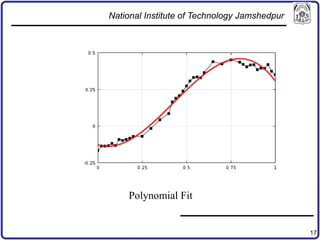
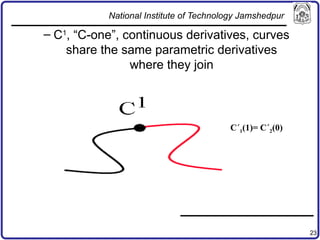
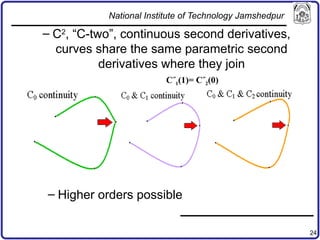
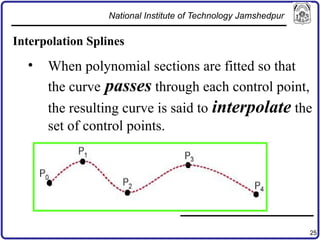
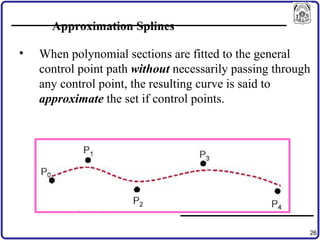
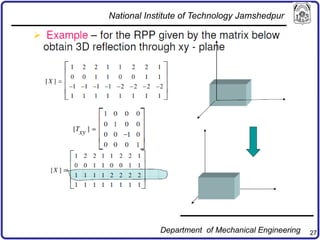
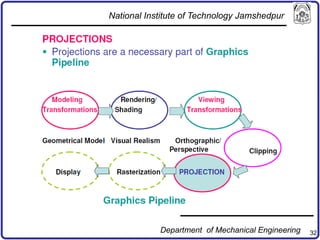
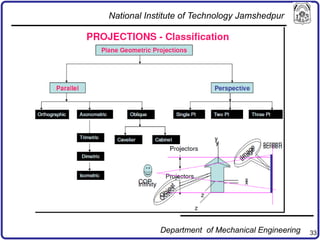
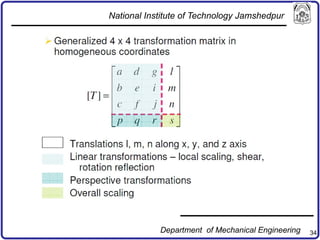
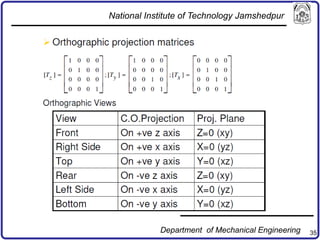
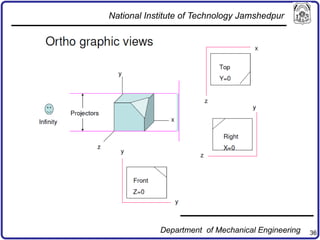
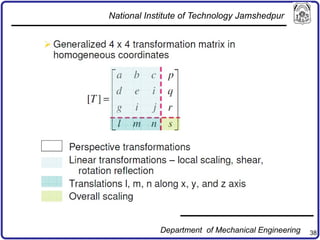
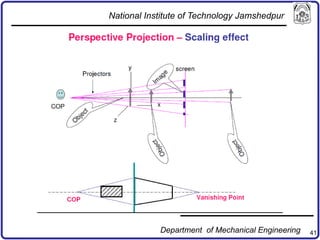
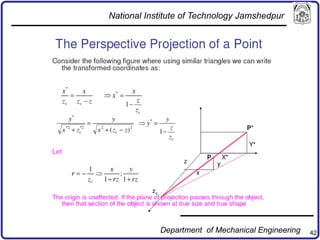
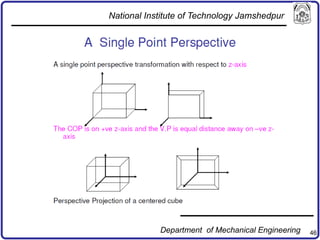
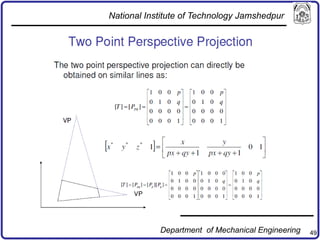
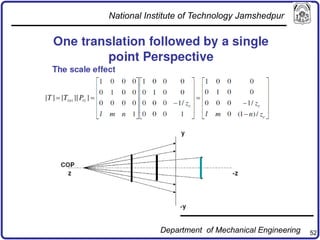
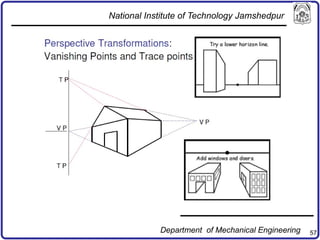
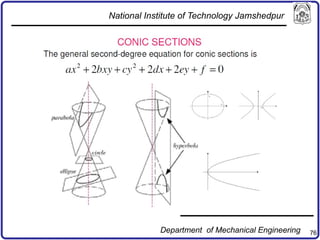
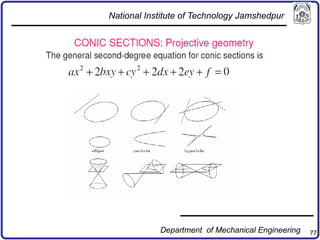
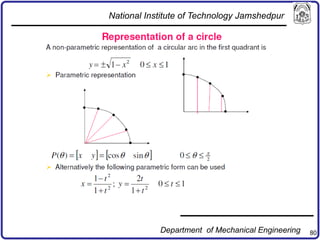
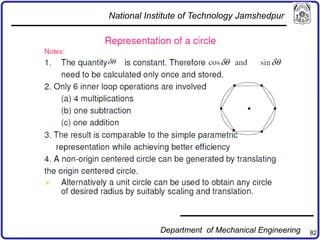
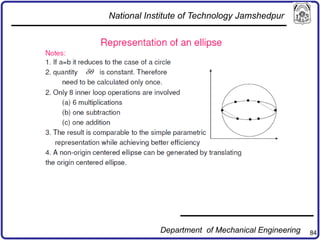
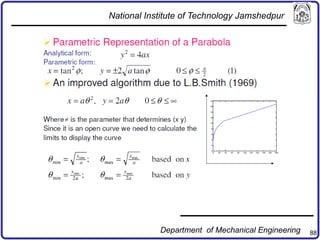
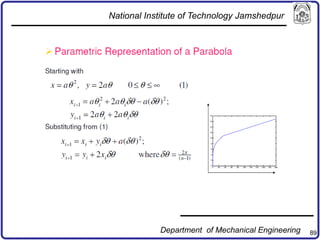
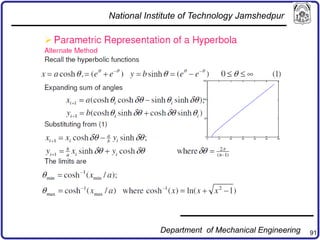
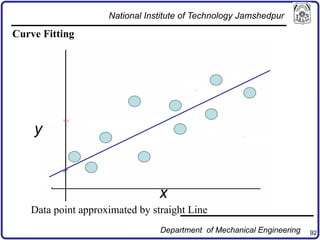
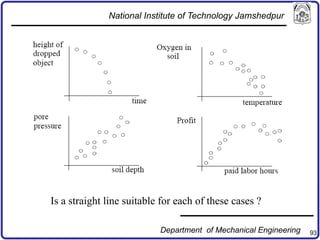
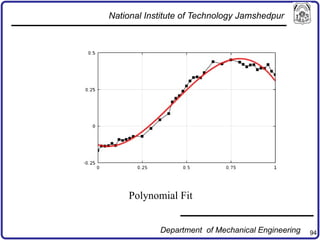
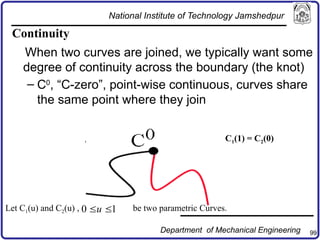
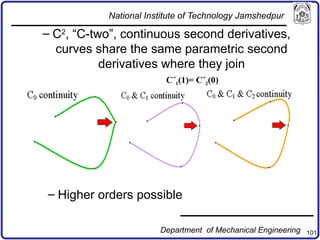
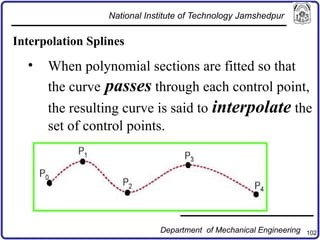
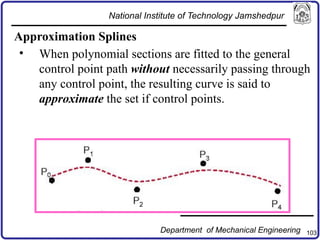
The document discusses concepts in computer-aided design and manufacturing, focusing on parametric curve representation, continuity conditions, and spline interpolation. It details different types of projections, including parallel and perspective transformations, and highlights the significance of polynomial fits in data approximation. The importance of continuity at curve junctions and the characteristics of interpolation versus approximation splines are also addressed.

1. 1
National Institute of Technology Jamshedpur
Department of Mechanical Engineering
Department of Mechanical Engineering
National Institute of Technology Jamshedpur
Deepak Kumar,
Department of Mechanical Engineering, NIT Jamshedpur
deepak.me@nitjsr.ac.in
Computer Aided Design/Computer Aided Manufacturing

2. 2
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

3. 3

4. 4

5. 5

6. 6

7. 7
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

8. 8
3D Scaling
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

9. 9
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

10. 10
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

11. 11
The position vector is assumed to be a row vector in right-handed system
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

12. 12
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

13. 13
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

14. 14
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

15. 15
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

16. 16
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

17. 17
Polynomial Fit
National Institute of Technology Jamshedpur

18. 18
National Institute of Technology Jamshedpur

19. 19
National Institute of Technology Jamshedpur

20. 20
National Institute of Technology Jamshedpur

21. 21
Parametric Continuity Conditions
• To represent a curve as a series of
piecewise parametric curves, these
curves to fit together reasonably …
Continuity!
National Institute of Technology Jamshedpur

22. 22
Continuity
When two curves are joined, we typically want some
degree of continuity across the boundary (the knot)
– C0
, “C-zero”, point-wise continuous, curves share
the same point where they join
Let C1(u) and C2(u) , be two parametric Curves.
0 1
u
 
C1(1) = C2(0)
National Institute of Technology Jamshedpur

23. 23
– C1
, “C-one”, continuous derivatives, curves
share the same parametric derivatives
where they join
C´1(1)= C´2(0)
National Institute of Technology Jamshedpur

24. 24
– C2
, “C-two”, continuous second derivatives,
curves share the same parametric second
derivatives where they join
– Higher orders possible
C˝1(1)= C˝2(0)
National Institute of Technology Jamshedpur

25. 25
Interpolation Splines
• When polynomial sections are fitted so that
the curve passes through each control point,
the resulting curve is said to interpolate the
set of control points.
National Institute of Technology Jamshedpur

26. 26
Approximation Splines
• When polynomial sections are fitted to the general
control point path without necessarily passing through
any control point, the resulting curve is said to
approximate the set if control points.

27. 27
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

28. 28
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

29. 29
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

30. 30
PROJECTIONS
1. Parallel Projections
a) Orthographic Projections
b) Axonometric Projections
2. Perspective Transformations and
Projections
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

31. 31
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

32. 32
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

33. 33
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

34. 34
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

35. 35
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

36. 36
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

37. 37
PERSPECTIVE PROJECTIONS
1. Perspective Transformations and
Projections
a) Single point
b) Two point
c) Three Point
2. Vanishing points and trace points
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

38. 38
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

39. 39
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

40. 40
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

41. 41
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

42. 42
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

43. 43
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

44. 44
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

45. 45
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

46. 46
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

47. 47
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

48. 48
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

49. 49
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

50. 50
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

51. 51
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

52. 52
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

53. 53
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

54. 54
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

55. 55
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

56. 56
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

57. 57
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

58. 58
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

59. 59
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

60. 60
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

61. 61
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

62. 62
PLANE CURVES
1. Analytical Curves
2. Synthetic Curves
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

63. 63
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

64. 64
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

65. 65
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

66. 66
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

67. 67
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

68. 68
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

69. 69
Parametric Representation of Curves and Surfaces
Two types of equations for curve representation
(1) Parametric equation x, y, z coordinates are related by a parametric variable (uor θ)
(2) Nonparametric equation x, y, z coordinates are related by a function
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

70. 70
Curve Equations
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

71. 71
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

72. 72
Parametric Equations –Advantages over nonparametric forms
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

73. 73
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

74. 74
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

75. 75
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

76. 76
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

77. 77
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

78. 78
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

79. 79
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

80. 80
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

81. 81
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

82. 82
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

83. 83
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

84. 84
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

85. 85
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

86. 86
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

87. 87
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

88. 88
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

89. 89
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

90. 90
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

91. 91
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

92. 92
y
x
Curve Fitting
Data point approximated by straight Line
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

93. 93
Is a straight line suitable for each of these cases ?
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

94. 94
Polynomial Fit
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

95. 95
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

96. 96
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

97. 97
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

98. 98
Parametric Continuity Conditions
• To represent a curve as a series of
piecewise parametric curves, these
curves to fit together reasonably …
Continuity!
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

99. 99
Continuity
When two curves are joined, we typically want some
degree of continuity across the boundary (the knot)
– C0
, “C-zero”, point-wise continuous, curves share
the same point where they join
Let C1(u) and C2(u) , be two parametric Curves.
0 1
u
 
C1(1) = C2(0)
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

100. 100
– C1
, “C-one”, continuous derivatives, curves
share the same parametric derivatives
where they join
C´1(1)= C´2(0)
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

101. 101
– C2
, “C-two”, continuous second derivatives,
curves share the same parametric second
derivatives where they join
– Higher orders possible
C˝1(1)= C˝2(0)
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

102. 102
Interpolation Splines
• When polynomial sections are fitted so that
the curve passes through each control point,
the resulting curve is said to interpolate the
set of control points.
National Institute of Technology Jamshedpur
Department of Mechanical Engineering

103. 103
Approximation Splines
• When polynomial sections are fitted to the general
control point path without necessarily passing through
any control point, the resulting curve is said to
approximate the set if control points.
National Institute of Technology Jamshedpur
Department of Mechanical Engineering