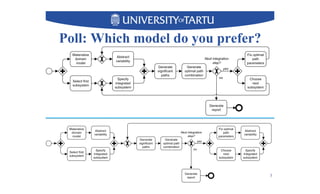
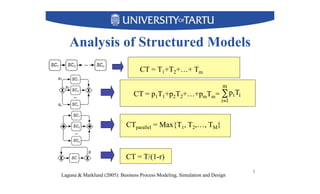
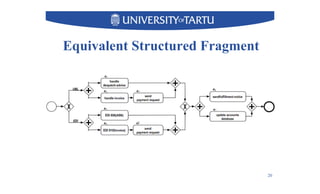
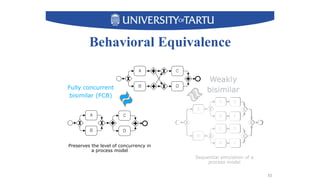
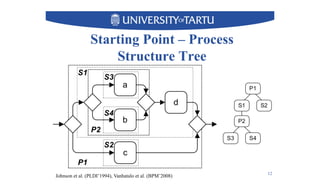
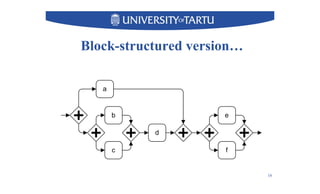
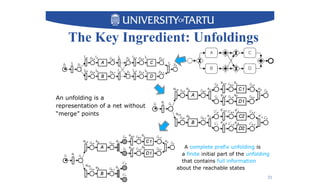
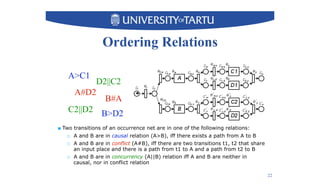
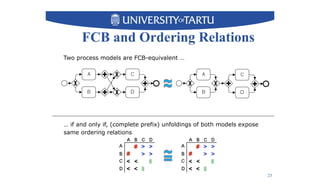
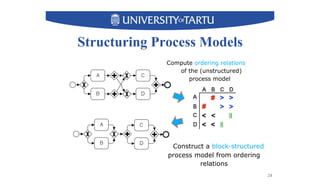
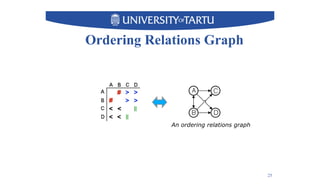
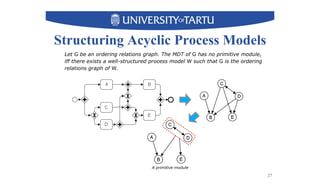
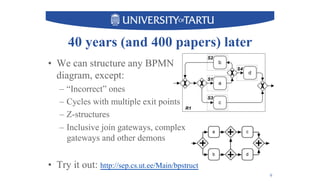
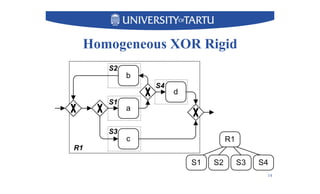
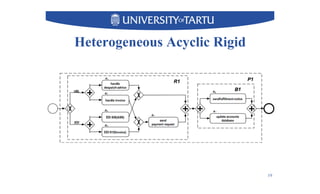
1) The document discusses techniques for determining whether a business process model can be structured and transformed into an equivalent structured model. 2) Key techniques discussed include using unfolding representations to analyze ordering relations in a model and constructing a modular decomposition tree to identify structuring opportunities. 3) The techniques can structure many common patterns but some patterns like inclusive gateways cannot be structured and remain unstructured.

1. Unraveling Unstructured Process Models
Marlon Dumas
University of Tartu, Estonia
Joint work with Artem Polyvyanyy and Luciano García-Bañuelos
Invited Talk, BPMN’2010 Workshop, Potsdam, 14 Oct. 2010

2. Poll: Which desk do you
prefer?
2

3. Poll: Which model do you prefer?
3

4. The Problem
• Premise: Structured is “better”
– Easier to understand
– Easier to analyze
– Easier to automatically layout
– Easier to abstract (zoom-out)
• We know not all models can be structured…
• Which ones can, which ones can’t?
4

5. Analysis of Structured Models
5
CTparallel = Max{T1, T2,…, TM}
CT = p1T1+p2T2+…+pmTm=
CT = T/(1-r)
CT = T1+T2+…+ Tm
Laguna & Marklund (2005): Business Process Modeling, Simulation and Design

6. Automated Layout and Abstraction
6
Wil van der Aalst et al., Process Mining Tutorial

7. A Bit of History
7
1968 1969 1970s (and 80s)

8. 20 years (and 200 papers) later…
• Everything can be structured if you accept to
break and continue
• Everyone forgot to release their implementation
(they were ashamed since it was full of GOTOs)
8

9. 40 years (and 400 papers) later
• We can structure any BPMN
diagram, except:
– “Incorrect” ones
– Cycles with multiple exit points
– Z-structures
– Inclusive join gateways, complex
gateways and other demons
• Try it out: http://sep.cs.ut.ee/Main/bpstruct
9

10. Corollary (if you care)
• Any (sound) BPMN model can be
transformed into an equivalent (readable)
BPEL process definition
10
• If BPEL had break/continue statements or we use boolean variables to simulate break/continue statememts
• And the BPMN model does not have inclusive join gateways, complex gateways and other demons
• And some other minor details not worth mentioning

11. 11
Behavioral Equivalence
Preserves the level of concurrency in
a process model
Sequential simulation of a
process model
Fully concurrent
bisimilar (FCB)
Weakly
bisimilar
Weakly
bisimilar
Sequential simulation of a
process model

12. Starting Point – Process
Structure Tree
12
Johnson et al. (PLDI’1994), Vanhatalo et al. (BPM’2008)

13. 13
Taxonomy of Process Fragments
■ Trivials, polygons, and bonds are structured fragments
■ Rigids are “unstructured”
13

14. Homogeneous XOR Rigid
14

15. Homogeneous AND Rigid
15

16. Block-structured version…
16

17. Homogeneous AND Rigid that
cannot be structured
• Causal rules:
– {A, B}  { C }
– { B }  { D }
• Overlap on the left-hand side of the rules

18. Compare to this…
• Causal relations
– {A, B}  {C, D}

19. Heterogeneous Acyclic Rigid
19

20. Equivalent Structured Fragment
20

21. The Key Ingredient: Unfoldings
An unfolding is a
representation of a net without
“merge” points
A complete prefix unfolding is
a finite initial part of the unfolding
that contains full information
about the reachable states
21

22. Ordering Relations
■ Two transitions of an occurrence net are in one of the following relations:
□ A and B are in causal relation (A>B), iff there exists a path from A to B
□ A and B are in conflict (A#B), iff there are two transitions t1, t2 that share
an input place and there is a path from t1 to A and a path from t2 to B
□ A and B are in concurrency (A||B) relation iff A and B are neither in
causal, nor in conflict relation
A>C1
B>D2
B#A
A#D2
C2||D2
D2||C2
22

23. FCB and Ordering Relations
Two process models are FCB-equivalent …
… if and only if, (complete prefix) unfoldings of both models expose
same ordering relations
23

24. Structuring Process Models
Compute ordering relations
of the (unstructured)
process model
Construct a block-structured
process model from ordering
relations
24

25. Ordering Relations Graph
An ordering relations graph
25

26. Modular Decomposition Tree (MDT)
 The MDT is unique and can be computed in linear time
The MDT
■ A linear (L) module is a total order on a set of nodes of a graph
■ A complete (C) module is a complete graph, or a clique
■ A primitive (P) module is neither trivial, nor linear, nor complete
 A module is a set of edges with uniform structure
26

27. 27
Structuring Acyclic Process Models
A primitive module
Let G be an ordering relations graph. The MDT of G has no primitive module,
iff there exists a well-structured process model W such that G is the ordering
relations graph of W.

28. Heterogeneous Cyclic Rigid
28

29. For further details…
Download and try:
• http://sep.cs.ut.ee/Main/bpstruct
• http://code.google.com/p/bpstruct/
Perspectives:
• Analyze
• Decompose (e.g. for distributed execution)
• Refactor (extract duplicate fragments into subprocesses)
• Visualize
29