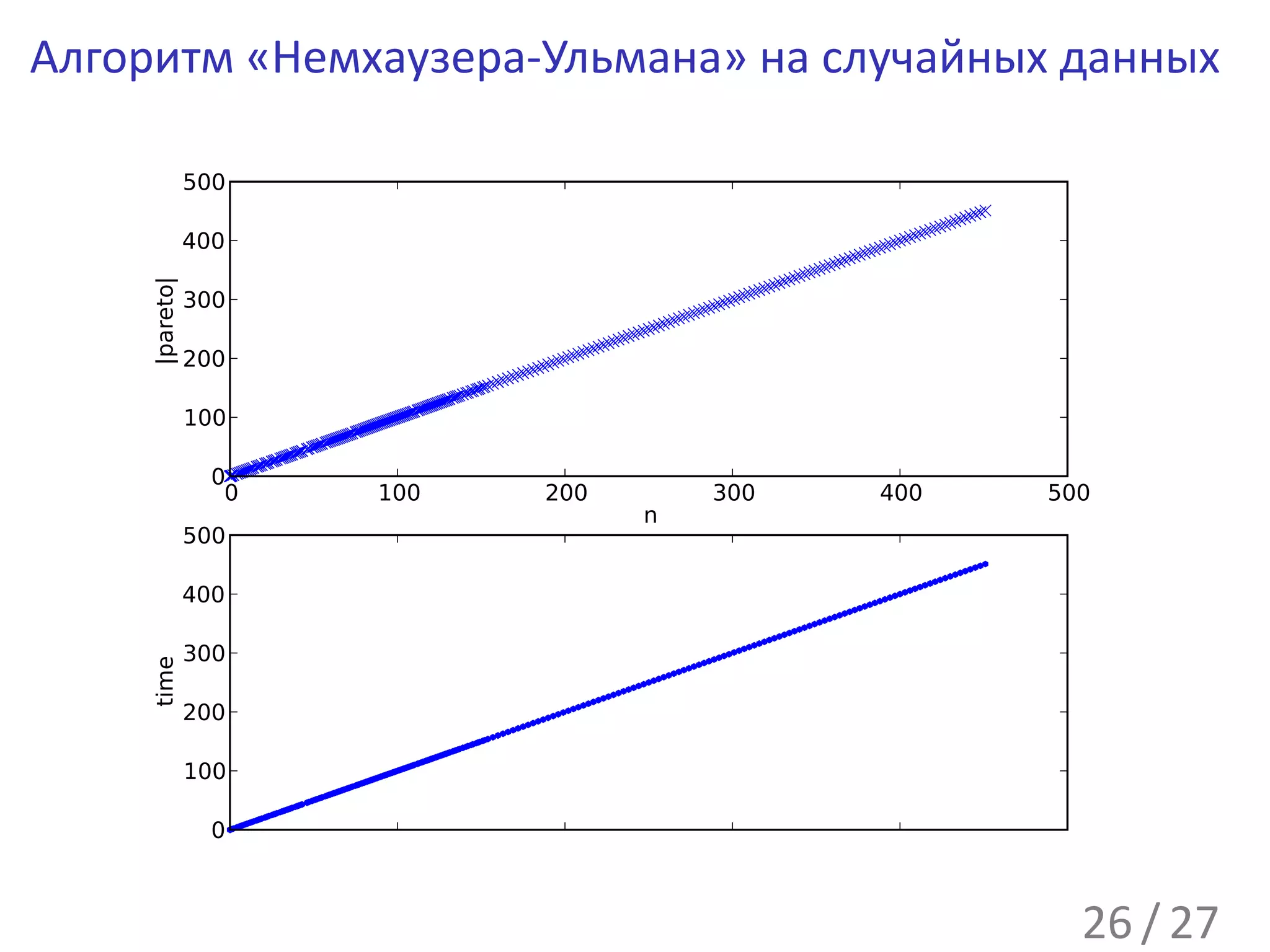
Документ описывает полиномиальный в среднем алгоритм для задачи о рюкзаке, основываясь на работах других исследователей. Обсуждаются определения и характеристики парето-оптимальных решений, а также представляются алгоритмы, включая алгоритм Немхаузера-Ульмана для нахождения оптимальных решений. Рассматривается также математическое ожидание сложности алгоритма и влияние на него различных факторов, таких как распределение стоимостей и весов.

1. @safe@act @safe@act
1 / 27

2. Полиномиальный в среднем алгоритм для
«Рюкзака»
Н. Н. Кузюрин С. А. Фомин
24 июня 2010 г.
Лекция основана на результатах из: «Beier,
Δ>0
R. and Vöcking, B. (2003). In Proceedings of
стоимости наборов
Δ>0
the 35th ACM Symposium on Theory of
Δ<0
Δ<0
Δ>0
Compu ng (STOC), pages 232–241».
все наборы в порядке возрастания весов
2 / 27

3. .
Определение .
..
«Полиномиальный в среднем (точно)»
Алгоритм A называется полиномиальным в среднем, если среднее
время его работы ограничено полиномом от длины входа, т. е.
. ∃C > 0 : En TA = O(nC ).
.. .
.
.
Упражнение .
..
Найдите TA , время работы некоторого A, и входное распределение Pn (I),
что En TA = O(nC ), но En T2 ̸= O(nC ).
. A
.. .
.
.
Определение .
..
«Полиномиальный в среднем»
Алгоритм называется полиномиальным в среднем, если для времени
работы алгоритма T выполняется:
. ∃ε > 0 : En Tε = O(n).
.. .
.
3 / 27

4. Задача о рюкзаке
.
Задача .
..
«0–1 Рюкзак (Knapsack)»
Даны:
c1 , . . . , cn , cj ∈ N — «стоимости» предметов;
a1 , . . . , an , aj ∈ N — «размеры» или «веса»;
B ∈ N — «размер рюкзака».
Найти максимальное значение f∗ целевой функции
∑
n
f≡ ci xi → max
i=1
с ограничением на размер «рюкзака»:
∑
n
ai xi ≤ B, xi ∈ {0, 1}.
. i=1
.. .
.
4 / 27

5. 5 / 27

6. Парето-оптимальные решения
.
Определение .
..
Пусть S1 и S2 допустимые подмножества предметов для
задачи «Knapsack». S1 доминирует над S2 , если:
стоимость S1 больше стоимости S2 ,
. вес S1 не больше веса S2 .
.. .
.
т. е. набор доминирующих подмножеств есть набор
Парето-оптимальных решений, т. е. таких решений, в которых нельзя
улучшить один параметр (стоимость), без ухудшения другого параметра
(увеличения веса).
6 / 27

7. Алгоритм Немхаузера – Ульмана
def KnapsackNemhauserUllman(items, B):
pareto = [ ItemSet() ] # Парето-оптимальные по весу
for item in items:
news=[]
for solution in pareto:
if solution.weight + item.weight <= B:
news.append(solution + item)
mergedItemSet = merge_item_sets(pareto, news)
pareto = mergedItemSet
return pareto[-1], len(pareto)
7 / 27

8. Алгоритм Немхаузера – Ульмана
Предметы ( стоимость ): [ 6 , 3 , 2 , 3 , 6 ], B = 10
вес 3 4 5
3
8
pareto news mergedItemSet
[0]
0 [6]
3 [0, 3]
0
6
[0, 6]
0 3 [3, 9]
4 7 [0, 3, 9]
0
6
7
[0, 6, 9]
0 3 7 [2, 8]
5 8 [0, 3, 9]
0
6
7
[0, 6, 9]
0 3 7 [3, 9,
3 6
12
10 ] [0, 3, 9,
0
6
6
12
10 ]
[0, 6, 9,
0 3 6
12
10 ] [6]
8 [ 0 , 3 , 9 , 12 ]
0
6
6 10
12
Оптимальное решение: 10
8 / 27

9. Алгоритм Немхаузера – Ульмана
def KnapsackNemhauserUllman(items, B):
pareto = [ ItemSet() ] # Парето-оптимальные по весу
for item in items:
news=[]
for solution in pareto:
if solution.weight + item.weight <= B:
news.append(solution + item)
mergedItemSet = merge_item_sets(pareto, news)
pareto = mergedItemSet
return pareto[-1], len(pareto)
Сложность алгоритма — O(n · |ParetoSolu ons|).
9 / 27

10. Мат. ожидание сложности алгоритма полиномиально
.
Теорема .
..
Пусть:
ai — «веса», произвольные положительные числа;
ci — «стоимости», независимые случайные величины,
равномерно распределенные на [0, 1];
q = max |ParetoSolutions| — число доминирующих подмножеств для
всех n предметов.
Тогда
. E(q) = O(n3 ).
.. .
.
10 / 27

11. Определения
m = 2n
S1 , . . . , Sm — подмножества [n] в порядке неубывания весов.
∑
Сами веса i∈Sk ai множеств Sk в нашей теме не возникают.
11 / 27

12. Δ>0
стоимости наборов
Δ>0
Δ<0
Δ<0
Δ>0
все наборы в порядке возрастания весов
Для любых 2 ≤ u ≤ m, 1 ≤ k ≤ u:
Plusk = Su Sk Minusk = Sk Su
∑ ∑
∆+ =
k ci ∆− =
k ci
i∈Plusk i∈Minusk
∆u = min ∆+ − ∆−
k k
1≤k<u
∀u ≥ 2, Su — доминирующее множество ⇔ ∆u > 0.
12 / 27

13. Δ>0
стоимости наборов
Δ>0
Δ<0
Δ<0
Δ>0
все наборы в порядке возрастания весов
Стоимость Sm ≤ n
В среднем: чем больше ∆u > 0 для каждого доминирующего
набора u → тем меньше q.
13 / 27

14. План
Δ>0
стоимости наборов
Δ>0
Δ<0
Δ<0
Δ>0
все наборы в порядке возрастания весов
...
1 оценим вероятность «неблагоприятных» событий: небольшой
прирост ∆u > 0;
...
2 найдем E ∆u > 0;
...
3 оценим E q = E |ParetoSolutions|.
14 / 27

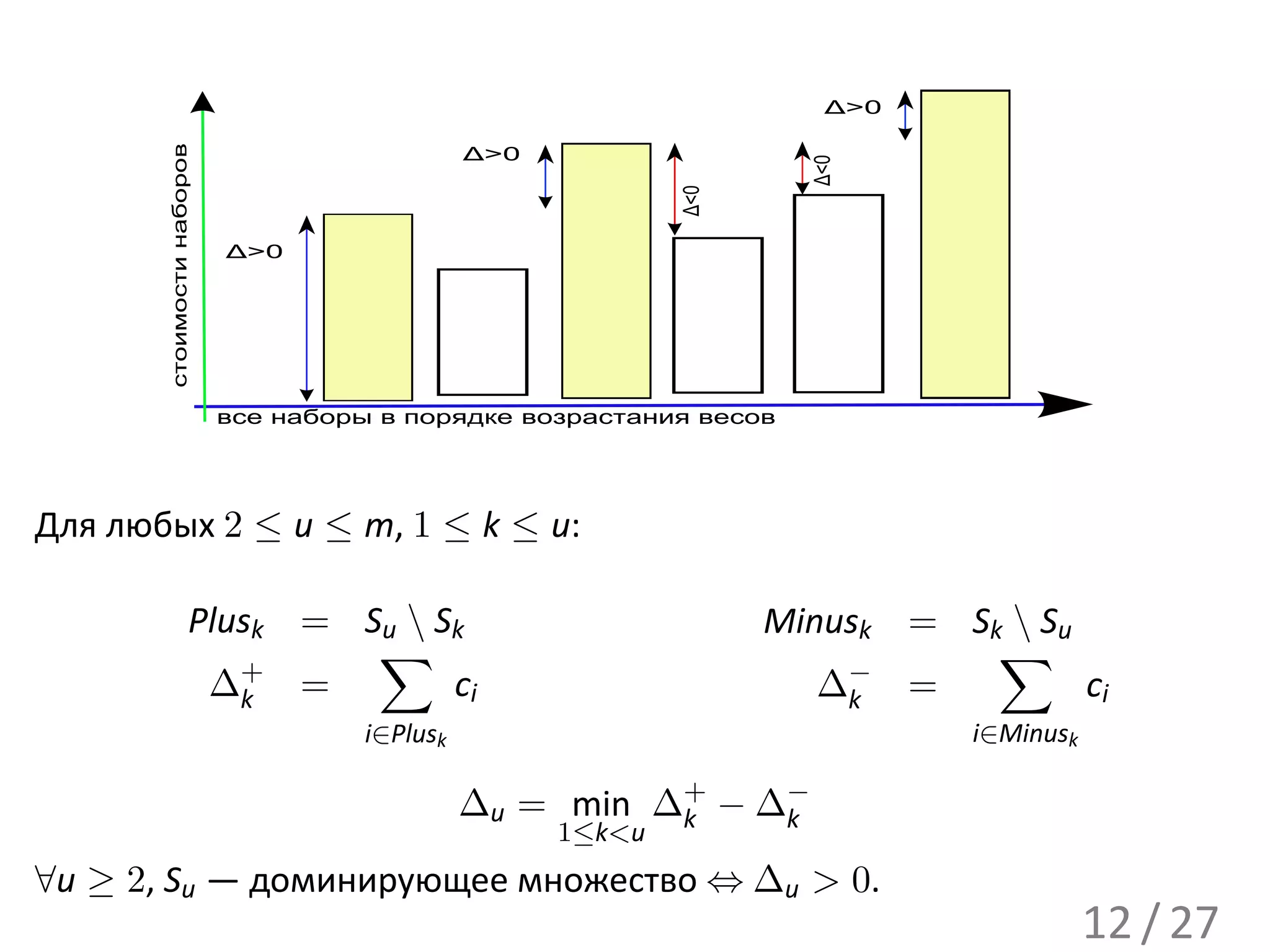
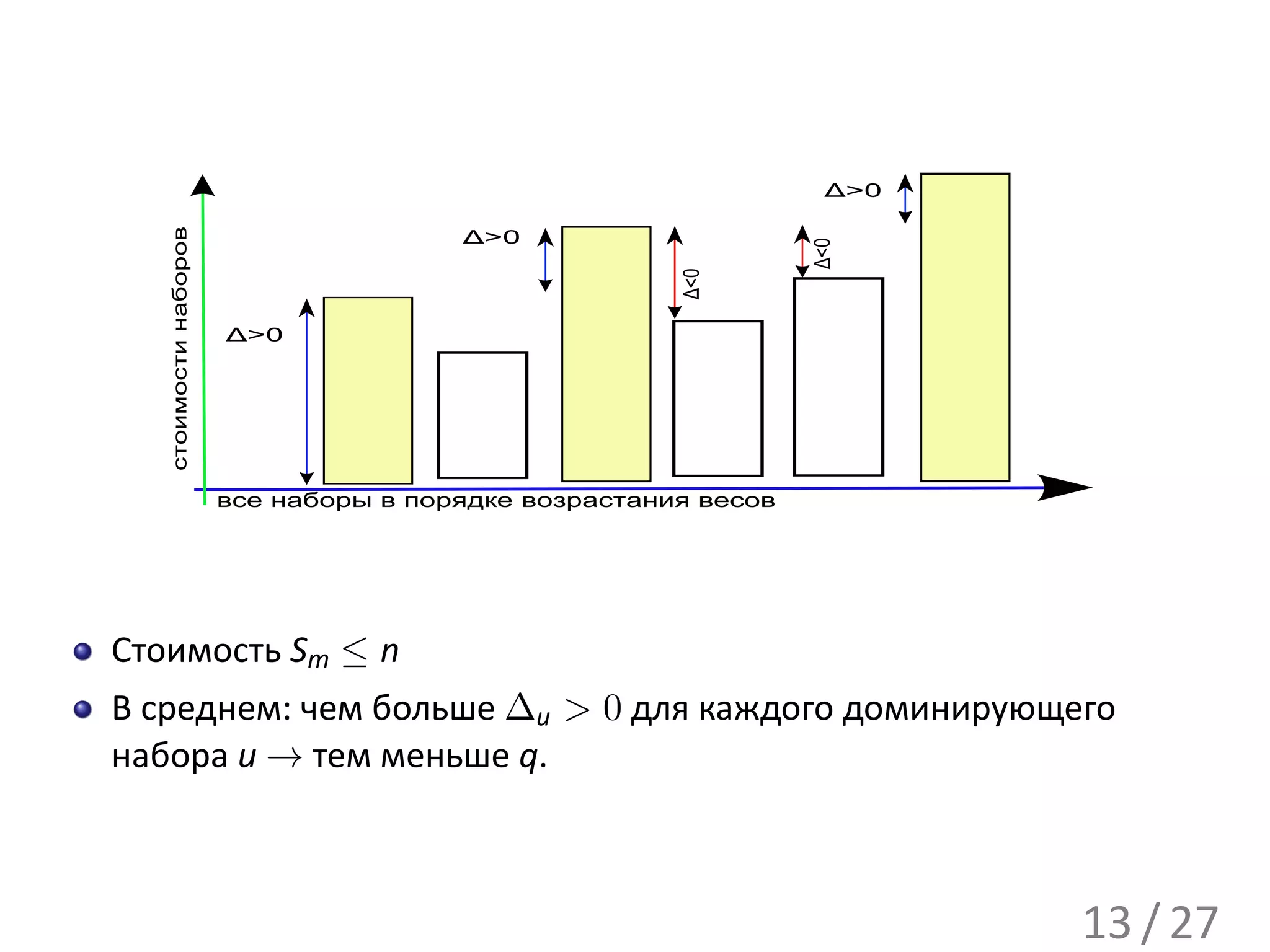
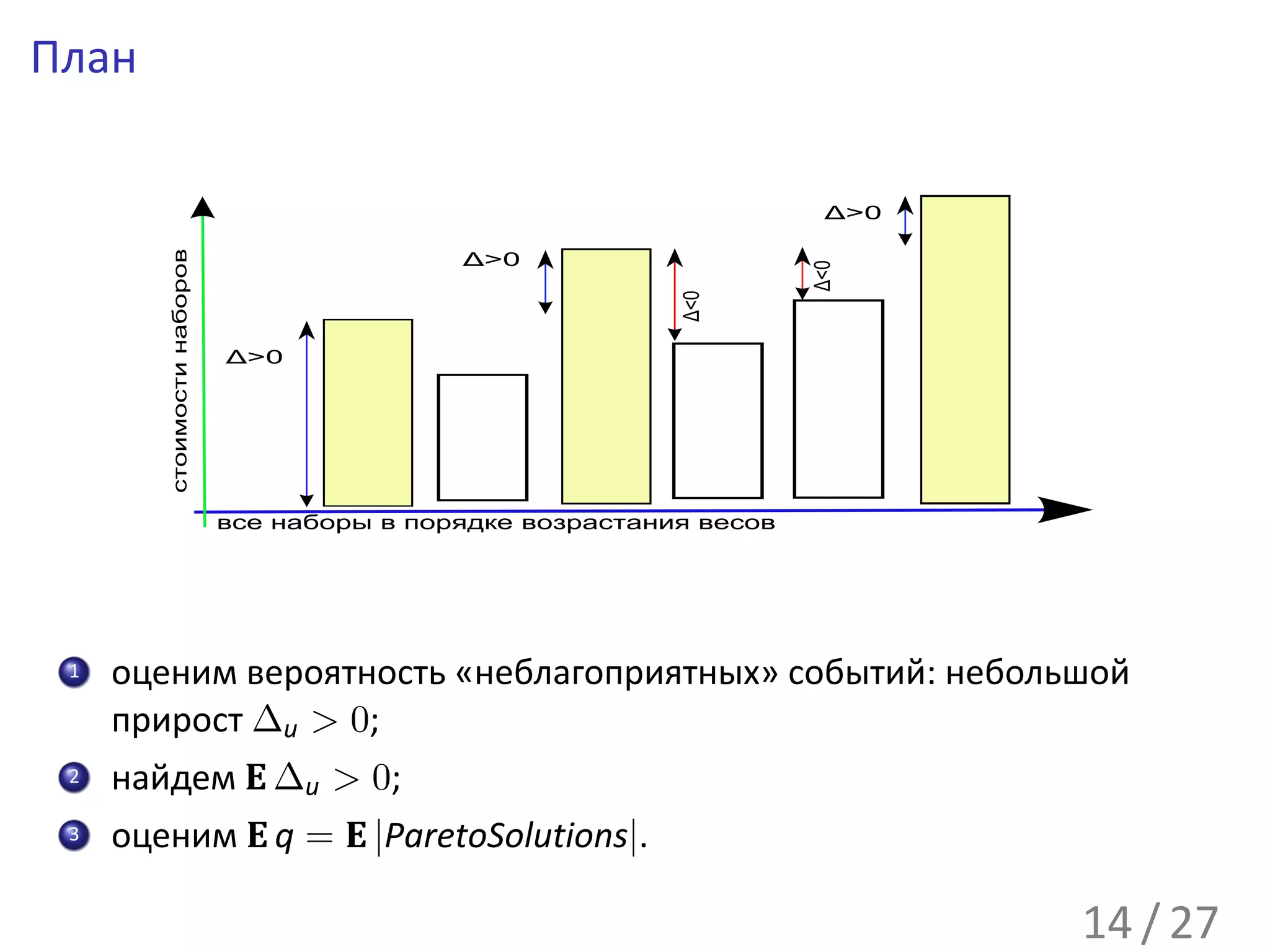
15. Некоторое u ≥ 2.
Пусть Su = [1, . . . , t] (иначе перенумеруем).
∀ 1 ≤ k < u Plusk ⊆ [1, . . . , t], Minusk ⊆ [t + 1, . . . , n]
Пусть 0 < ε < 1.
.
События .
..
ПаретоНабор = {∆u > 0}
{ }
ДельтаМала = ∆u < ε2
ЭлементМалj = {cj < ε}
ЭлементНеМалj = ЭлементМалj= {cj ≥ ε}
t
ВНабореНеМалы = ∩j=1 ЭлементНеМалj
.
.. .
.
15 / 27

16. Детальный план
16 / 27

17. P(ВНабореНеМалы|ПаретоНабор) ≤ nε
∀j ≤ t и 0 < ε < 1:
)
P (cj < ε| ∀k : ∆+ > ∆−
k k = P (cj < ε| cj > x)
{
при x ≥ ε: 0
≤ ε(1−x) x(1−ε)
ε−x
при x < ε: 1−x = 1−x − 1−x
≤ ε
P(cj < ε|cj > x)
-
0 x ε 1
P(ВНабореНеМалы|ПаретоНабор) = P(∪t ЭлементМалj |ПаретоНабор)
j=1
∑
t
≤ P(ЭлементМалj |ПаретоНабор)
j=1
≤ t · ε ≤ nε.
17 / 27

18. Детальный план
18 / 27

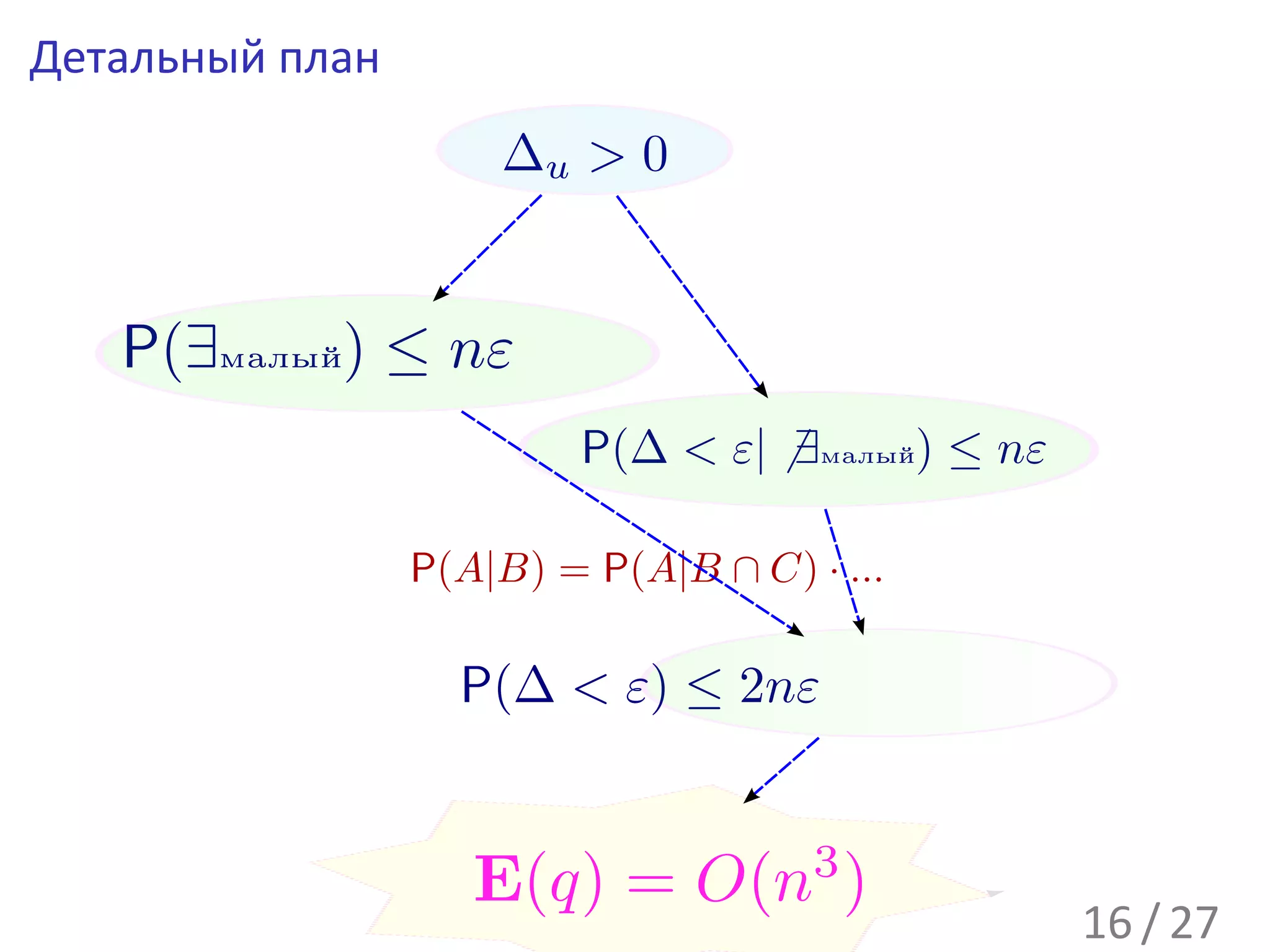
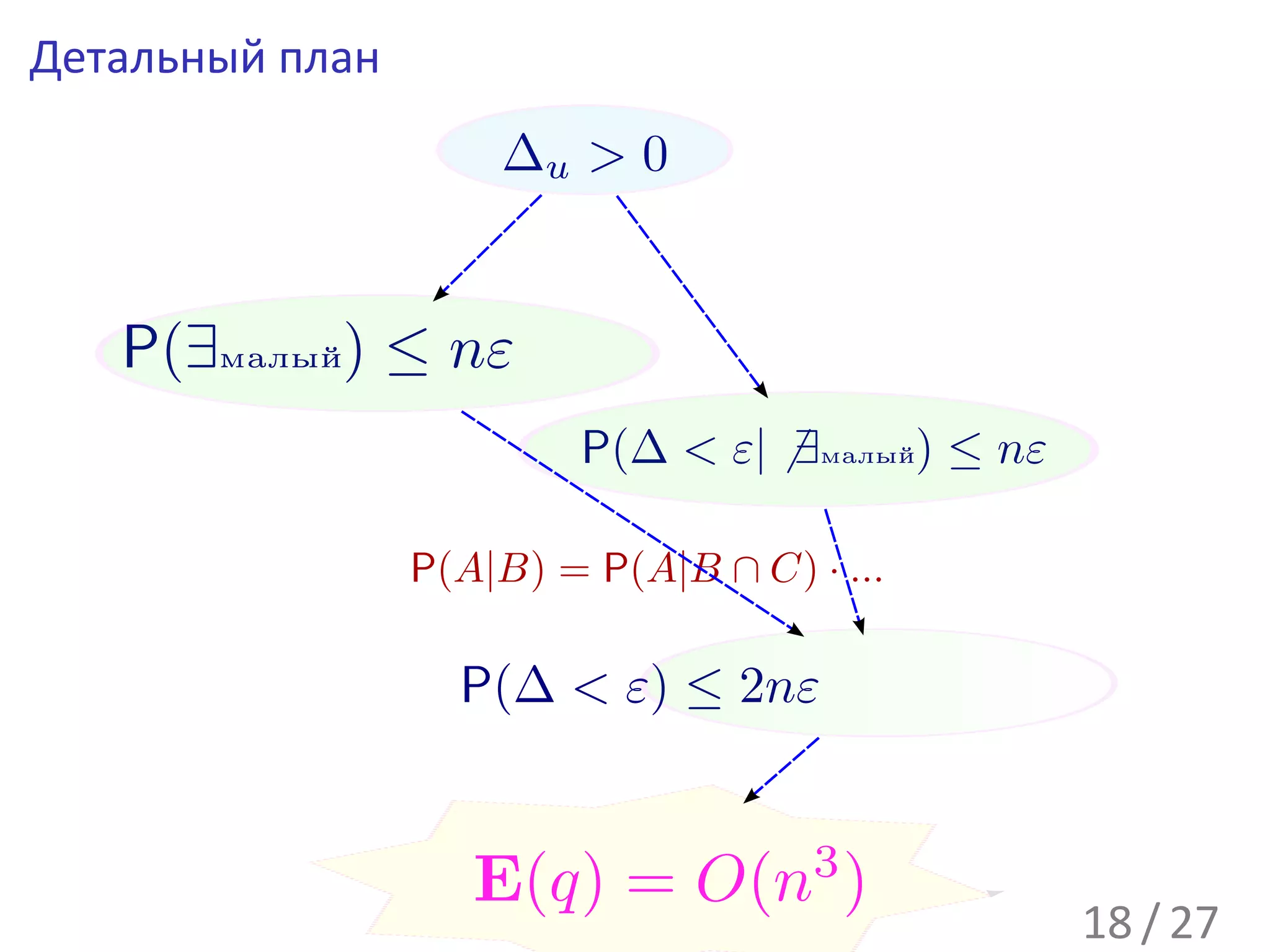
19. P(ДельтаМала|ПаретоНабор ∧ ВНабореНеМалы) ≤ nε
Оценим P(ПаретоНабор) при априорности событий (при условии):
«∀j cj ∈ [0, 1]», «ВНабореНеМалы» (и, следовательно, «∆+ ≥ ε»):
k
( )
P(ПаретоНабор|ВНабореНеМалы) = P ∀k ∆− ≤ ∆+ , ∀j > t cj ∈ [0, 1] =
k k
1 ( )
= P ∀k ∆− ≤ (1 − ε) ∆+ , ∀j > t cj ∈ [0, 1 − ε] ≤
(1 − ε) n−t k k
1 ( )
≤ P ∀k ∆− ≤ ∆+ − ε2 , ∀j > t cj ∈ [0, 1 − ε] ≤
(1 − ε) n−t k k
1
≤ P (ДельтаМала|ВНабореНеМалы)
(1 − ε)n−t
С другой стороны, ДельтаМала ⊂ ПаретоНабор, и
P(ДельтаМала|ПаретоНабор ∧ ВНабореНеМалы) =
P(ДельтаМала|ВНабореНеМалы)
= ≥ (1 − ε)n−t ≥ (1 − ε)n ≥ 1 − nε
P(ПаретоНабор|ВНабореНеМалы)
19 / 27

20. Детальный план
20 / 27

21. P(A|B) = P(A|B ∩ C) · P(C|B) + P(A|B ∩ C) · P(C|B)
x+y
P(A|B) =
x+y+z+w
событие A
событие C
P(A|B ∩ C) · P(C|B) =
y y y+z
= ·
x z y+z x+y+z+w
w
P(A|B ∩ C) · P(C|B) =
событие B
x x+w
= ·
x+w x+y+z+w
21 / 27

22. Детальный план
22 / 27

23. P(ДельтаМала|ПаретоНабор) ≤ 2nε
P(A|B) = P(A|B ∩ C) · P(C|B) + P(A|B ∩ C) · P(C|B)
Оценим P(ДельтаМала|ПаретоНабор):
P(ДельтаМала|ПаретоНабор) =
= P(ДельтаМала|ПаретоНабор ∩ ВНабореНеМалы) · P(ВНабореНеМалы|ПаретоНабор)
+ P(ДельтаМала|ПаретоНабор ∩ ВНабореНеМалы) · P(ВНабореНеМалы|ПаретоНабор)
≤ P(ДельтаМала|ПаретоНабор ∩ ВНабореНеМалы) + P(ВНабореНеМалы|ПаретоНабор)
≤ nε + nε = 2nε
23 / 27

24. Детальный план
24 / 27

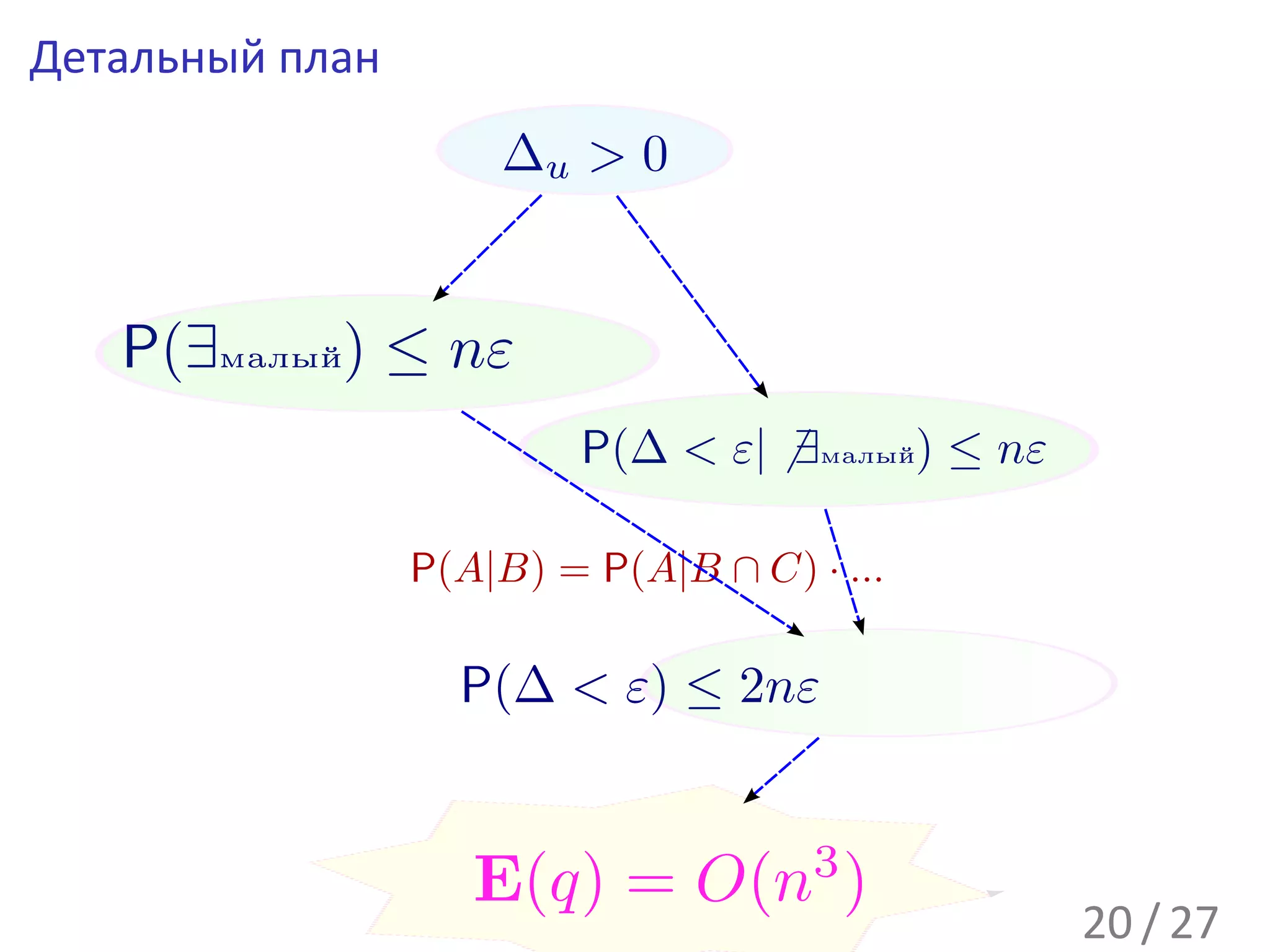
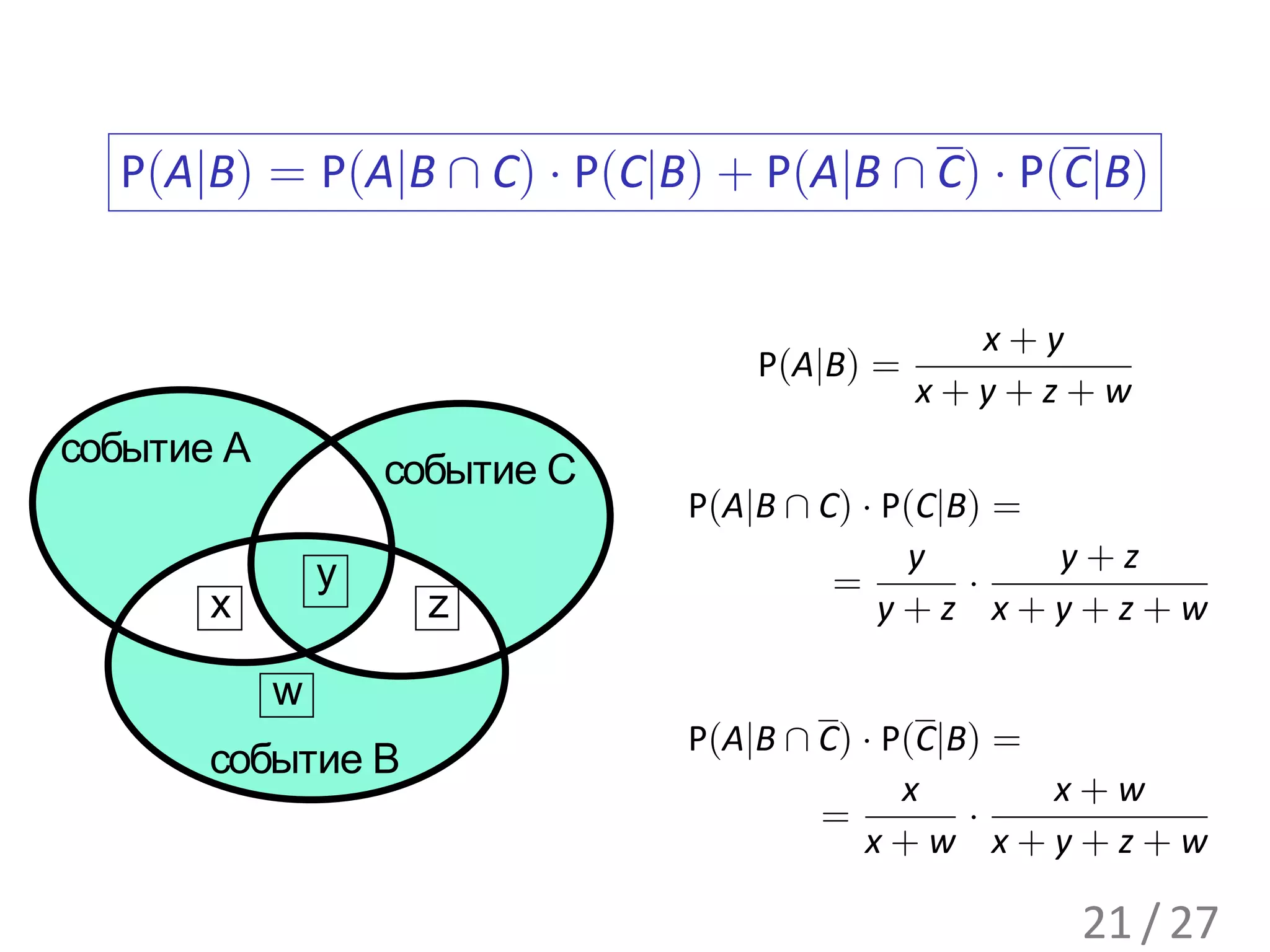
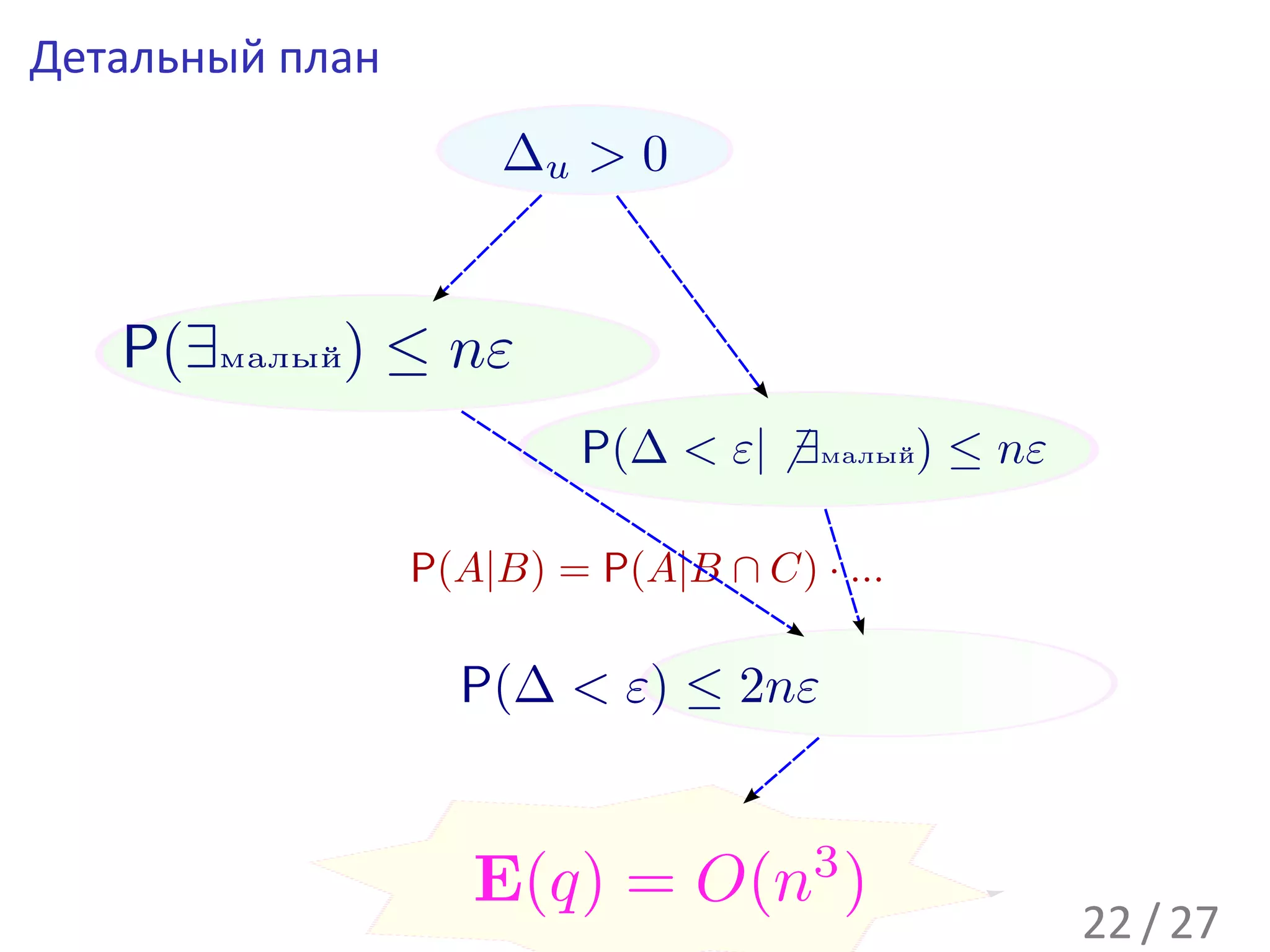
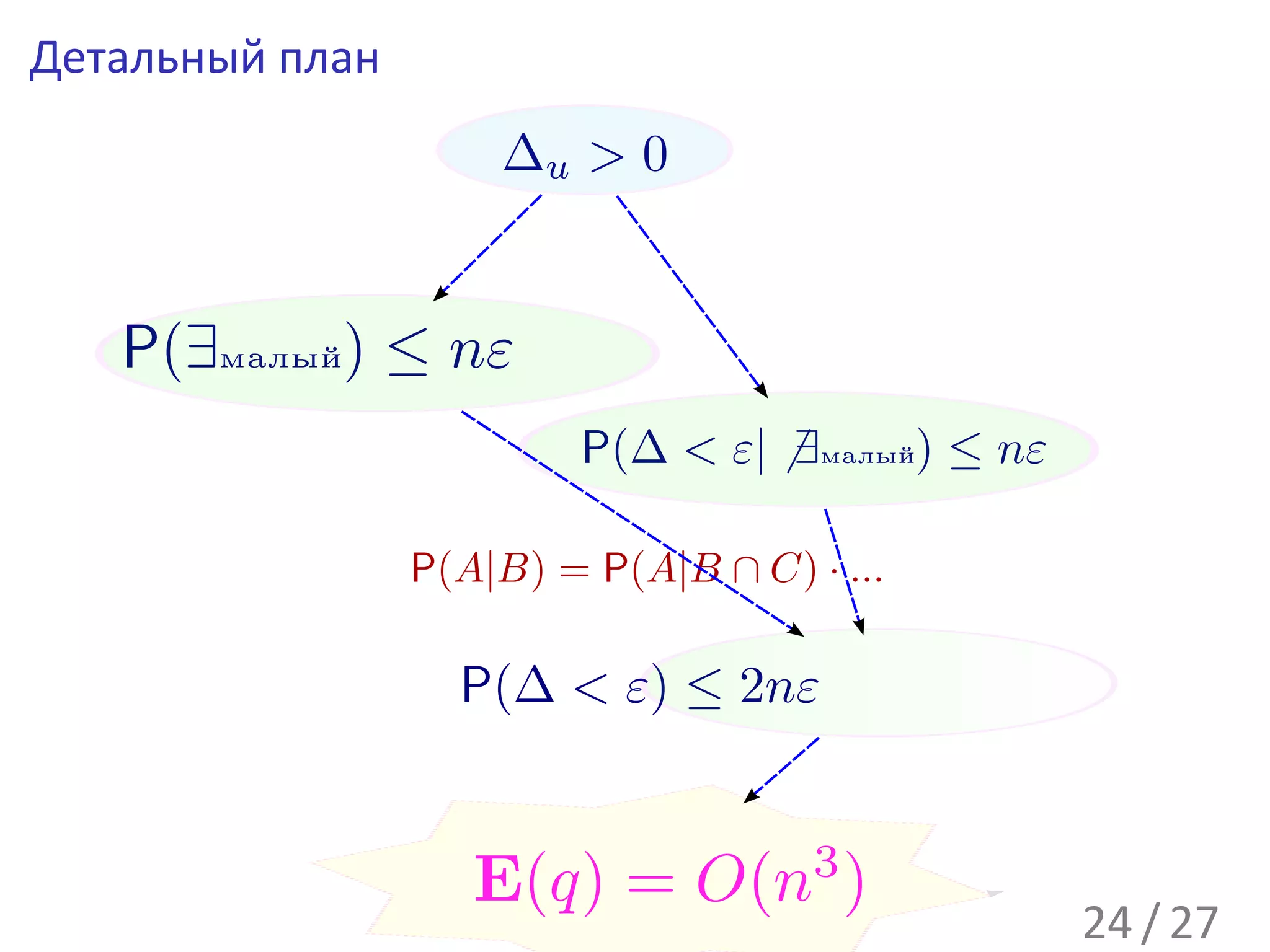
25. E(q) = O(n3 )
1
Возьмем ε = 3n , тогда
E(∆u |∆u > 0) ≥ ε2 · P(∆u > ε2 |ПаретоНабор)
= ε2 · (1 − P[ДельтаМала|ПаретоНабор])
( )
1 2 1
≥ ε · (1 − 2nε) = 2 · 1 −
2
=
9n 3 27n2
Обозначим мат. ожидание стоимости Sm через Cm . Имеем две оценки:
{
n · E(c ) = 2
n
Cm = ∑m i 1 ∑m
u=2 P(∆u > 0) E(∆u |∆u > 0) ≥ 27n2 u=2 P(∆u > 0)
∑
m
n
E(q) = 1 + P(∆u > 0) ≤ 1 + · 27n2 = O(n3 )
2
u=2
25 / 27

26. Алгоритм «Немхаузера-Ульмана» на случайных данных
26 / 27

27. Интернет поддержка курса
.
.
http://discopal.ispras.ru/
.
.. .
.
.
Вопросы?
.
.. .
.
.
27 / 27