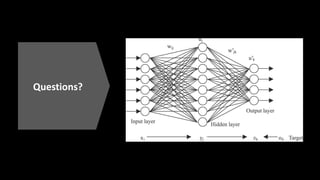
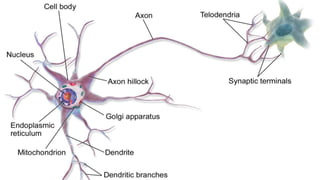
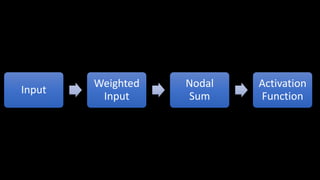
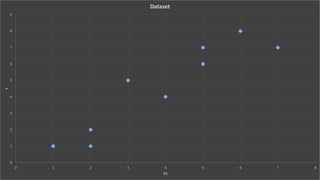
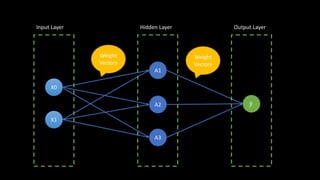
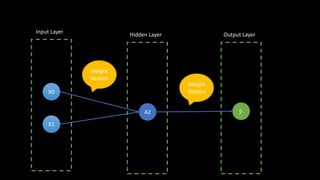
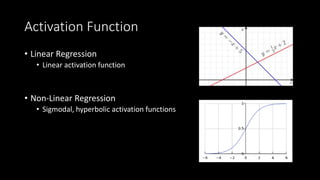
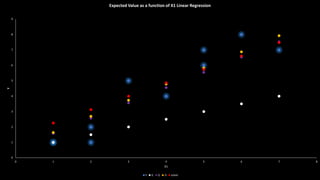
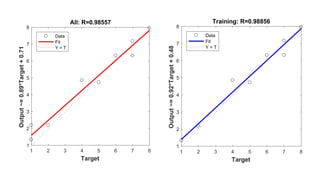
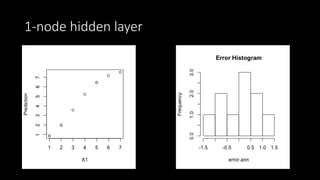
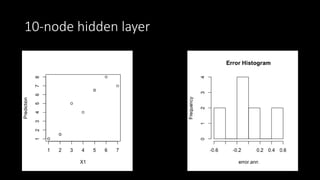
This document discusses neural networks and regression using artificial neural networks. It describes how neural networks mimic the human brain with networks of neurons and weighted connections. The document outlines the basic structure of a neural network with an input layer, hidden layers, and an output layer. It also discusses different activation functions that can be used for linear or nonlinear regression. The document provides an example of using an artificial neural network for regression with R code. It discusses concepts like forward and backward propagation, gradient descent, and minimizing a cost function.

1. Neural Network
Regression
By: Zhanyi Zhou

2. Artificial Neural
Network
• Human brain has
about 100 billion
neurons
• Machine learning
technique that mimics
the way humans solve
problems

4. Input
Weighted
Input
Nodal
Sum
Activation
Function

5. 0
1
2
3
4
5
6
7
8
9
0 1 2 3 4 5 6 7 8
Y
X1
Dataset

6. X0
X1
Input Layer
A2
A1
A3
Hidden Layer
𝑦
Output Layer
Weight
Vectors
Weight
Vectors

7. A2
Hidden Layer
𝑦
Output Layer
X0
X1
Input Layer
Weight
Vectors
Weight
Vectors

8. Activation Function
• Linear Regression
• Linear activation function
• Non-Linear Regression
• Sigmodal, hyperbolic activation functions

9. 0
1
2
3
4
5
6
7
8
9
0 1 2 3 4 5 6 7 8
Y
X1
Expected Value as a function of X1 Linear Regression
Y i1 i2 i3 solver

10. 1 2 3 4 5 6 7 8
Target
1
2
3
4
5
6
7
8
Output~=0.89*Target+0.71 All: R=0.98557
Data
Fit
Y = T
1 2 3 4 5 6 7 8
Target
1
2
3
4
5
6
7
8
Output~=0.92*Target+0.48
Training: R=0.98856
Data
Fit
Y = T

11. library(nnet)
library(randomForest)
model.abc<-nnet(mlr_OG$X1, mlr_OG$Y, size=10, linout = TRUE)
plot(mlr_OG$X1,predict(model.abc), ylab="Prediction", xlab="X1")
error.ann=mlr_OG$Y-predict(model.abc)
hist(error.ann, main="Error Histogram" )
R-Code

12. 1-node hidden layer

13. 10-node hidden layer

14. Algorithm and Methods
• Forward and Backward Propagation(supervised learning)
• Gradient descent algorithm
• Stochastic, batch, mini-batch
• Minimize the cost function

15. 𝐸 =
1
2
( 𝑦 − 𝑦)2
𝐽1 =
𝒅𝑬
𝒅𝑾
=
𝑑𝑬
𝑑 𝑦
𝑑 𝑦
𝑑𝑧
𝑑𝑧
𝑑𝑾
= ( 𝑦 − 𝑦)
−𝑒−𝑧
1+𝑒−𝑧 2 [
𝜕𝑍
𝜕𝑊
(𝑥0 𝑤0 + 𝑥1 𝑤1 + 𝑥2 𝑤2)]
J2 =
𝒅𝑬
𝒅𝑾
=
𝑑𝑬
𝑑 𝑦
𝑑 𝑦
𝑑𝑧
𝑑𝑧
𝑑𝑾
= ( 𝑦 − 𝑦)[
𝜕𝑍
𝜕𝑊
(𝑥𝑖 𝑤𝑖 + 𝑥𝑗 𝑤𝑗 + 𝑥 𝑘 𝑤 𝑘)]

17. Questions?