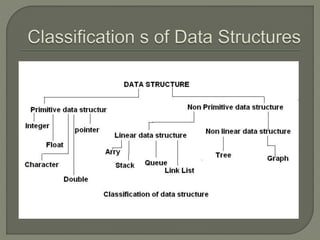
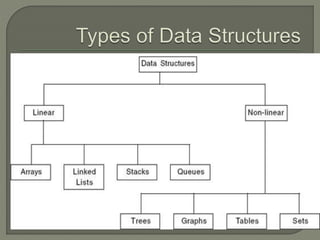
The document discusses arrays in C programming. It defines arrays as a collection of similar data types stored in contiguous memory locations and accessed using indexes. It describes how to declare, initialize, access, and manipulate single and multi-dimensional arrays. It also covers passing arrays to functions, array addressing and calculations, and merging two sorted arrays.

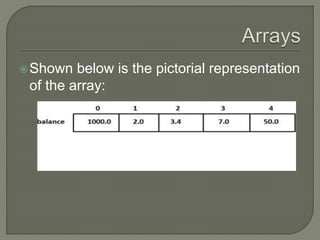
4. Declaration of arrays
type arrayName [ arraySize ];
Ex-double balance[10];

5.  Initializing Arrays
Ex-double balance[5] = {1000.0, 2.0, 3.4, 7.0,
50.0};
If you omit the size of the array, an array just
big enough to hold the initialization is created.
Therefore, if you write −
Ex-double balance[] = {1000.0, 2.0, 3.4, 7.0,
50.0};

6.  Initializing Arrays
Ex-double balance[5] = {1000.0, 2.0, 3.4, 7.0,
50.0};
If you omit the size of the array, an array just
big enough to hold the initialization is created.
Therefore, if you write −
Ex-double balance[] = {1000.0, 2.0, 3.4, 7.0,
50.0};

7. Initializing Arrays
You will create exactly the same array as
you did in the previous example. Following
is an example to assign a single element
of the array −
Ex-balance[4] = 50.0;

8. Shown below is the pictorial representation
of the array:

9. double salary = balance[4];

10. #include <stdio.h>
int main ()
{
int a[10],i,size;
printf(“nhow many no of elements u want to scan”);
scanf(“%d”,&size);
printf(“nEnter the elements in the array”);
for(i=0;i<size;i++)
{
scanf(“%d”,&a[i]);
} //end for
for(i=0;i<size;i++)
{
printf(“The array is %d”,a[i]); //Displaying Array
} //end for
return 0;
}

11. 1
2
3
4
5

12. type name[size1][size2]...[sizeN];

13. multidimensional array is the two-dimensional
array
type arrayName [ x ][ y ];

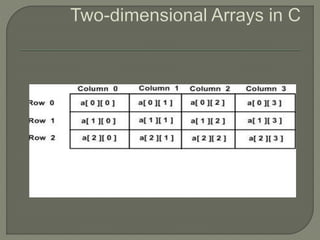
15. Initializing Two-Dimensional Arrays
int a[3][4] = { {0, 1, 2, 3} , /* initializers for
{4, 5, 6, 7} ,
{8, 9, 10, 11} /* initializers for row
/* initializers for row indexed by 2 */ };

16. Accessing Two-Dimensional Array
Elements
int val = a[2][3];

17. For example, the following declaration
creates a three dimensional integer array −
Ex-int threedim[5][10][4];

18. void myFunction(int param[10])
{ . . .
//Statement Excution
}
Passing Arrays as Function
Arguments in C

19. ADT is useful tool for specifying the logical
properties of a data type.
A data type is a collection of values & the
set of operations on the values.
ADT refers to the mathematical concept
that defines the data type.
ADT is not concerned with implementation
but is useful in making use of data type.
Abstract Data Type

20. Arrays are stored in consecutive set of
memory locations.
Array can be thought of as set of index and
values.
For each index which is defined there is a
value associated with that index.
There are two operations permitted on
array data structure .retrieve and store
ADT for an array

21. CREATE()-produces empty array.
RETRIVE(array,index)->value
Takes as input array and index and either
returns appropriate value or an error.
STORE(array,index,value)-array used to
enter new index value pairs.
ADT for an array

22. Representation and analysis
Type variable_name[size]
Operations with arrays:
Copy
Delete
Insert
Search
Sort
Merging of sorting arrays.
Introduction to arrays

23.  #include <stdio.h>

 int main()
 {
 int a[100],b[100] position, c n;

 printf("Enter number of elements in arrayn");
 scanf("%d", &n);

 printf("Enter %d elementsn", n);

 for ( c = 0 ; c < n ; c++ )
 scanf("%d", &a[c]);
 printf("Enter %d elementsn", n);

 for( c = 0 ; c < n - 1 ; c++ )
 printf("%dn", a[c]);
 //Coping the element of array a to b
 for( c = 0 ; c < n - 1 ; c++ )
 {
 b[c]=a[c];
 }
 }

 return 0;
 }
Copy operation

24. 

 Enter number of elements in array -4

 Enter 4 elements

1
 2
 3
 4
 displaying array a
 1
 2
 3
 4
 displaying array b
 1
 2
 3
 4


25.  #include <stdio.h>

 int main()
 {
 int array[100], position, i, n;

 printf("Enter number of elements in arrayn");
 scanf("%d", &n);

 printf("Enter %d elementsn", n);

 for ( i = 0 ; i < n ; i++ )
 scanf("%d", &array[i]);

 printf("Enter the location where you wish to delete elementn");
 scanf("%d", &position);

 for ( i = position ; i < n; i++ )
• {
 array[i] = array[i+1];
 }
 printf("Resultant array isn");

 for( i = 0 ; i < n-1 ; i++ )
 printf("%dn", array[i]);


 return 0;
 }
Delete operation

26. Delete operation

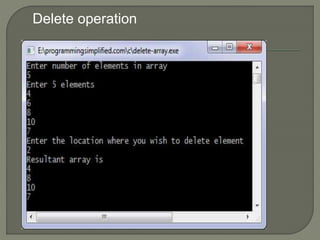
27. #include <stdio.h>
int main()
{
int array[100], position, i, n, value;
printf("Enter number of elements in arrayn");
scanf("%d", &n);
printf("Enter %d elementsn", n);
for (i= 0;i< n; i++)
scanf("%d", &array[i]);
printf("Enter the location where you wish to insert an elementn");
scanf("%d", &position);
printf("Enter the value to insertn");
scanf("%d", &value);
for (i = n - 1; i >= position ; i--)
array[i+1] = array[i];
array[position] = value;
printf("Resultant array isn");
for (i= 0; i <= n; i++)
printf("%dn", array[i]);
return 0;
}
Inserting an element

28. Inserting an element

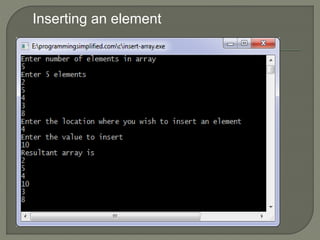
29. Int a[10]={5,4,3,2,1}
for(i=0;i<n-1;i++)
{
for(j=0;j<=n-1;j++)
{
if(a[j]>a[j+1])
{
temp=a[i];
a[i]=a[j];
a[j]=temp;
}
}
Sort an array

30. Reverse array
#include <stdio.h>
int main() {
int array[100], n, i, temp, end;
scanf("%d", &n);
end = n - 1;
for (i = 0; i < n; i++) {
scanf("%d", &array[i]);
}
for (i= 0; < n/2; i++)
{
t emp = array[i];
array[i] = array[end];
array[end] = temp;
end--;
}
printf("Reversed array elements are:n");
for ( i= 0; i < n; i++) {
printf("%dn", array[i]);
}
return 0;
}

31. Sort element using array
int a[10]={5,4,3,2,1}
for(i=0;i<n;i++)
for(j=i+1;j<n;j++)
{
if(a[i]>a[j])
{
temp=a[i];
a[i]=a[j];
a[j]=temp;
}
}

32. Merging of two arrays

33. multidimensional array is the two-dimensional
array
type arrayName [ x ][ y ];

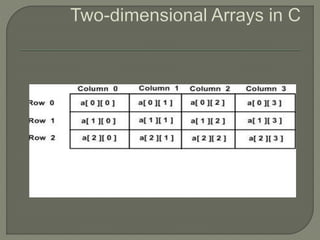
35.  m-no of rows
 n-no of columns
 Printf(“n Enter the rows and columns”);
 Scanf(%d %d”,&m,&n);
 for(i=0;i<m;i++)
 {
• for(j=0;j<n;j++)
• {
 Printf(“n Enter the value of(%d)(%d)=“,i,j);
 Scanf(“%d”,&a[i][j]);
• }

36.  For(i=0;i<m;i++)
 {
• Printf(“n”);
• For(j=0;j<n;j++)
• {

 printf(“%d”,&a[i][j]);
• }
}

37.  int main ()
 { /* an array with 5 rows and 2 columns*/
 int a[5][2] = { {0,0}, {1,2}, {2,4}, {3,6},{4,8}};
 int i, j;
 /* output each array element's value */
 for ( i = 0; i < 5; i++ )
 {
 for ( j = 0; j < 2; j++ )
 {
 printf("a[%d][%d] = %dn", i,j, a[i][j] );
 }
 }
 return 0;
 }

38. Address Calculation in single (one)
Dimension Array:

40.  Array of an element of an array say “A[ I ]” is
calculated using the following formula:
 Address of A [ I ] = B + W * ( I – LB )
 Where,
B = Base address
W = Storage Size of one element stored in the
array (in byte)
I = Subscript of element whose address is to be
found
LB = Lower limit / Lower Bound of subscript, if not
specified assume 0 (zero)

41.  Ex-Given the base address of an
array B[1300…..1900] as 1020 and size of each
element is 2 bytes in the memory. Find the address
of B[1700].
Solution:
 The given values are: B = 1020, LB = 1300, W = 2, I
= 1700
 Address of A [ I ] = B + W * ( I – LB )
 = 1020 + 2 * (1700 – 1300)
= 1020 + 2 * 400
= 1020 + 800
= 1820 [Ans]

42. While storing the elements of a 2-D array in
memory, these are allocated contiguous
memory locations. Therefore, a 2-D array must
be liberalized so as to enable their storage.
There are two alternatives to achieve
linearization: Row-Major and Column-Major.

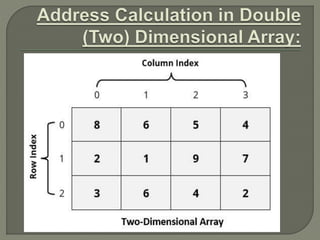
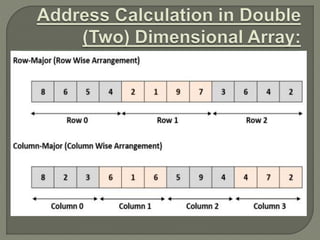
45. Address of an element of any array say “A[ I ][ J
]” is calculated in two forms as given:
(1) Row Major System (2) Column Major System

46. The address of a location in Row Major System is calculated using the
following formula:
Address of A [ I ][ J ] = B + W * [ N * ( I – Lr ) + ( J – Lc )

47. The address of a location in Row Major System is calculated using the
following formula:
Address of A [ I ][ J ] = B + W * [ N * ( I – Lr ) + ( J – Lc )
B = Base address
I = Row subscript of element whose address is to be found
J = Column subscript of element whose address is to be found
W = Storage Size of one element stored in the array (in byte)
Lr = Lower limit of row/start row index of matrix, if not given
assume 0 (zero)
Lc = Lower limit of column/start column index of matrix, if not
given assume 0 (zero)
M = Number of row of the given matrix
N = Number of column of the given matrix

48. Address of A [ I ][ J ] Column Major Wise = B + W * [( I – Lr ) + M * ( J
– Lc )]
Column Major System:
The address of a location in Column Major System is calculated using
the following formula:
B = Base address
I = Row subscript of element whose address is to be found
J = Column subscript of element whose address is to be found
W = Storage Size of one element stored in the array (in byte)
Lr = Lower limit of row/start row index of matrix, if not given
assume 0 (zero)
Lc = Lower limit of column/start column index of matrix, if not
given assume 0 (zero)
M = Number of row of the given matrix
N = Number of column of the given matrix

49. Important : Usually number of rows and columns of a matrix are
given ( like A[20][30] or A[40][60] ) but if it is given as A[Lr- – – –
– Ur, Lc- – – – – Uc]. In this case number of rows and columns
are calculated using the following methods:
Number of rows (M) will be calculated as = (Ur – Lr) + 1
Number of columns (N) will be calculated as = (Uc – Lc) + 1
And rest of the process will remain same as per requirement
(Row Major Wise or Column Major Wise).

50. Examples:
Q 1. An array X [-15……….10, 15……………40] requires one
byte of storage. If beginning location is 1500 determine the
location of X [15][20].
Solution:
As you see here the number of rows and columns are not given in
the question. So they are calculated as:
Number or rows say M = (Ur – Lr) + 1 = [10 – (- 15)] +1 = 26
Number or columns say N = (Uc – Lc) + 1 = [40 – 15)] +1 = 26

51. (i) Column Major Wise Calculation of above equation
The given values are: B = 1500, W = 1 byte, I = 15, J =
20, Lr = -15, Lc = 15, M = 26
Address of A [ I ][ J ]
=B + W * [ ( I – Lr ) + M * ( J – Lc ) ]
= 1500 + 1 * [(15 – (-15)) + 26 * (20 – 15)] = 1500 + 1 *
[30 + 26 * 5] = 1500 + 1 * [160] = 1660 [Ans]

52. = 1500 + 1* [26 * (15 – (-15))) + (20 – 15)]
= 1500 + 1 * [26 * 30 + 5]
= 1500 + 1 * [780 + 5]
= 1500 + 785
= 2285 [Ans]
(ii) Row Major Wise Calculation of above equation
The given values are: B = 1500, W = 1 byte, I = 15, J =
20, Lr = -15, Lc = 15, N = 26
Address of A [ I ][ J ] = B + W * [ N * ( I – Lr ) + ( J – Lc ) ]

53. Merging of two arrays
 int main()
 {
 int arr1[30], arr2[30], res[60];
 int i, j, k, n1, n2;

 printf("nEnter no of elements in 1st array :");
 scanf("%d", &n1);
 for (i = 0; i < n1; i++)
 {
 scanf("%d", &arr1[i]);
 }

 printf("nEnter no of elements in 2nd array :");
 scanf("%d", &n2);
 for (i = 0; i < n2; i++)
 {
 scanf("%d", &arr2[i]);
 }

 i = 0;
 j = 0;
 k = 0;


54. Merging of two arrays
 // Merging starts
 while (i < n1 && j < n2)
 {
 if (arr1[i] <= arr2[j])
 {
 res[k] = arr1[i];
 i++;
 k++;
 }
 else
 {
res[k] = arr2[j];
k++;
j++;
 }
 }


55. Merging of two arrays
/* Some elements in array 'arr1' are still remaining
 where as the array 'arr2' is exhausted */

 while (i < n1)
 {
 res[k] = arr1[i];
 i++;
 k++;
 }

56. Merging of two arrays
/* Some elements in array 'arr2' are still remaining
 where as the array 'arr1' is exhausted */

 while (j < n2) {
 res[k] = arr2[j];
 k++;
 j++;
 }

57. Merging of two arrays
//Displaying elements of array 'res'
printf("nMerged array is :");
for (i = 0; i < n1 + n2; i++)
printf("%d ", res[i]);
return (0);
}

58. Merging of two arrays
/* Some elements in array 'arr2' are still remaining
where as the array 'arr2' is exhausted */
while (i < n2)
{
res[k] = arr2[i];
i++;
k++;
}
for(i=0;i<k;i++)
{
printf(“%d”,res[i]);
}

59. Merging of two arrays
Output:
Enter no of elements in 1st array : 4
11 22 33 44
Enter no of elements in 2nd array : 3
10 40 80
Merged array is : 10 11 22 33 40 44 80