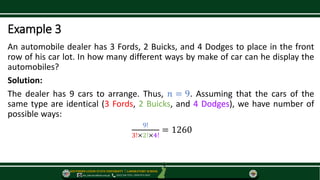
The document outlines the formula for calculating arrangements of identical objects, providing several examples including word permutations and automobile arrangements. It explains specific scenarios involving identical letters in words and conditions where certain letters must appear in order. Additionally, it presents a challenge problem related to arranging boys and girls based on ascent order of height.