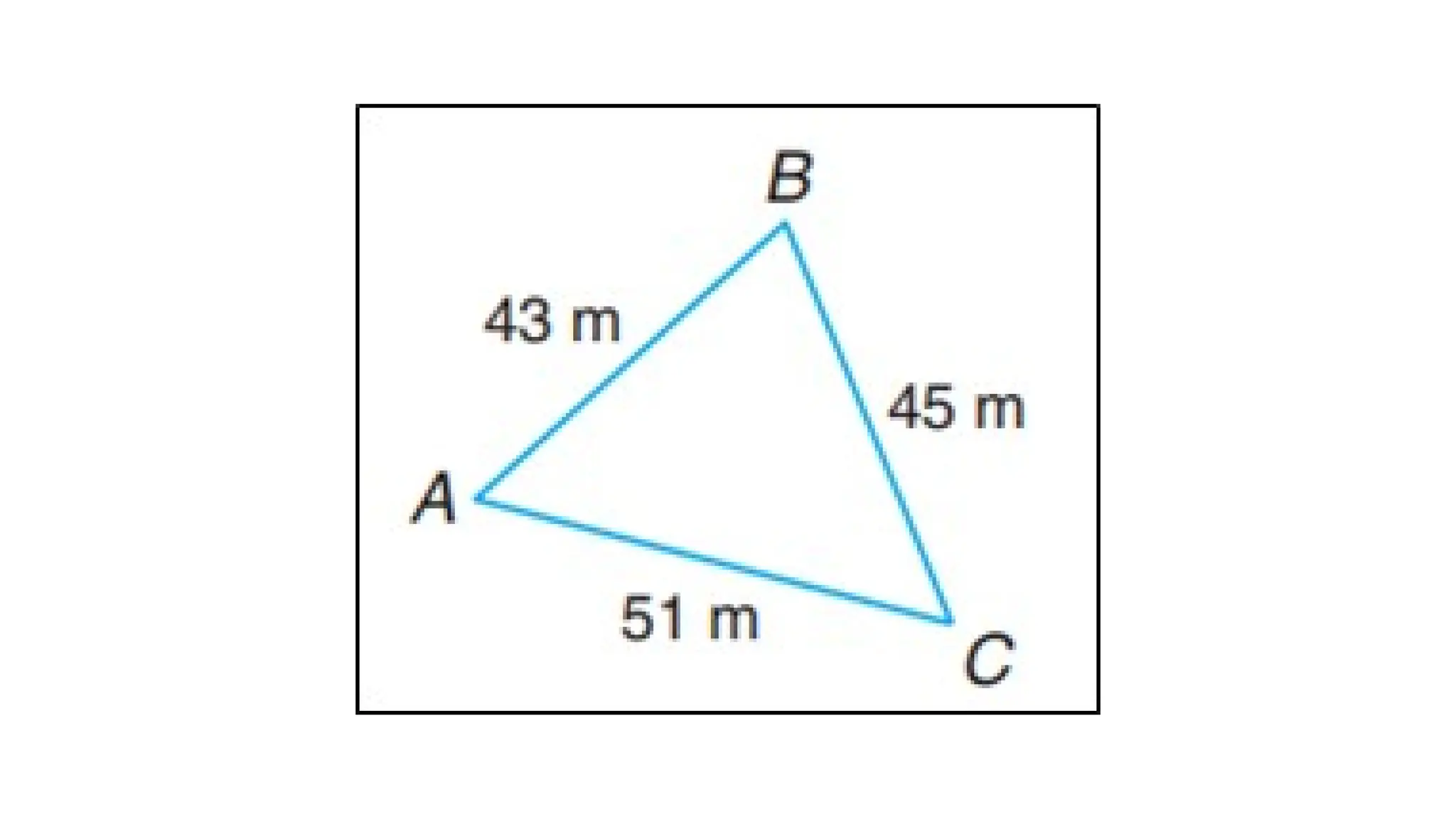
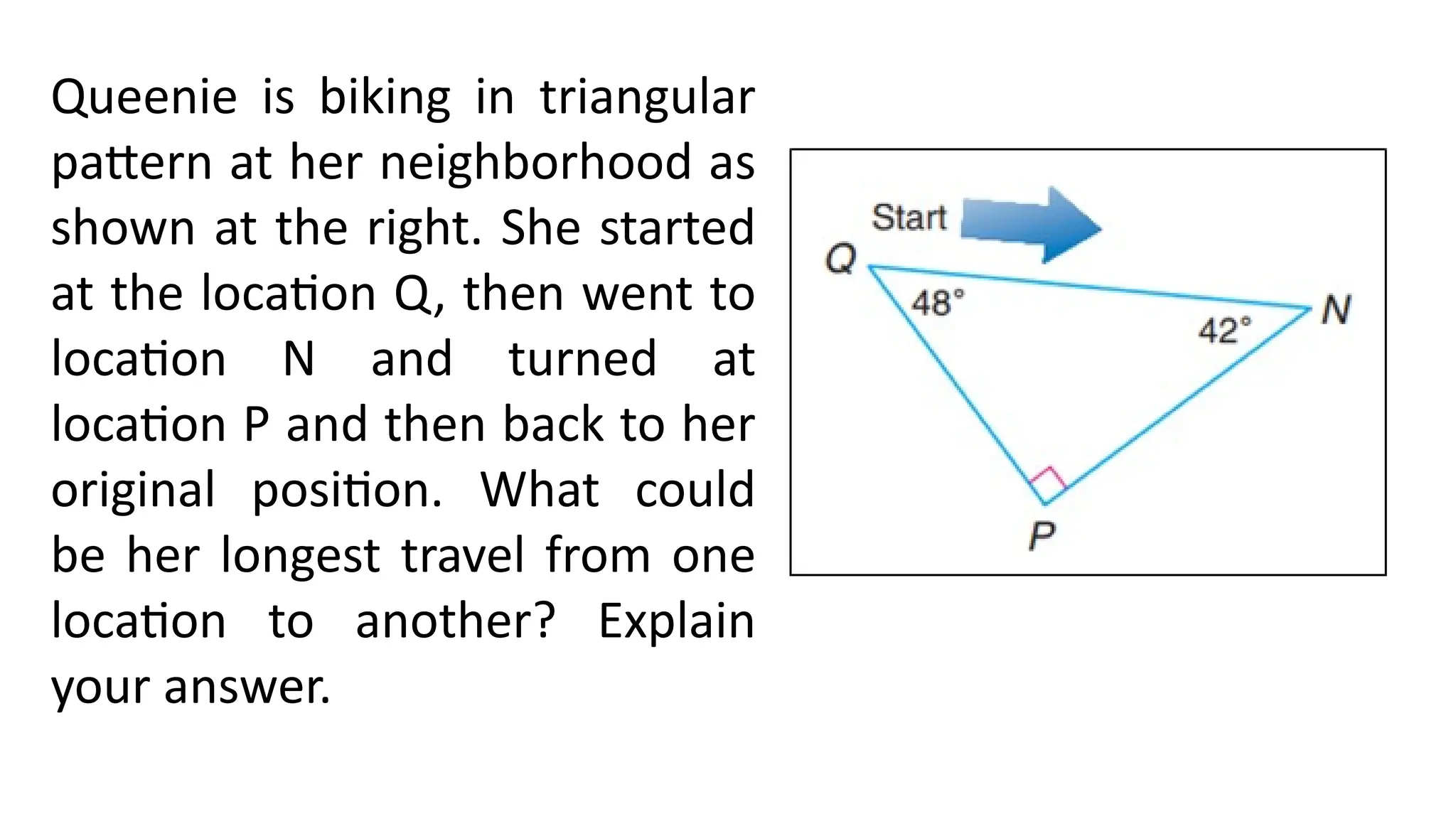
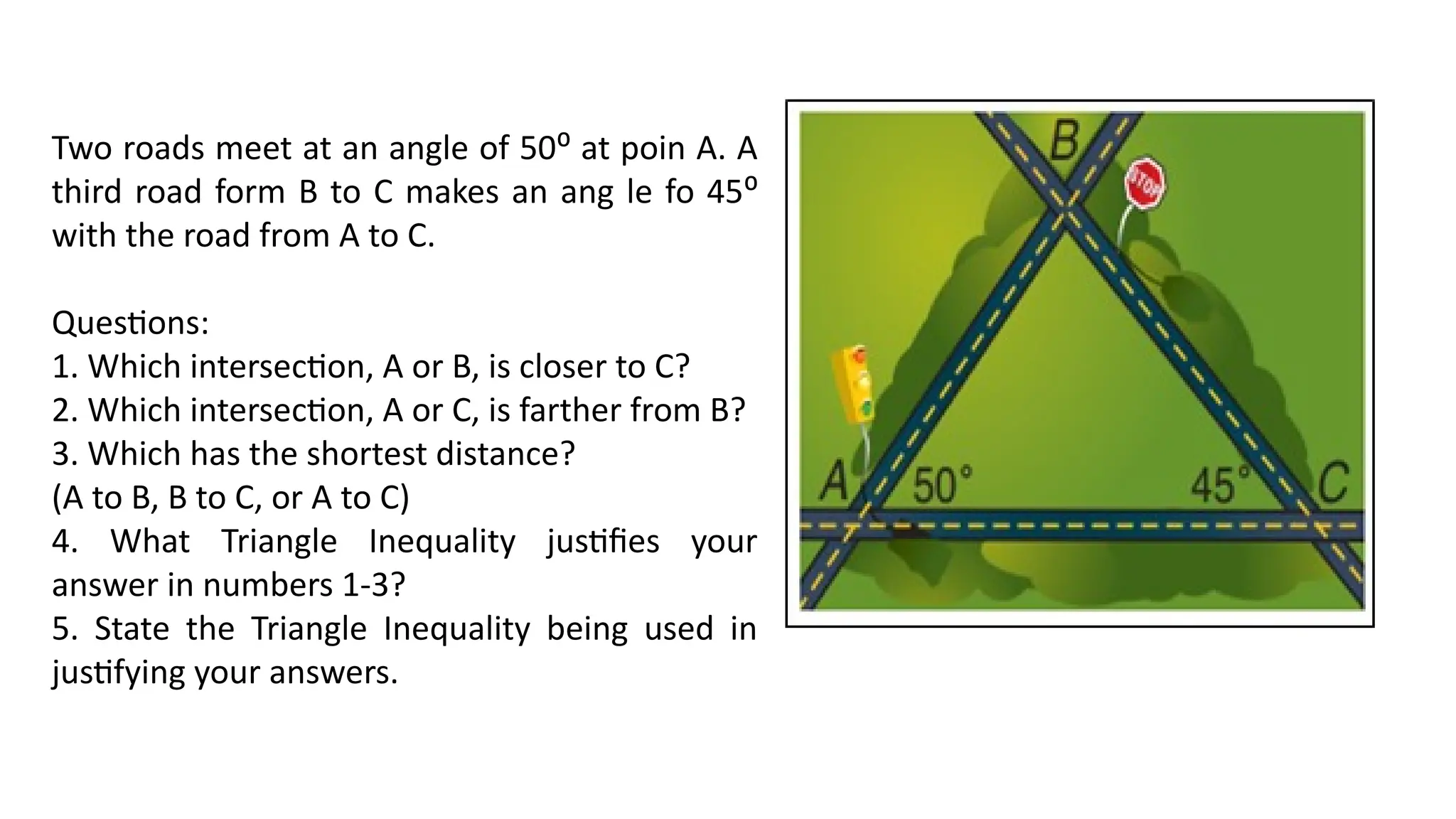
The document discusses various applications of the triangle inequality theorem in different scenarios including biking routes, walking distances, and hiking directions. It poses questions related to distances between points and requires justifications using the theorem. Examples include the comparison of estimated distances and the need to illustrate hiking routes with a map.

1. Application of triangle
inequality theorems

3. 1. 2,3,4
4. 9,5,3
2. 1,2,3
5. 14,7,7
3. 4,4,7

4. Queenie is biking in triangular
pattern at her neighborhood as
shown at the right. She started
at the location Q, then went to
location N and turned at
location P and then back to her
original position. What could
be her longest travel from one
location to another? Explain
your answer.

5. Two roads meet at an angle of 50⁰ at poin A. A
third road form B to C makes an ang le fo 45⁰
with the road from A to C.
Questions:
1. Which intersection, A or B, is closer to C?
2. Which intersection, A or C, is farther from B?
3. Which has the shortest distance?
(A to B, B to C, or A to C)
4. What Triangle Inequality justifies your
answer in numbers 1-3?
5. State the Triangle Inequality being used in
justifying your answers.

6. The distance John Mark walks
from home to school is 120
meters and 80 meters when he
goes to church from home. Eula
estimates that the distance
John Mark walks when he goes
directly to Church, coming from
school, is 180 meters. Rhea’s
estimation is 210 meters.
Which estimation is feasible?
Justify your answer

7. 1. Who between Rhea and Eula got the correct
estimation? Explain.
2. What Triangle Inequality Theorem is being used to
justify the scenario?
3. If you are the one to be asked, what is your
estimation for the distance John Mark walks from the
school to the church?
4. Can you give all the possible distance John Mark
walks from school to church?

8. Little Red Riding Hood went into the forest to visit
her beloved grandma. She walked towards west
from the forest’s entrance for 350 meters. As she
arrived at the biggest pine tree, she went North and
walked another 280 meters. As she walked towards
her grandma’s house, she thought to take the short
cut back home later on the afternoon. How many
meters will Little Red Riding Hood walk when she
will go back home? Write ten possible distance in
meters?

9. Marichu and her friends, went
to a mountain hike at Osmeña
peak. They hiked due North
then turn 60⁰ Northwest after 3
hours of hiking. When they
arrived the peak, they decided
to take another route back to
where they started. They
turned 70⁰ South, hiked, and
went back happily and
contented with their journey.

10. 1. Draw a map illustrating the directions that
Marichu and her friends took. (Use protractor.)
2. Label their starting point T, the location where
they turned O, and the mountain peak P.
3. Arrange the distance of their hike from the
nearest to the farthest