The document provides an overview of advanced predictive modeling techniques using R, including time-series analysis, ARIMA model building, and forecasting methods. It features examples like air passenger data and European retail trade data, showing how to analyze and plot these datasets. Key objectives include understanding predictive modeling concepts, handling real-life datasets, and applying various forecasting techniques.

1. www.edureka.co/advanced-predictive-modelling-in-r
View Advanced Predictive Modelling with R course details at www.edureka.co/advanced-predictive-modelling-in-r
Advanced Predictive Modelling with R
For Queries:
Post on Twitter @edurekaIN: #askEdureka
Post on Facebook /edurekaIN
For more details please contact us:
US : 1800 275 9730 (toll free)
INDIA : +91 88808 62004
Email Us : sales@edureka.co

2. Slide 2 www.edureka.co/advanced-predictive-modelling-in-r
At the end of this module, you will be able to understand:
 Introduction to Predictive Modeling
 Beyond OLS: How real life data-set looks like!
 Decoding Forecasting
 How to handle real life dataset: Two examples
 How to Build Models in R: Example
 Forecasting techniques and Plots
Objectives

3. Slide 3 www.edureka.co/advanced-predictive-modelling-in-r
a <- ts(1:20, frequency = 12, start = c(2011, 3))
print(a)
## Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec
## 2011 1 2 3 4 5 6 7 8 9 10
## 2012 11 12 13 14 15 16 17 18 19 20
str(a)
## Time-Series [1:20] from 2011 to 2013: 1 2 3 4 5 6 7 8 9 10 ...
attributes(a)
## $tsp
## [1] 2011.167 2012.750 12.000
##
## $class
## [1] "ts"
Creating a Simple TimeSeries

4. Slide 4 www.edureka.co/advanced-predictive-modelling-in-r
str(AirPassengers)
## Time-Series [1:144] from 1949 to 1961: 112 118 132 129 121 135 148 148
136 119 ...
summary(AirPassengers)
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 104.0 180.0 265.5 280.3 360.5 622.0
AirPassengers Case

5. Slide 5 www.edureka.co/advanced-predictive-modelling-in-r
apts <- ts(AirPassengers, frequency = 12)
apts
## Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec
## 1 112 118 132 129 121 135 148 148 136 119 104 118
## 2 115 126 141 135 125 149 170 170 158 133 114 140
## 3 145 150 178 163 172 178 199 199 184 162 146 166
## 4 171 180 193 181 183 218 230 242 209 191 172 194
## 5 196 196 236 235 229 243 264 272 237 211 180 201
## 6 204 188 235 227 234 264 302 293 259 229 203 229
## 7 242 233 267 269 270 315 364 347 312 274 237 278
## 8 284 277 317 313 318 374 413 405 355 306 271 306
## 9 315 301 356 348 355 422 465 467 404 347 305 336
## 10 340 318 362 348 363 435 491 505 404 359 310 337
## 11 360 342 406 396 420 472 548 559 463 407 362 405
## 12 417 391 419 461 472 535 622 606 508 461 390 432
Converting it in TS Data

6. Slide 6 www.edureka.co/advanced-predictive-modelling-in-r
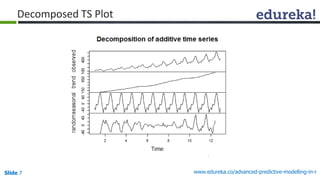
Decomposing the TS
f <- decompose(apts)
> names(f) [1] "x" "seasonal" "trend" "random" "figure" "type"
plot(f$figure, type = "b") # seasonal figures

7. Slide 7 www.edureka.co/advanced-predictive-modelling-in-r
Decomposed TS Plot

8. Slide 8 www.edureka.co/advanced-predictive-modelling-in-r
Building an ARIMA Model
fit <- arima(AirPassengers, order = c(1, 0, 0), list(order = c(2,
1, 0), peri
od = 12))
fit
##
## Call:
## arima(x = AirPassengers, order = c(1, 0, 0), seasonal =
list(order = c(2, 1,
## 0), period = 12))
##
## Coefficients:
## ar1 sar1 sar2
## 0.9458 -0.1333 0.0821
## s.e. 0.0284 0.1035 0.1078
##
## sigma^2 estimated as 143.1: log likelihood = -516.18, aic =
1040.37

9. Slide 9 www.edureka.co/advanced-predictive-modelling-in-r
Forecast
fore <- predict(fit, n.ahead = 24)
fore
## $pred
## Jan Feb Mar Apr May Jun Jul
## 1961 445.0772 418.6286 451.3255 485.0739 496.9859 555.4025 641.1830
## 1962 463.4606 435.4701 463.6918 501.9637 511.8873 571.0617 657.1925
## Aug Sep Oct Nov Dec
## 1961 627.2158 528.6446 478.3612 410.0384 452.4290
## 1962 640.0611 540.7620 491.0499 419.6633 461.3783
##
## $se
## Jan Feb Mar Apr May Jun Jul
## 1961 11.96267 16.46600 19.63824 22.09347 24.07871 25.72521 27.11359
## 1962 35.68346 38.94721 41.65083 43.92872 45.87078 47.54098 48.98693
## Aug Sep Oct Nov Dec
## 1961 28.29798 29.31703 30.19955 30.96776 31.63920
## 1962 50.24524 51.34481 52.30891 53.15659 53.90364

10. Slide 10 www.edureka.co/advanced-predictive-modelling-in-r
Upper and Lower Confidence Interval
fore <- predict(fit, n.ahead = 24)
fore
## $pred
## Jan Feb Mar Apr May Jun Jul
## 1961 445.0772 418.6286 451.3255 485.0739 496.9859 555.4025 641.1830
## 1962 463.4606 435.4701 463.6918 501.9637 511.8873 571.0617 657.1925
## Aug Sep Oct Nov Dec
## 1961 627.2158 528.6446 478.3612 410.0384 452.4290
## 1962 640.0611 540.7620 491.0499 419.6633 461.3783
##
## $se
## Jan Feb Mar Apr May Jun Jul
## 1961 11.96267 16.46600 19.63824 22.09347 24.07871 25.72521 27.11359
## 1962 35.68346 38.94721 41.65083 43.92872 45.87078 47.54098 48.98693
## Aug Sep Oct Nov Dec
## 1961 28.29798 29.31703 30.19955 30.96776 31.63920
## 1962 50.24524 51.34481 52.30891 53.15659 53.90364
# error bounds at 95% confidence level
U <- fore$pred + 2 * fore$se
L <- fore$pred - 2 * fore$se
U
## Jan Feb Mar Apr May Jun Jul
## 1961 469.0025 451.5606 490.6020 529.2609 545.1433 606.8530 695.4102
## 1962 534.8275 513.3645 546.9934 589.8211 603.6288 666.1437 755.1663
## Aug Sep Oct Nov Dec
## 1961 683.8117 587.2786 538.7603 471.9739 515.7074
## 1962 740.5516 643.4516 595.6677 525.9765 569.1856
L
## Jan Feb Mar Apr May Jun Jul
## 1961 421.1519 385.6966 412.0491 440.8870 448.8284 503.9521 586.9558
## 1962 392.0937 357.5757 380.3901 414.1063 420.1457 475.9797 559.2186
## Aug Sep Oct Nov Dec
## 1961 570.6198 470.0105 417.9621 348.1029 389.1506
## 1962 539.5707 438.0724 386.4321 313.3501 353.5710

11. Slide 11 www.edureka.co/advanced-predictive-modelling-in-r
Plot the Forecast
ts.plot(AirPassengers, fore$pred, U, L,
col = c(1, 2, 4, 4), lty = c(1, 1, 2, 2))
legend("topleft", col = c(1, 2, 4), lty = c(1, 1, 2),
c("Actual", "Forecast", "Error Bounds (95% Confidence)"))

12. Slide 12 www.edureka.co/advanced-predictive-modelling-in-r
European Quarterly Retail Trade
• > euretail
• Qtr1 Qtr2 Qtr3 Qtr4
• 1996 89.13 89.52 89.88 90.12
• 1997 89.19 89.78 90.03 90.38
• 1998 90.27 90.77 91.85 92.51
• 1999 92.21 92.52 93.62 94.15
• 2000 94.69 95.34 96.04 96.30
• 2001 94.83 95.14 95.86 95.83
• 2002 95.73 96.36 96.89 97.01
• 2003 96.66 97.76 97.83 97.76
• 2004 98.17 98.55 99.31 99.44
• 2005 99.43 99.84 100.32 100.40
• 2006 99.88 100.19 100.75 101.01
• 2007 100.84 101.34 101.94 102.10
• 2008 101.56 101.48 101.13 100.34
• 2009 98.93 98.31 97.67 97.44
• 2010 96.53 96.56 96.51 96.70
• 2011 95.88 95.84 95.79 95.97

13. Slide 13 www.edureka.co/advanced-predictive-modelling-in-r
European Quarterly Retail Trade (Contd.)
plot(euretail, ylab="Retail index", xlab="Year")

14. Slide 14 www.edureka.co/advanced-predictive-modelling-in-r
Plotting the first Differenced TS
tsdisplay(diff(euretail,4))

15. Slide 15 www.edureka.co/advanced-predictive-modelling-in-r
Difference of Difference
tsdisplay(diff(diff(euretail,4)))
The significant spike at lag 1 in the ACF
suggests a non-seasonal MA(1) component,
and the significant spike at lag 4 in the ACF
suggests a seasonal MA(1) component
Consequently, we begin with an
ARIMA(0,1,1)(0,1,1)4 model,
indicating a first and seasonal difference,
and non-seasonal and seasonal MA(1)
components

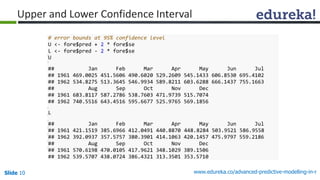
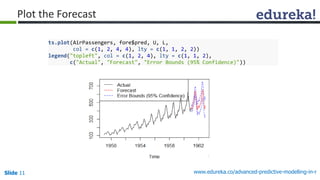
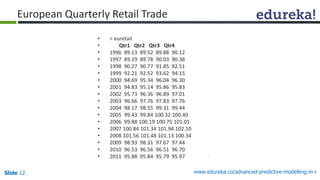
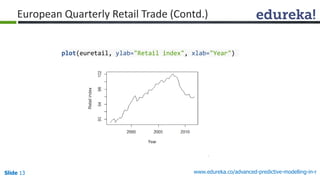
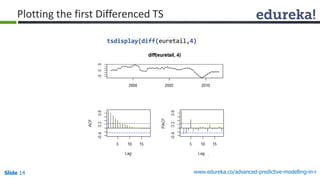
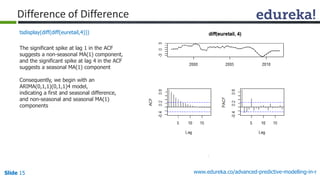
16. Slide 16 www.edureka.co/advanced-predictive-modelling-in-r
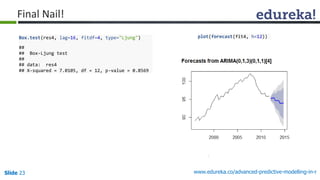
Fitting a Model
fit <- Arima(euretail, order=c(0,1,1), seasonal=c(0,1,1))
fit
## Series: euretail
## ARIMA(0,1,1)(0,1,1)[4]
##
## Coefficients:
## ma1 sma1
## 0.2901 -0.6909
## s.e. 0.1118 0.1197
##
## sigma^2 estimated as 0.1812: log likelihood=-34.68
## AIC=75.36 AICc=75.79 BIC=81.59

17. Slide 17 www.edureka.co/advanced-predictive-modelling-in-r
Plotting the Residual
tsdisplay(residuals(fit))

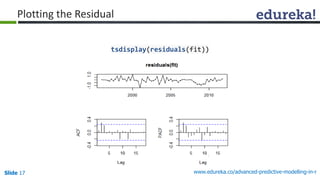
18. Slide 18 www.edureka.co/advanced-predictive-modelling-in-r
Lets Tweak the Model
### Lets tweak the Model and try
fit3 <- Arima(euretail, order=c(0,1,3), seasonal=c(0,1,1))
fit3
## Series: euretail
## ARIMA(0,1,3)(0,1,1)[4]
##
## Coefficients:
## ma1 ma2 ma3 sma1
## 0.2625 0.3697 0.4194 -0.6615
## s.e. 0.1239 0.1260 0.1296 0.1555
##
## sigma^2 estimated as 0.1451: log likelihood=-28.7
## AIC=67.4 AICc=68.53 BIC=77.78

19. Slide 19 www.edureka.co/advanced-predictive-modelling-in-r
Plotting the Residual, Again!
res <- residuals(fit3)
tsdisplay(res)
Box.test(res, lag=16, fitdf=4, type="Ljung")
##
## Box-Ljung test
##
## data: res
## X-squared = 7.0105, df = 12, p-value = 0.8569

20. Slide 20 www.edureka.co/advanced-predictive-modelling-in-r
Forecast and Plot
plot(forecast(fit3, h=12))

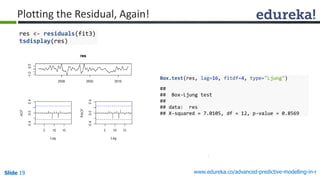
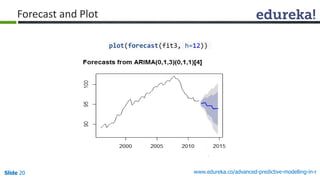
21. Slide 21 www.edureka.co/advanced-predictive-modelling-in-r
Can R Do It Automatically For Us??
auto.arima(euretail)
## Series: euretail
## ARIMA(1,1,1)(0,1,1)[4]
##
## Coefficients:
## ar1 ma1 sma1
## 0.8828 -0.5208 -0.9704
## s.e. 0.1424 0.1755 0.6792
##
## sigma^2 estimated as 0.1411: log likelihood=-30.19
## AIC=68.37 AICc=69.11 BIC=76.68
auto.arima(euretail, stepwise=FALSE, approximation=FALSE)
## Series: euretail
## ARIMA(0,1,3)(0,1,1)[4]
##
## Coefficients:
## ma1 ma2 ma3 sma1
## 0.2625 0.3697 0.4194 -0.6615
## s.e. 0.1239 0.1260 0.1296 0.1555
##
## sigma^2 estimated as 0.1451: log likelihood=-28.7
## AIC=67.4 AICc=68.53 BIC=77.78

22. Slide 22 www.edureka.co/advanced-predictive-modelling-in-r
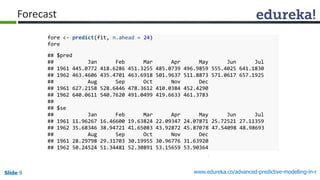
Final Model
fit4<-auto.arima(euretail, stepwise=FALSE, approximation=FALSE)
fit4
## Series: euretail
## ARIMA(0,1,3)(0,1,1)[4]
##
## Coefficients:
## ma1 ma2 ma3 sma1
## 0.2625 0.3697 0.4194 -0.6615
## s.e. 0.1239 0.1260 0.1296 0.1555
##
## sigma^2 estimated as 0.1451: log likelihood=-28.7
## AIC=67.4 AICc=68.53 BIC=77.78
res4 <- residuals(fit4)
tsdisplay(res4)

23. Slide 23 www.edureka.co/advanced-predictive-modelling-in-r
Final Nail!
Box.test(res4, lag=16, fitdf=4, type="Ljung")
##
## Box-Ljung test
##
## data: res4
## X-squared = 7.0105, df = 12, p-value = 0.8569
plot(forecast(fit4, h=12))

24. Slide 24 www.edureka.co/advanced-predictive-modelling-in-r
DIY: Corticosteroid Drug Sales in Australia
 We will try to forecast monthly corticosteroid drug sales in Australia
 These are known as H02 drugs under the Anatomical Therapeutical Chemical classification scheme
fit <- auto.arima(h02, lambda=0, d=0, D=1, max.order=9,stepwise=FALSE, approximation=FALSE)
tsdisplay(residuals(fit))
Box.test(residuals(fit), lag=36, fitdf=8, type="Ljung")
fit <- Arima(h02, order=c(3,0,1), seasonal=c(0,1,2), lambda=0)
plot(forecast(fit), ylab="H02 sales (million scripts)", xlab="Year")

25. Slide 25 www.edureka.co/advanced-predictive-modelling-in-r
 Module 1
» Basic Statistics in R
 Module 2
» Ordinary Least Square Regression 1
 Module 3
» Ordinary Least Square Regression 2
 Module 4
» Ordinary Least Square Regression 3
 Module 5
» Logistic Regression 1
 Module 6
» Logistic Regression 2
 Module 7
» Logistic Regression 3
 Module 8
» Imputation
Course Topics
 Module 9
» Forecasting 1
 Module 10
» Forecasting 2
 Module 11
» Forecasting 3
 Module 12
» Survival Analysis
 Module 13
» Data Mining and Regression
 Module 14
» Big Picture
 Module 15
» Project - Implementation
 Module 16
» Project - Presentation

26. Slide 26 www.edureka.co/advanced-predictive-modelling-in-r
LIVE Online Class
Class Recording in LMS
24/7 Post Class Support
Module Wise Quiz
Project Work
Verifiable Certificate
How it Works

27. Slide 27 www.edureka.co/advanced-predictive-modelling-in-r