The document contains 6 math exercises involving vectors and matrices. In exercise 1, it finds the sum and unit vector of two vectors, and the angle between them. Exercise 2 involves taking the cross product of two vectors. Exercise 3 multiplies matrices and adds the result to another matrix. Exercise 4 finds the inverse of a matrix using Gaussian elimination and the adjugate method. Exercise 5 inverts a matrix using Gaussian elimination. Exercise 6 calculates the determinant of a matrix using cofactor expansion and Sarrus' rule.

1. Ejercicio 1
Ejercicio 2
b. 𝑣
⃗ = (1, 0, −1) y w
⃗⃗⃗⃗ = (1, −4, −2)
𝐿𝑎 𝑠𝑢𝑚𝑎 𝑢
⃗⃗ = 𝑣
⃗ + 𝑤
⃗⃗⃗
𝑢
⃗⃗ = (1 + 1) + (0 − 4) + (−1 − 2)
𝑢
⃗⃗ = (2, −4, −3)
𝐿𝑎 𝑚𝑎𝑔𝑛𝑖𝑡𝑢𝑑 |𝑢
⃗⃗|
|𝑢
⃗⃗| = √(1 + 1)2 + (0 − 4)2 + (−1 − 2)2
|𝑢
⃗⃗| = 5.3851
𝑣𝑒𝑐𝑡𝑜𝑟 𝑢𝑛𝑖𝑡𝑎𝑟𝑖𝑜 𝑢
⃗⃗
𝑢
⃗⃗ =
(3, 4, 6)
5.3851
𝑢
⃗⃗ = (
2
5.3851
,
−4
5.3851
,
−3
5.3851
)

2. 𝑢
⃗⃗ = (0.371, −0.7427, −0.557)
𝐶𝑜𝑠𝑒𝑛𝑜 𝑑𝑒𝑙 𝑎𝑛𝑔𝑢𝑙𝑜 𝑒𝑛𝑡𝑟𝑒 𝑣
⃗ 𝑦 𝑤
⃗⃗⃗
cos 𝛼 =
𝑣
⃗ ∙ 𝑤
⃗⃗⃗
|𝑣
⃗||𝑤
⃗⃗⃗|
cos 𝛼 =
(1 ∙ 1) + (0 ∙ 4) + (−1 ∙ −2)
√12 + 02 + (−1)2 ∙ √12 + (−4)2 + (−2)2
cos𝛼 = 0.4629
𝛼 = cos−1
0.4629
𝛼 = 62,42°
Ejercicio 3
b. 𝑢
⃗⃗ = (−1, 7, −2) y v
⃗⃗ = (6, −2, −1)
𝑃𝑟𝑜𝑑𝑢𝑐𝑡𝑜 𝑐𝑟𝑢𝑧 𝑢
⃗⃗ × 𝑣
⃗
𝑢
⃗⃗ × 𝑣
⃗ = [
𝑖 𝑗 𝑘
−1 7 −2
6 −2 −1
]
𝑢
⃗⃗ × 𝑣
⃗ = ((7 ∙ −1) − (−2 ∙ −2))𝑖 − ((−1 ∙ −1) − (6 ∙ −2))𝑗 + ((−1 ∙ −2) − (6 ∙ 7))𝑘
𝑢
⃗⃗ × 𝑣
⃗ = (−7 − 4)𝑖 − (1 + 12)𝑗 + (2 − 42)𝑘
𝑢
⃗⃗ × 𝑣
⃗ = −11𝑖 − 13𝑗 − 40𝑘

3. Ejercicio 4
b. u = (5B) ∙ C + 𝐴𝑇
5𝐵 = [
5 × 4 5 × −2
5 × 3 5 × 5
5 × 1 5 × −4
] = [
20 −10
15 25
5 −20
]
(5𝐵) ∙ 𝐶 = [
20 −10
15 25
5 −20
] ∙ [
2 7 3
1 −2 0
]
(5𝐵) ∙ 𝐶 = [
(20 × 2) + (−10 × 1) (20 × 7) + (−10 × −2) (20 × 3) + (−10 × 0)
(15 × 2) + (25 × 1) (15 × 7) + (25 × −2) (15 × 3) + (25 × 0)
(5 × 2) + (−20 × 1) (5 × 7) + (−20 × −2) (5 × 3) + (−20 × 0)
]
(5𝐵) ∙ 𝐶 = [
40 − 10 140 + 20 60 + 0
30 + 25 105 − 50 45 + 0
10 − 20 35 + 40 15 + 0
]
(5𝐵) ∙ 𝐶 = [
30 160 60
55 55 45
−10 75 15
]
𝐴𝑇
= [
5 3 −1
−3 −1 1
−3 0 2
]

4. u = (5B) ∙ C + 𝐴𝑇
= [
30 160 60
55 55 45
−10 75 15
] + [
5 3 −1
−3 −1 1
−3 0 2
]
u = (5B) ∙ C + 𝐴𝑇
= [
30 + 5 160 + 3 60 − 1
55 − 3 55 − 1 45 + 1
−10 − 3 75 + 0 15 + 2
]
u = (5B) ∙ C + 𝐴𝑇
= [
35 163 59
52 54 46
−13 75 17
]
Ejercicio 5
b. 𝐵 = [
1 −2 1
1 3 1
2 1 0
]
Método de Gauss
[
1 −2 1
1 3 1
2 1 0
|
1 0 0
0 1 0
0 0 1
]
[
1 −2 1
1 3 1
2 1 0
|
1 0 0
0 1 0
0 0 1
] 𝐹2 = 𝐹2 − 𝐹1
𝐹3 = 𝐹3 − 2𝐹1
[
1 −2 1
0 5 0
0 5 −2
|
1 0 0
−1 1 0
−2 0 1
] 𝐹2 = 𝐹2/5
𝐹3 = 𝐹3 − 5𝐹2

5. [
1 −2 1
0 1 0
0 0 −2
|
1 0 0
−1/5 1/5 0
−1 −1 1
]
𝐹1 = 𝐹1 + 2𝐹2
𝐹3 = 𝐹3/−2
[
1 0 1
0 1 0
0 0 1
|
3/5 2/5 0
−1/5 1/5 0
1/2 1/2 −1/2
]
𝐹1 = 𝐹1 − 𝐹3
[
1 0 0
0 1 0
0 0 1
|
1/10 −1/10 1/2
−1/5 1/5 0
1/2 1/2 −1/2
]
𝐵−1
= [
1/10 −1/10 1/2
−1/5 1/5 0
1/2 1/2 −1/2
]
Método matriz adjunta y el determinante
det (𝐵) =
[
1 −2 1
1 3 1
2
1
1
1
−2
3
0
1
1]
det (𝐵) = (0 + 1 − 4) − (0 + 1 + 6)
det (𝐵) = −3 − 7
det (𝐵) = −10
𝐵𝑇
= [
1 1 2
−2 3 1
1 1 0
]
𝑎𝑑𝑗(𝐵𝑇
) =
[
[
3 1
1 0
] − [
−2 1
1 0
] [
−2 3
1 1
]
− [
1 2
1 0
] [
1 2
1 0
] − [
1 1
1 1
]
[
1 2
3 1
] − [
1 2
−2 1
] [
1 1
−2 3
]]
𝑎𝑑𝑗(𝐵𝑇
) = [
−1 −(−1) −2 − 3
−(−2) −2 0
1 − 6 −(1 + 4) 3 + 2
]

6. 𝑎𝑑𝑗(𝐵𝑇
) = [
−1 1 −5
2 −2 0
−5 −5 5
]
𝐵−1
=
𝑎𝑑𝑗(𝐵𝑇
)
det (𝐵)
= [
−1/−10 1/−10 −5/−10
2/−10 −2/−10 0/−10
−5/−10 −5/−10 5/−10
]
𝐵−1
=
𝑎𝑑𝑗(𝐵𝑇
)
det (𝐵)
= [
1/10 −1/10 1/2
−1/5 1/5 0
1/2 1/2 −1/2
]
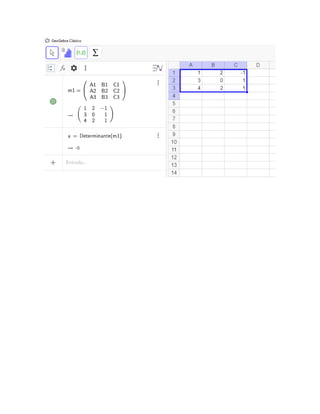
Ejercicio 6
Método de cofactores primera fila
A = [
1 2 −1
3 0 1
4 2 1
]
det(A) = 1 [
0 1
2 1
] − 2 [
3 1
4 1
] + (−1) [
3 0
4 2
]
det(A) = 1(0 − 2) − 2(3 − 4) + (−1)(6 − 0)
det(A) = −2 + 2 − 6
det(A) = −6
Método de cofactores segunda fila
A = [
1 2 −1
3 0 1
4 2 1
]

7. det(A) = −(3) [
2 −1
2 1
] + 0 [
1 −1
4 1
] − (1) [
1 2
4 2
]
det(A) = −3(2 − (−2)) + 0(1 − (−4)) − (1)(2 − 8)
det(A) = −12 + 0 + 6
det(A) = −6
Método de cofactores tercera fila
A = [
1 2 −1
3 0 1
4 2 1
]
det(A) = 4 [
2 −1
0 1
] − 2 [
1 −1
3 1
] + (1) [
1 2
3 0
]
det(A) = 4(2 − 0) − 2(1 − (−3)) + (1)(0 − 6)
det(A) = 8 − 8 − 6
det(A) = −6
Método de Sarrus
A = [
1 2 −1
3 0 1
4 2 1
]
det (𝐴) =
[
1 2 −1
3 0 1
4
1
3
2
2
0
1
−1
1 ]
det (𝐴) =
[
1 2 −1
3 0 1
4
1
3
2
2
0
1
−1
1 ]
det (𝐴) = (0 − 6 + 8) − (0 + 2 + 6)
det (𝐴) = 2 − 8
det (𝐴) = −6
Por cualquier método el determinante da igual. Sin embargo, me parece más sencillo el método de
cofactores en la primera fila.