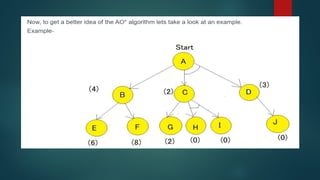
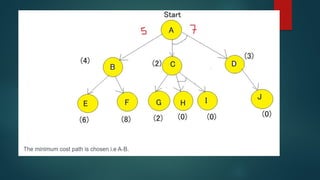
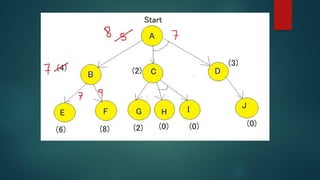
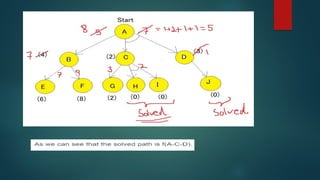
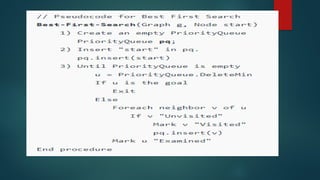
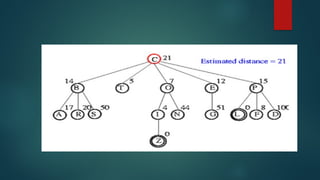
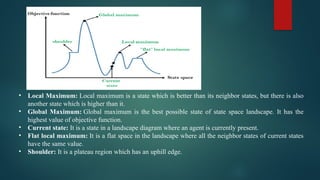
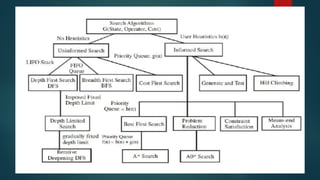
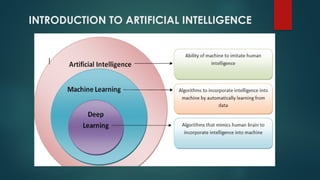
The document is an extensive overview of artificial intelligence (AI), covering its definitions, goals, techniques, and applications, including machine learning, deep learning, and natural language processing. It discusses the advantages and disadvantages of AI, evaluation criteria for AI systems, and various problem-solving approaches such as state space search and production systems. Additionally, it highlights issues in designing search programs and elucidates search algorithms like breadth-first search, depth-first search, and A* algorithm.






























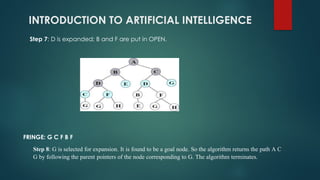











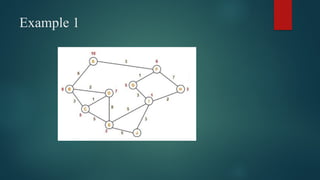
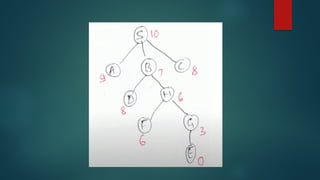
![Example: 2
Path found: ['A', 'E', 'D', 'G']](https://image.slidesharecdn.com/aiunit-1ppt-241029123448-7ffa8cd6/85/AI-Unit-1-PPT-pptx-https-https-plans-to-go-49-320.jpg)