Recommended
PPTX
PPTX
PPT
PPTX
[14.12.08] 행렬대수(ShaderStudy)
PPS
DOC
Govan irma paper 2008 (2) ed
PDF
Sillabario_minimo_necessario_3
PPT
Technology in english classes
PDF
2024 Trend Updates: What Really Works In SEO & Content Marketing
PDF
Storytelling For The Web: Integrate Storytelling in your Design Process
PDF
Artificial Intelligence, Data and Competition – SCHREPEL – June 2024 OECD dis...
PDF
How to Leverage AI to Boost Employee Wellness - Lydia Di Francesco - SocialHR...
PDF
2024 State of Marketing Report – by Hubspot
PDF
Everything You Need To Know About ChatGPT
PDF
Product Design Trends in 2024 | Teenage Engineerings
PDF
How Race, Age and Gender Shape Attitudes Towards Mental Health
PDF
AI Trends in Creative Operations 2024 by Artwork Flow.pdf
PDF
PDF
PEPSICO Presentation to CAGNY Conference Feb 2024
PDF
Content Methodology: A Best Practices Report (Webinar)
PPTX
How to Prepare For a Successful Job Search for 2024
PDF
Social Media Marketing Trends 2024 // The Global Indie Insights
PDF
Trends In Paid Search: Navigating The Digital Landscape In 2024
PDF
5 Public speaking tips from TED - Visualized summary
PDF
ChatGPT and the Future of Work - Clark Boyd
PDF
Getting into the tech field. what next
PDF
Google's Just Not That Into You: Understanding Core Updates & Search Intent
PDF
How to have difficult conversations
More Related Content
PPTX
PPTX
PPT
PPTX
[14.12.08] 행렬대수(ShaderStudy)
PPS
DOC
Govan irma paper 2008 (2) ed
PDF
Sillabario_minimo_necessario_3
PPT
Technology in english classes
Featured
PDF
2024 Trend Updates: What Really Works In SEO & Content Marketing
PDF
Storytelling For The Web: Integrate Storytelling in your Design Process
PDF
Artificial Intelligence, Data and Competition – SCHREPEL – June 2024 OECD dis...
PDF
How to Leverage AI to Boost Employee Wellness - Lydia Di Francesco - SocialHR...
PDF
2024 State of Marketing Report – by Hubspot
PDF
Everything You Need To Know About ChatGPT
PDF
Product Design Trends in 2024 | Teenage Engineerings
PDF
How Race, Age and Gender Shape Attitudes Towards Mental Health
PDF
AI Trends in Creative Operations 2024 by Artwork Flow.pdf
PDF
PDF
PEPSICO Presentation to CAGNY Conference Feb 2024
PDF
Content Methodology: A Best Practices Report (Webinar)
PPTX
How to Prepare For a Successful Job Search for 2024
PDF
Social Media Marketing Trends 2024 // The Global Indie Insights
PDF
Trends In Paid Search: Navigating The Digital Landscape In 2024
PDF
5 Public speaking tips from TED - Visualized summary
PDF
ChatGPT and the Future of Work - Clark Boyd
PDF
Getting into the tech field. what next
PDF
Google's Just Not That Into You: Understanding Core Updates & Search Intent
PDF
How to have difficult conversations
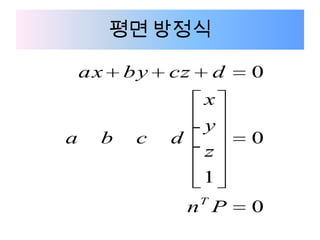
Affine transformations 3 1. 2. 평면 방정식
ax by cz d 0
x
y
a b c d 0
z
1
T
n P 0
3. n ( MP) 0 <= P를 M에 의해 변환
T
n' Qn <= 미지의 변환행렬 Q
T T T T
n ( MP) (Qn) ( MP) n Q MP 0
T
Q M I
1 T
Q (M )
1 T
n' ( M ) n
4. M-1이 존재하지 않을 경우? 행렬식의 분모가 0
1 1 adj
M M
det(M )
T T 1
n P (n M )P 0
T 1
det (M ) (n M )P det (M ) 0
T 1 adj
n det (M ) M P 0
det (M )
T adj
n M P 0
5. 행렬 분해
• Scene Graph(물체 계층)를 통한 Affine행렬을
결합
W A body A arm
Tbody R body Sbody TarmR armSarm
• 합쳐진 행렬 W를 기본Affine 행렬로 분해
W=TRS
• 위의 형식으로 분해가 어려운 경우가 많다.
여러가지 어려운 공식들….
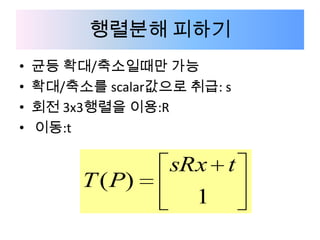
6. 행렬분해 피하기
• 균등 확대/축소일때만 가능
• 확대/축소를 scalar값으로 취급: s
• 회전 3x3행렬을 이용:R
• 이동:t
sRx t
T ( P)
1
7. M M 1M 0 T1 R1S1T0 R0 S 0
I t1 R1 0 s1 I 0 I t0 R0 0 s0 I 0
T T T T T T
0 1 0 1 0 1 0 1 0 1 0 1
s1 R1 t1 s0 R0 t0
0T 1 0T 1
s1s0 R1 R0 s1 R1t0 t1
0T 1
s s1s0
R R1 R0
t s1 R1t0 t1