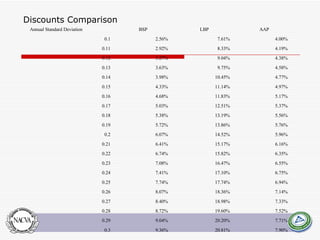
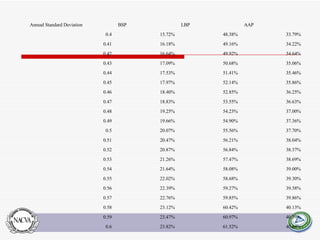
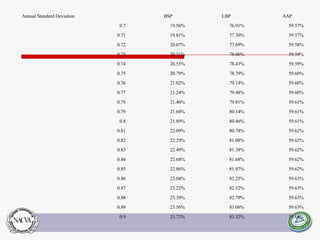
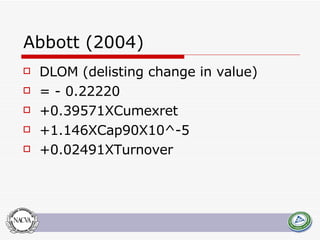
This document summarizes and compares several quantitative models for estimating discounts for lack of marketability (DLOM) and liquidity. It defines key concepts like marketability, liquidity, and degrees of marketability. It then describes several DLOM models including the QMDM, Silber, Bajaj, Abbott, Tabak, Meulbroek, and option-based models like Black-Scholes put, average price Asian put, and lookback put. The document estimates potential DLOM discounts under different volatility and time assumptions using these models for comparative analysis.

1. “ Valuation and Financial Forensics – Educate, Communicate, Preserve” NACVA and IBA’s Annual Consultants’ Conference Discount for Lack of Marketability (Liquidity) Models: A Comparative Analysis Mainstream Track and Ashok Abbott, PhD present May 27-30, 2009 Boston, MA

2. Please set pagers, cell phones, etc. on vibrate mode or turn them off. Please complete and hand in the Presenter Evaluation forms. Don’t forget to complete your CPE Attestation Form. Add your NACVA# (located on your name badge) and sign it. Keep the white copy for your records. Turn in the yellow copy at the NACVA Registration Desk.

3. Discount for Lack of Marketability (Liquidity) Models: A Comparative Analysis Ashok Abbott, PhD

4. Comparative Analysis of Liquidity and Marketability Discount Models

5. Core Concepts in Discounting Marketability Liquidity Holding period Liquidation period Price pressure Price risk/volatility

6. Distinction between Marketability and Liquidity Marketability and Liquidity are aligned but distinct concepts. Marketability -The capability and ease of transfer or salability of an asset, business, business ownership interest or security. Liquidity-The ability to readily convert an asset, business, business ownership interest or security into cash without significant loss of principal.

7. Marketability versus liquidity: ASA definitions adopted July 2004 Marketability: The capability and ease of transfer or salability of an asset, business, business ownership interest or security Liquidity: The ability to readily convert an asset, business, business ownership interest or security into cash without significant loss of principal

8. Degrees of Marketability Registered stock in an Exchange Listed Publicly Traded firm Registered stock in an Exchange Listed Publicly Traded firm subject to Reg 144 restrictions Unregistered stock in an Exchange Listed Publicly Traded firm Unregistered stock in a closely held unlisted large firm (potential to go public) Unregistered stock in a closely held unlisted small firm

9. Model Classes for DLOM QMDM- Quantitative Model of Discount for Marketability, proposed by Z. Christopher Mercer(1997) Time Value Model proposed by John J.Stockdale (2006) CAPM based approach to calculating illiquidity discounts proposed by David I. Tabak which deals with lack of diversification Meulbroek model for cost of lack of diversification Proposed by Lisa K. Meulbroek(2002) Time Volatility Models

10. Models considering Marketability and assuming Liquidity Restricted Stock Discounts Registered vs. Unregistered Stock IPO cost studies

11. Silber Model LN (RPRS) = 4.33 + 0.036 LN (REV) - 0.142 LN (RBRT) + 0.174 DERN - 0.332 DCUST LN (RPRS) is natural logarithm of the relative price of restricted stock expressed in percentage terms [(p*/p) • 100]. LN (REV), the natural logarithm of the firm's revenues (in millions); LN (RBRT), the natural logarithm of the restricted block relative to total common stock (in per cent); DERN, a dummy variable equal to one if the firm's earnings are positive and equal to zero otherwise; and DCUST, a dummy variable equal to one if there is a customer relationship between the investor and the firm issuing the restricted stock and zero otherwise.

12. Bajaj ( 2001) Discount = a + 0.40 x Fraction of Shares Issued -0.08 x Z-Score + 3.13 x Standard Deviation of Returns + b 4 x Registration Indicator.

13. Abbott (2004) DLOM (delisting change in value) = - 0.22220 +0.39571XCumexret +1.146XCap90X10^-5 +0.02491XTurnover

14. Models Considering lack of diversification but assuming Marketability and Liquidity Tabak Meulbroek

15. Tabak DLOM= 1-exponent ( σ s 2 / σ m 2 )XRPXT Discount for lack of diversification RP is the equity risk premium T is the time to liquidation

16. Meulbroek DLOM= 1-(1/(1+R)n) Where R is the product of the market risk premium multiplied by the difference between the asset’s beta and the ratio of standard deviation of returns for the asset and the market, a measure of incremental risk. ((σ s / σ m )- β )XRP

17. Models considering Delayed Liquidation as lack of Marketability QMDM Stockdale

18. DCF Models QMDM /Stockdale QMDM Framework The Expected Holding Period (HP) Expected Distribution Yield (D%) Expected Growth in Distributions (GD%) Projected Terminal Value Stockdale Enhancements

19. Stockdale explicitly accommodates inherent uncertainty in the estimated liquidation period. Assumes a linear liquidation probability, the model is flexible enough to accommodate any selected probability distribution. Allows for the starting point for the period of liquidation to be any time in future rather than the present time period

20. Time Volatility (Option) Models Black Scholes Put (BSP) (Chaffee 1993) Average Price Asian Put (AAP) (Finnerty 2002) Look Back Put (LBP) (Longstaff 1995) (Abbott 2007)

21. BSP Black Scholes Put (BSP) is a simple contract. It provides protection against any realized loss in value at maturity of the contract. (LOSS I) The minimum value any asset can reach is zero. Therefore, the maximum value payable under a BSP contract is the exercise price for the put.

22. BSP P(T) = e -rT N(-d2)- N (-d1) Where d1= [(r+σ2/ 2) T]/ σ  T And d2 = d1- σ  T The estimated BSP discount for lack of liquidity then becomes P(T)/[1+P(T)]

23. BSP Basics σ is the standard deviation for the returns computed for the same d1= [Lognormal(S/K) + (r+σ 2 / 2) T]/ σ  T d2 = d1- σ  T And N(-d1) and N(-d2) are the Normal cumulative distribution probabilities Setting S=K=1

24. Finnerty model :Asian Average Put D(T) = V[ e rt N(r/   T +  T / 2) –N (r/   T -  T / 2)] and  2 = σ 2 T + Ln [2( e σ2 T - σ 2 T -1)] - 2 Ln [ e σ2 T -1]

25. Finnerty Model Discount Once again setting V to 1, D(T) becomes [ e rt N(r/   T +  T / 2) – N (r/   T -  T / 2)] and the corresponding discount for lack of liquidity becomes D(T)/ 1+ D(T)

26. Look Back Put F ( V , T ) = V (2+ σ 2 T / 2) N (  σ 2 T /2) + V  ( σ 2 T /2  ) e (-σ2 T /8) - V

27. Look back Put DISCOUNT set V to 1, the LBP option premium becomes F ( T ) = (2+ σ 2 T / 2) N (  σ 2 T /2) +  (σ 2 T /2  ) e (- σ2 T /8) -1 the corresponding LBP discount for lack of liquidity becomes F ( T )/ (2+ σ 2 T / 2) N (  σ 2 T /2) +  (σ 2 T /2  ) e (- σ2 T /8)

28. Estimated DLOL Low Volatility (Annual σ 0.10-0.30), Low Risk free rate (3%), short duration (1 year)

29. Discounts Comparison 7.90% 20.81% 9.36% 0.3 7.71% 20.20% 9.04% 0.29 7.52% 19.60% 8.72% 0.28 7.33% 18.98% 8.40% 0.27 7.14% 18.36% 8.07% 0.26 6.94% 17.74% 7.74% 0.25 6.75% 17.10% 7.41% 0.24 6.55% 16.47% 7.08% 0.23 6.35% 15.82% 6.74% 0.22 6.16% 15.17% 6.41% 0.21 5.96% 14.52% 6.07% 0.2 5.76% 13.86% 5.72% 0.19 5.56% 13.19% 5.38% 0.18 5.37% 12.51% 5.03% 0.17 5.17% 11.83% 4.68% 0.16 4.97% 11.14% 4.33% 0.15 4.77% 10.45% 3.98% 0.14 4.58% 9.75% 3.63% 0.13 4.38% 9.04% 3.27% 0.12 4.19% 8.33% 2.92% 0.11 4.00% 7.61% 2.56% 0.1 AAP LBP BSP Annual Standard Deviation

30. Estimated DLOL Mid range Volatility (Annual σ . 0.40-0.60), Medium Risk free rate (6%), Medium duration (5 year)

31. 40.64% 61.52% 23.82% 0.6 40.39% 60.97% 23.47% 0.59 40.13% 60.42% 23.12% 0.58 39.86% 59.85% 22.76% 0.57 39.58% 59.27% 22.39% 0.56 39.30% 58.68% 22.02% 0.55 39.00% 58.08% 21.64% 0.54 38.69% 57.47% 21.26% 0.53 38.37% 56.84% 20.87% 0.52 38.04% 56.21% 20.47% 0.51 37.70% 55.56% 20.07% 0.5 37.36% 54.90% 19.66% 0.49 37.00% 54.23% 19.25% 0.48 36.63% 53.55% 18.83% 0.47 36.25% 52.85% 18.40% 0.46 35.86% 52.14% 17.97% 0.45 35.46% 51.41% 17.53% 0.44 35.06% 50.68% 17.09% 0.43 34.64% 49.92% 16.64% 0.42 34.22% 49.16% 16.18% 0.41 33.79% 48.38% 15.72% 0.4 AAP LBP BSP Annual Standard Deviation

32. Estimated DLOL for High Volatility (Annual σ . 0.70-0.90), High Risk free rate (9%), Long duration (10 year)

33. 59.63% 83.32% 23.72% 0.9 59.63% 83.06% 23.56% 0.89 59.63% 82.79% 23.39% 0.88 59.63% 82.52% 23.22% 0.87 59.63% 82.25% 23.04% 0.86 59.62% 81.97% 22.86% 0.85 59.62% 81.68% 22.68% 0.84 59.62% 81.38% 22.49% 0.83 59.62% 81.08% 22.29% 0.82 59.62% 80.78% 22.09% 0.81 59.61% 80.46% 21.89% 0.8 59.61% 80.14% 21.68% 0.79 59.61% 79.81% 21.46% 0.78 59.60% 79.48% 21.24% 0.77 59.60% 79.14% 21.02% 0.76 59.60% 78.79% 20.79% 0.75 59.59% 78.43% 20.55% 0.74 59.59% 78.06% 20.31% 0.73 59.58% 77.69% 20.07% 0.72 59.57% 77.30% 19.81% 0.71 59.57% 76.91% 19.56% 0.7 AAP LBP BSP Annual Standard Deviation

34. Thank you for joining us. Please remember to turn in your evaluation forms. Plan to join us next year for our Seventeenth Annual Conference.