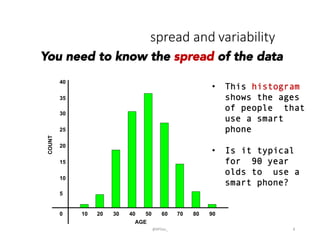
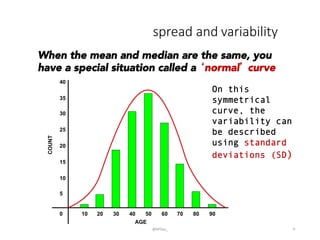
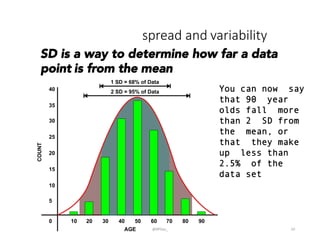
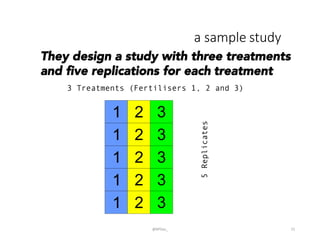
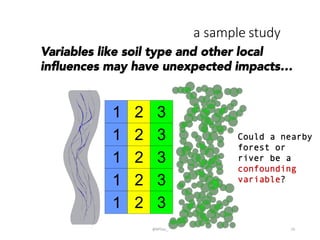
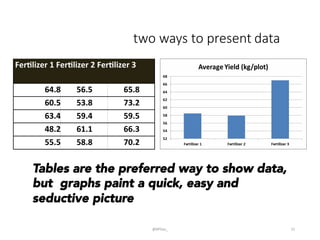
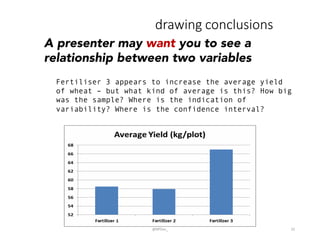
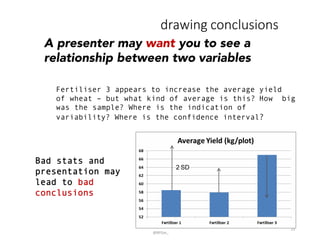
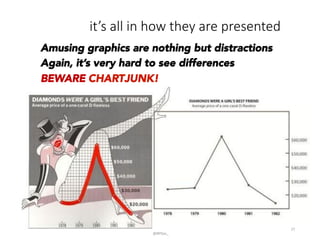
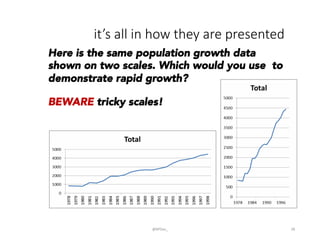
This document provides an introduction to descriptive statistics and how numbers can be used to describe data patterns but also be misused or misrepresented. It discusses how descriptive statistics are used to describe data distributions, find trends, determine if samples represent populations, and draw conclusions. However, it cautions that averages, variability, sample size, potential outliers, and confidence intervals must be considered to properly understand data. Graphs can also distort data if scales are manipulated or too much "chartjunk" is used. Skepticism is advised toward conclusions from data that lack appropriate context and statistical significance.

1. torturing numbers
a novice’s guide to descriptive dtatistics
1
Bandhu
P.
Das

2. "If you torture the data long
enough, it will confess"
@BPDas_
2
– Ronald Harry Coase

3. why do we torture numbers?
@BPDas_
3
q Describe the story
q Find trends in data
against variation
q Determine if a sample
represents a population
q Draw conclusions about the story

4. a tool called
‘descriptive statistics’
is used
@BPDas_
4

5. describing numbers
@BPDas_
5
25 people were asked what an
average person pay in tax?
What do these numbers tell you?
£45,000
£3,700
£10,000
£2,000
£2,000
£15,000
£3,000
£5,000
£3,700
£2,000
£10,000
£2,000
£2,000
£3,700
£2,000
£5,700
£2,000
£2,000
£3,700
£2,000
£5,000
£2,000
£5,000
£2,000
£2,000

6. describing numbers
@BPDas_
6
£2,000
Here is the same data ordered from greatest to
least and weighted to show how many times each
value occurs in the data set
• Now what do the data tell
you?
• What is the average income?
£45,000
£15,000
£10,000
£5,700
£5,000
£3,700
£3,000

7. £45,000
£15,000
£10,000
£5,700
£5,000
£3,700
£3,000
describing numbers
@BPDas_
7
BEWARE! The reported ‘average’ might
depend on what you are meant to see.
Which would you use?
MEAN (arithmetic average)
MEDIAN (midpoint in range)
MODE (most frequent)
So, to really understand the
data set you need more than
just the ‘average’
£2,000

8. spread and variability
@BPDas_
8
You need to know the spread of the data
• This histogram
shows the ages
of people that
use a smart
phone
• Is it typical
for 90 year
olds to use a
smart phone?

9. spread and variability
@BPDas_
9
When the mean and median are the same, you
have a special situation called a ‘normal’ curve
On this
symmetrical
curve, the
variability can
be described
using standard
deviations (SD)

10. spread and variability
@BPDas_
10
SD is a way to determine how far a data
point is from the mean
You can now say
that 90 year
olds fall more
than 2 SD from
the mean, or
that they make
up less than
2.5% of the
data set

11. spread and variability
@BPDas_
11
If we collapse the whole data set to one bar,
we can show the mean with some measure
of variability (std dev, std error, etc.)
Without some indication of variability, you
cannot effectively compare two data sets

12. spread and variability
@BPDas_
12
Min Q1 Median Q3 Max
Perhaps the best way to describe any data set is
with five numbers: Minimum, Q1, Median, Q3,
Maximum. This helps when comparing data sets,
and when there are oddities called outliers.
25% 25% 25% 25%
*

13. “79.48% of all statistics are
made up on the spot.”
@BPDas_
13
– John A. Paulos

14. a sample study
@BPDas_
14
Researchers want to
know which of three
fertilisers produce the
highest wheat yield in
kg/plot

15. a sample study
@BPDas_
15
They design a study with three treatments
and five replications for each treatment
3 Treatments (Fertilisers 1, 2 and 3)
5Replicates

16. a sample study
@BPDas_
16
Could a nearby
forest or
river be a
confounding
variable?
Variables like soil type and other local
influences may have unexpected impacts…

17. a sample study
@BPDas_
17
This is why a good study is
randomised, to defeat potentially
confounding variables

18. Does the sample
plot in our study
represent all the
wheat in all the
world?
P
O
P
U
L
A
T
I
O
N
SAMPLE
@BPDas_
18

19. uncertainty
@BPDas_
19
With all the unknown variables, there will
always be a degree of uncertainty that our
sample represents the population
That’s why the more samples we have, the more
confident we are that our study represents the
population

20. confidence
@BPDas_
20
• Any confidence interval
could be used, but 95% is
often chosen
• This means that 95% of
the time, you expect your
data represents reality
• BEWARE reports with no
confidence interval

21. @BPDas_
21
Fer$lizer
1
Fer$lizer
2
Fer$lizer
3
64.8
56.5
65.8
60.5
53.8
73.2
63.4
59.4
59.5
48.2
61.1
66.3
55.5
58.8
70.2
two ways to present data
Tables are the preferred way to show data,
but graphs paint a quick, easy and
seductive picture

22. drawing conclusions
A presenter may want you to see a
relationship between two variables
Fertiliser 3 appears to increase the average yield
of wheat – but what kind of average is this? How big
was the sample? Where is the indication of
variability? Where is the confidence interval?
@BPDas_
22

23. drawing conclusions
A presenter may want you to see a
relationship between two variables
Fertiliser 3 appears to increase the average yield
of wheat – but what kind of average is this? How big
was the sample? Where is the indication of
variability? Where is the confidence interval?
@BPDas_
23
Bad stats and
presentation may
lead to bad
conclusions
2 SD

24. drawing conclusions
@BPDas_
24
Correlation does not imply causation
The more firemen fighting a fire, the
bigger the fire is observed to be.
Therefore more firemen cause an increase
in the size of a fire

25. Often, a presenter wants to lead you to
a conclusion. Newspapers, TV and
online articles should be scrutinised!
BEWARE:
“This is not a scientific poll…”
“These results may not be representative of
the population”
“…based on a list of those that responded”
“Data showed a trend but was not
statistically significant”
it’s all in how they are presented
@BPDas_
25

26. it’s all in how they are presented
@BPDas_
26
Pies are for eating
It’s very hard to see differences
BEWARE CHARTJUNK!

27. it’s all in how they are presented
@BPDas_
27
Amusing graphics are nothing but distractions
Again, it’s very hard to see differences
BEWARE CHARTJUNK!

28. it’s all in how they are presented
@BPDas_
28
Here is the same population growth data
shown on two scales. Which would you use to
demonstrate rapid growth?
BEWARE tricky scales!

29. it’s all in how they are presented
@BPDas_
29
BEWARE statements with no context.
Here’s a made-up example:
Did you know that even speaking to
someone that once smoked, DOUBLES
your chance of getting cancer?! ;)
Your odds go from
to
0.000000001:1
0.000000002:1

30. conclusion
@BPDas_
30
Like any tool, stats can be misused
(intentionally or unintentionally)
Maintain a healthy skepticism and
question charts, tables and conclusions
where insufficient information is provided

31. references
@BPDas_
31
- The Cartoon Guide to Statistics (1993)
- Larry Gonick and Woolcott Smith
- How to Lie with Statistics (1954)
- Darrel Huff