This document discusses various temperature sensing techniques including P-N junction thermometers, IC temperature sensors, thermocouples, and resistive temperature sensors. It provides details on the principles and applications of different types of temperature sensors like diode thermometers, transistor thermometers, IC sensors like LM135 and AD590, thermocouples, platinum resistance thermometers, and thermistors. The document also covers topics like calibration of thermometers, interfacing temperature sensors, and conversion of thermal voltage to temperature.

1. 1
Interfacing Temperature Sensors
P-N Junction Thermometers
IC Temperature Sensors
Thermocouples
Calibration of Thermometers
Resistive Temperature Sensors
Other Temperature Measurement Techniques

2. Chap 0 2
Applications of temperature sensing
 Food industry
 Monitor temperature-time cycles to ensure high food
quality
 Automotive industry
 Combustion and exhaust temperature
 Solar Energy conversion
 Accurate temperature measurement to achieve optimal
heat flow
 Energy efficiency in the home and industry
 Measurement of temperature
 Hospital infant incubator
 Temperature must be kept in the proper range

3. Chap 0 3
Block Diagram of electronic
thermometer

4. Chap 0 4
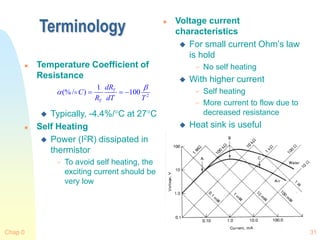
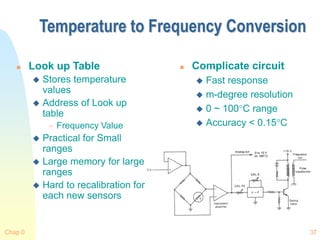
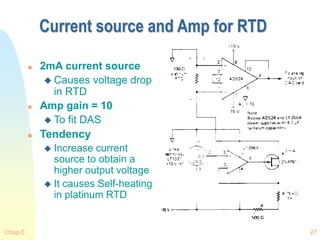
P-N Junction Thermometers
 Principle of Diode
Thermometer
 Forward Biased Current
 Voltage
 Where T is in K
 Voltage vs. Temperature
 Useful range
 40 ~ 400K
[exp( ) 1]
2
s
qV
I I
kT
 
4.6
(ln ln )
g
E kT
V M I
q q
  

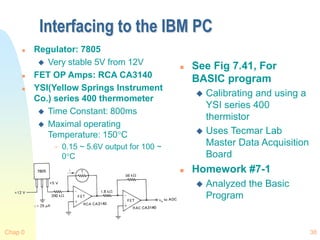
5. Chap 0 5
Diode thermometer with known
characteristics
 Motorola MTS 105
 Calibrate Diode to obtain
accurate output
 Constant Current source
must be very stable
 1C accuracy
 0.002K with precision
GaAs Diode
 Calibration Procedures
 Determine VBE at
extremes (-40C and
150C)
 Plot line using VBE(-40C) and
VBE(150C)

 Given VBE(Tx), Tx can be found
using curve from step 2 or
equation
 Diode are more sensitive and
linear than others
 Wide range
 Less repeatable
 Affected by Magnetic (>
2.25 0.003( 600) /
c BE
T V mV C
   
[ ( ) (25 )]/ 25
x BE x BE c
T V T V C T
  

6. Chap 0 6
Diode thermometer with Unknown
characteristics
 Diode must be
calibrated over the
desired range
 Using Table or Curves
 Changing temperature
(e.g., 0 ~ 50C)
 Recording Vi vs. Ti
 After calibrating, Tx
can be determined
using measure Vx and
Vi vs. Ti curve
 Interpolation
techniques are
needed
 Using Equation
 Linear regression
 T = a + bV
• Where a and b are
constant
• Can be determined
using
– Ti = a + bVi
 Tx can be determined
using measured Vx and
Equation
 Manufacturer provides
 Table or Curve
 Equation

7. Chap 0 7
Transistor as a Temperature Sensor
 Base-Emitter voltage of a
transistor varies directly
with temperature at a
constant collector current
 Thermometer using MTS 105
 R1 determine collector
current. Must be stable
 R2 is adjusted until Vo=0 for a
display in C
 Accuracy of 0.01C
 Range of –50 to 125C

8. Chap 0 8
BASIC Program for Transistor
Thermometers
 Calibrating and using the transistor thermometer
 For Tecmar Lab Master data acquisition Board
Initialize ADC
Select Channel 0
Start Conversion
Check EOC

9. Chap 0 9
C program for Calibrating and Using
the Transistor Thermometer
 For prototype board developed in Chapters 3, 4, and 5

10. Chap 0 10
IC Temperature Sensors
 Temperature sensing
circuit with output voltage
proportional to absolute
temperature

 If IC1/IC2 is constant
 VR1 is proportional to
temperature
 LX5700 from NS
 Range: -55 ~ 125C
 Sensitivity: 10mV/C
 Time Constant
 50 sec (Still Air)
 < 1 sec (Stirred Oil Bath)
 Output: 2.98V at 298K
 Accuracy: 3.8K
 Linearity: < 1K
 Not satisfactory in many
applications
 Poor Accuracy
1
1 2 1 2
2
ln( )
C
C BE BE
C
I
kT
R I V V
q I
  

11. Chap 0 11
IC Sensor: LM135, LM235, LM335
 Operate as two terminal Zenor
 Breakdown Voltage
proportional to absolute
temperature of +10mV/K
 When calibrated at 25C
 LM135 < 1.5C Error
 LM335 < 2C Error
 Range: -55 ~ 150C
 Output voltage:
 T0 is reference temperature
 Thermal Response time of LM335
Flowing Air
Still Air Stirred Oil Bath
0 0 0
0
( ) ( )
T
v T v T
T


12. Chap 0 12
IC Sensor: LM134-3, LM234-3, LM134-6, LM234-6
 IC temperature sensors with
current output
 Three terminal adjustable
current source
 Range
 -55 ~ 125C : LM134-3, 6
 -25 ~ 100C : LM234-3, 6
 Operate over wide voltage
 1 ~ 40V
 Accuracy
 3C : LM134-3, LM234-3
 6C : LM134-6, LM234-6
 Not for precision
temperature measurement
 Output current

 T: temperature in K
 i0 is programmable
 By adjusting R
 1 A ~ 10mA
0
(227 / )
V K T
i
R



13. Chap 0 13
IC Sensor: AD590
 Two terminal IC
temperature sensor
 Better accuracy and
linearity than LM135
 Current output depends
on absolute temperature
 Insensitive to the voltage
across it
 Used with long lead
wires
 VT: voltage across R
 If R=358,
 Error
 < 0.3C : AD590J
 < 0.05C: AD590M
 Time Constant
 60 sec (Still Air)
 1.4 sec (Stirred Oil)
 Operating Range
 -55 ~ 150C
 High Output Impedance
 > 10M
 Excellent rejection of
supplying voltage drift
and ripple
1
2
ln 179 ( )
T
I
kT
V T V
q I
 
1 /
T
I
A K
T



14. Chap 0 14
Thermocouples
 Thermocouple
is a two-wire
device
 Composed of
dissimilar
metals or
alloys with one
end welded
together
 Types of thermocouples

15. Chap 0 15
Type of thermocouple junctions
 Exposed junction
 Extending beyond the
protective metallic
sheath
 Fast Response
 Static or flowing non-
corrosive gas
 Ungrounded junction
 Insulated by MgO powder
 Suitable for corrosive
environment
 Grounded junction
 High pressure application
 For static or flowing
corrosive gas and liquid

16. Chap 0 16
Seebeck Effect: Principles of Thermocouples
 Two dissimilar metal or
alloy wires A and B joined
together at the end to form
a circuit
 If temperature are different
(T2 > T1), a current will flow
in circuit
 Seebeck thermal emf
 Emf(electromotive force)
producing above current
 Magnitude of thermal emf
can be measure using
Voltmeter or Ammeter

17. Chap 0 17
Principles of Thermocouples
 Broken at center
 Open loop circuit
voltage EAB
 Temperature
difference (T2 - T1)
 Composition of two
metal
 Example
 T2 = 0C , T1 = 1C
 T-type
 Copper + Constantan
 EAB = 39V
 S-type
 Platinum + Platinum-
10% rhodium
 EAB = 5V

18. Chap 0 18
Thermoelectric Laws
 Law of interior temperatures
 Emf is not affected by T3 and
T4
 Law of intermediate metals
 Emf is not affected by Metal
X if J1 and J2 are at the
same temperature
 Can solder or attach lead
wire
 Law of intermediate
temperature
 Can use reference table even
if reference junction is not
0C
 Law of Additive Emf
 Can create nonstandard
thermocouple combinations
and still use the reference
tables

19. Chap 0 19
Picking Up the Thermovoltage
 Directly connect voltmeter
to thermocouple
 Can not read thermal emf
 New thermal junction
• J2 : No emf
– Copper – copper
• J3 : emf V3
– Copper -
constantan
 The output of voltmeter
 Proportional to voltage
difference between V1
and V3
 To find T1, we must know
T3
 Put J3 in ice bath
• 0C
• V = function of T1

20. Chap 0 20
Cold junction compensation
 In practice, No need to put
J3 to ice bath
 Add Voltage to cancel V2
to zero
 Then output is directly
proportional to V1
 If TA increase
 VA increase with VA
 IA of AD590 also
increase
 AD590
• IC temperature sensor
 AD580
• 2.5V stable voltage
reference
 Most of IA flows through
RA
 Produce - VA which
cancels VA in cold
junction
 The output voltage Eo
 Eo  VT

21. Chap 0 21
Simpler approach using AD595
 Built in capacity
for
 Cold junction
compensation
 Fault detection
 Output voltage
 10mV/C

22. Chap 0 22
Conversion of Thermal Voltage to
Temperature
 Temperature Vs. Voltage
relationship
 Slightly Nonlinear
 To achieve accuracy
 Entire range must be
calibrated
 Manufacturer provide table
and curve
 Lookup table in computer
 Interpolation needed
 Large memory consumption
 Curve Fitting
 Power series polynomial
 Better accuracy as n
increases
2
0 1 2
n
n
T A AV A V A V
    

23. Chap 0 23
Calibration of Thermometers
 To ensure temperature
accuracy
 Noise Reduction of
thermocouples
 Output voltage is order
of V
 Sensitive to interface
 Analog active filter
and Guarding
techniques are
needed
 Thermal Time constant
 Depends on particular
mounting
arrangements
 Heat transfer
 Surrounding medium
 Generally, the smaller
the sensor, the faster it
will respond
 Generally
 Thermocouple: 550ms
• Exposed butt-welded
25m diameter: 3ms
• Time constant
increase with diameter
of wire and sheath
 Diode, Transistor: 10s

24. Chap 0 24
Resistive Temperature Sensors
 Resistance of materials are changed with
temperature
 Conductive materials
 Metals
 R increases as T increases
 Called RTD
• Resistance Temperature Detector
 Semiconductors
 R decreases as T increases
 Called Thermistors

25. Chap 0 25
Resistive Thermometers
 Nickel, Copper and Platinum is
most commonly used
 Resistance Vs. Temperature
curve
 Not linear
 Ro : R at 0C
 Simplified Equation

 Limited range (0 ~ 100C)
 Platinum is most widely
 Copper
 Low resistive
  need long wire
 Nickel
 Low cost
 Resistance Vs.
Temperature
2
0 1 2
(1 )
n
T n
R R a T a T a T
    
0 1
(1 )
T
R R a T
 

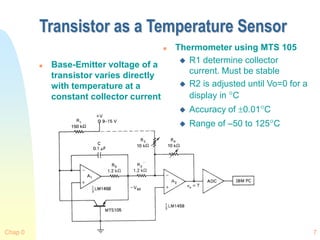
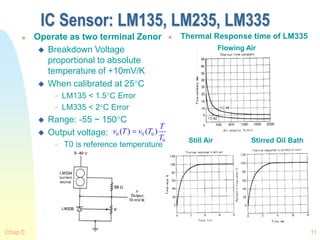
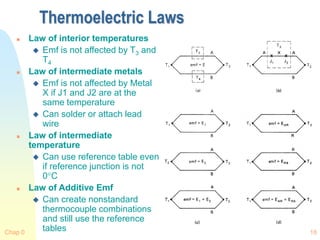
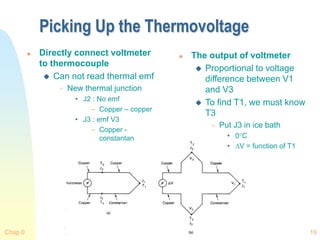
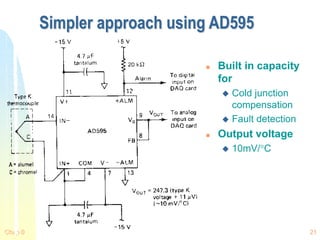
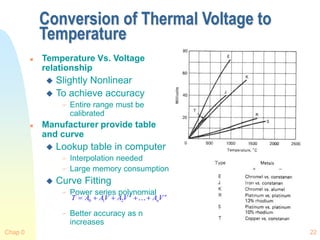
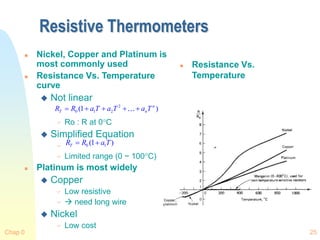
26. Chap 0 26
Platinum Thermometers
 SPRT
 Standard Platinum
Resistance
Thermometer
 Range
 13.81K ~ 903.89K
 Some are designed to
1050C
 Callendar-Van Dusen
Equation
 -183 ~ 630C Range
 Typically
0
3
[ (0.01 1)(0.01 )
(0.01 1)(0.01 ) ]
T
R R T T T
T T
 

  
 
1
0
0.00392
1.49
0( 0),0.11( 0)
100
C
T T
R






  
 

27. Chap 0 27
Current source and Amp for RTD
 2mA current source
 Causes voltage drop
in RTD
 Amp gain = 10
 To fit DAS
 Tendency
 Increase current
source to obtain a
higher output voltage
 It causes Self-heating
in platinum RTD

28. Chap 0 28
Types of Thermistor

29. Chap 0 29
Thermistors
 Comparison of NTC and
PTC thermistor and
platinum resistance
thermometer
 NTC
 Negative Temperature
Coefficient
 High sensitivity
 Highly nonlinear
 PTC
 Positive Temperature
Coefficient
 Inserting Barium and
Titanate mixtures
 Called switching
thermistors
 Switching temperature
(Curie Pont)
• -20 ~ 125C

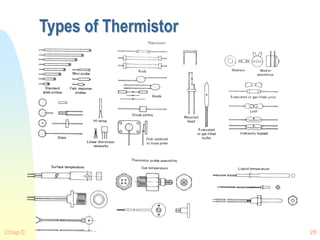
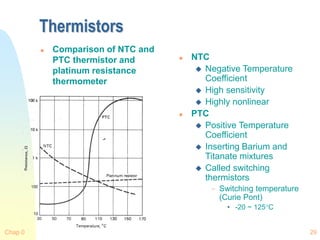
30. Chap 0 30
Empirical Correction
 Basic Characteristics
 Where
 Ro : R at known To
• Usually 298.15K
  : Material constant for
thermistor in K
• Determined from R
obtained at 0 and 50C
• 1500 ~ 6000K range
– Typically, 4000K
 Few  ~ 10M range
 Steinhart-Hart Equation
 Where
 A, B, C are found by
solving three equations
with known R and T
 Accuracy < 0.01C
 More narrow range
 -40C < T1, T2, T3 <150C,
|T2-T1|<50C, |T3-T2|<50C
0
0
1 1
exp[ ( )]
T
R R
T T

  3
1
ln (ln )
A B R C R
T
  
1
ln
B
C
T R A
 


31. Chap 0 31
Terminology
 Temperature Coefficient of
Resistance
 Typically, -4.4%/C at 27C
 Self Heating
 Power (I2R) dissipated in
thermistor
 To avoid self heating, the
exciting current should be
very low
 Voltage current
characteristics
 For small current Ohm’s law
is hold
 No self heating
 With higher current
 Self heating
 More current to flow due to
decreased resistance
 Heat sink is useful
2
1
(%/ ) 100
T
T
dR
C
R dT T

   

32. Chap 0 32
Applications
 Thermistor
Pneumography
 Used to obtain
breathing rate
 by detecting the
temperature
difference between
inspired cool air and
expired warm air
 Temperature measurement
 Simple circuit
 Battery + Thermistor +
Microammeter
 More sensitive circuit
 Differential circuit
 0.0005C change can be
indicated

33. Chap 0 33
Applications
 Temperature compensation
 To compensate for ambient
temperature change effects
on copper coils in meters,
generators and motors
 PTC of copper and NTC of
thermistor produce relatively
constant coil resistance for
changing ambient
temperature
 Liquid Level Measurement
 R of thermistor in air
 Decreases as heat up
 Enough current to close
relay
 R of thermistor in liquid
 Increases as cooling
 The relay will open

34. Chap 0 34
Applications
 Altimeter
 Called Hyposometer
 Sea level ~ 37500m
 With precision of better
than 1%
 Heat until liquid boils
 Measure R of thermistor
 R depends on pressure
 Pressure depends on
Altitude
 Power measurement
 R in bridge: 200
 Thermistor: 2K
 Thermistor heat up until 200
 Balance in bridge
 Calculate DC power
 Applying High Frequency
power
 R of thermistor more
decreases
 Reduce DC power until bridge
balance again
 Calculate DC power
 The difference of two DC
power is HF power

35. Chap 0 35
Linearization
 Using parallel resistors
 Choosing Rp
 Tm: Midscale temp.
 Rt,m: R at Tm
 More linear, Less
Sensitive:
 Using Series resistors
 Choosing Gs
 More Linear, Less
Sensitivity
,
2
2
m
P t m
m
T
R R
T





2
,
( / )
( / ) 1
m
P
t m P
T
R R

 

,
2
1
2
m
P t m
S m
T
G G
R T



 

2
,
( / )
( / ) 1
m
P
t m P
T
G R






36. Chap 0 36
Linearization
 Implementation of series
linearization using OP
Amps
 Minimal deviation of
linearity
 0.15C for 0 ~40C
 Temperature to Frequency
Conversion
 Hysteresis-based
oscillator
 Frequency of oscillation
nonlinearly depends on
temperature
 CPU counts frequency of
oscillator's output

37. Chap 0 37
Temperature to Frequency Conversion
 Look up Table
 Stores temperature
values
 Address of Look up
table
 Frequency Value
 Practical for Small
ranges
 Large memory for large
ranges
 Hard to recalibration for
each new sensors
 Complicate circuit
 Fast response
 m-degree resolution
 0 ~ 100C range
 Accuracy < 0.15C

38. Chap 0 38
Interfacing to the IBM PC
 Regulator: 7805
 Very stable 5V from 12V
 FET OP Amps: RCA CA3140
 YSI(Yellow Springs Instrument
Co.) series 400 thermometer
 Time Constant: 800ms
 Maximal operating
Temperature: 150C
 0.15 ~ 5.6V output for 100 ~
0C
 See Fig 7.41, For
BASIC program
 Calibrating and using a
YSI series 400
thermistor
 Uses Tecmar Lab
Master Data Acquisition
Board
 Homework #7-1
 Analyzed the Basic
Program

39. Chap 0 39
Other temperature measurement
techniques
 Ultrasonic Thin-wire Thermometer
 Velocity of sound depends on
temperature
 High temperature
 2000 ~ 3000C
 Maximal error: 30C
 Quartz-Crystal Thermometer
 Resonant frequency of quartz-crystal
oscillator is linearly related to
temperature
 Accuracy: 0.04C
 Range: -80 ~ 250C
 Johnson Noise Thermometer
 Noise voltage power density
spectrum is function of temperature
 Accuracy: 20C
 Range: 400 ~ 1770K
 Nuclear Quadrupole Resonance
Thermometer
 Nuclear quadrupole resonance
absorption frequency
decreases with increasing
temperature
 Accuracy : 1mK
 Range : 90 ~ 398K
 Eddy Current Thermometer
 Non Contacting temperature
measurement
 HF magnetic filed on steel 
Eddy current  New magnetic
field  Detecting coil
 The magnitude of eddy current
depends on temperature and
distance
 Accuracy : < 3C
 Range: 25 ~ 300C