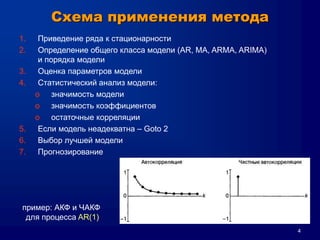
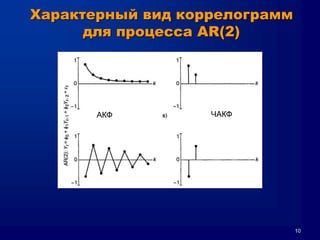
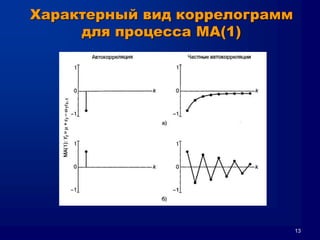
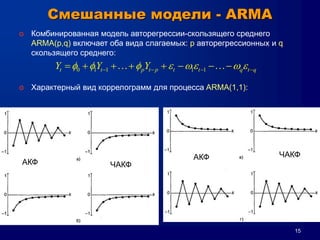
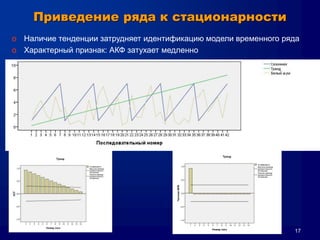
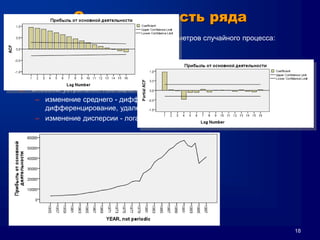
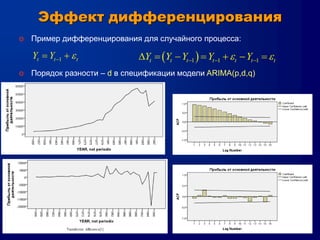
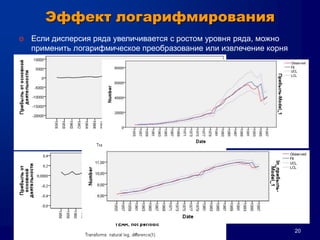
Документ описывает метод Box-Jenkins (ARIMA) для прогнозирования временных рядов, включая обобщенные концепции моделирования, оценки параметров и диагностические проверки. Он объясняет, как привести ряд к стационарности, методы авторегрессии и скользящего среднего, а также кривые автокорреляции и частичной автокорреляции. Кроме того, представлены критерии выбора модели и проблемы, которые могут возникнуть при анализе временных рядов.

1. Курс «Компьютерная
поддержка
прогнозирования»
Заходякин Глеб Викторович,
кафедра Информационных систем
и технологий в логистике
e-mail: postlogist@gmail.com

2. 2
Метод Бокса-Дженкинса (ARIMA)
o Общие принципы моделирования
o Модели авторегрессии и скользящего среднего
o Выборочная АКФ и ЧАКФ, статистики связанные
с ними
o Приведение ряда к стационарности
o Реализация стратегии разработки модели
o Сезонные модели ARIMA

3. 3
Общая характеристика метода
o Модели ARIMA (Auto-Regressive
Integrated Moving Average) – класс
универсальных линейных моделей
для описания стационарных и
нестационарных временных рядов
o Разработчики – G.P. Box,
G.M. Jenkins (197x-199x)
o Для моделирования используются
только данные временного ряда
o Разработаны расширения моделей –
ARIMAX, учитывающие факторы, выбросы
и структурные изменения различных видов
o Особенностью метода является итеративный подход к определению лучшей
модели среди всех возможных
o Для идентификации моделей используются диаграммы последовательности
ряда и коррелограммы с АКФ и ЧАКФ
o Для оценки адекватности применяется анализ остатков:
– остатки должны быть малыми
– не должно быть закономерных компонент и корреляций

4. 4
Схема применения метода
1. Приведение ряда к стационарности
2. Определение общего класса модели (AR, MA, ARMA, ARIMA)
и порядка модели
3. Оценка параметров модели
4. Статистический анализ модели:
o значимость модели
o значимость коэффициентов
o остаточные корреляции
5. Если модель неадекватна – Goto 2
6. Выбор лучшей модели
7. Прогнозирование
пример: АКФ и ЧАКФ
для процесса AR(1)

5. 5
Исследование автокорреляций
  
 
1
2
1
n
t t kt k
k n
tt
Y Y Y Y
r
Y Y
 

 




kr
tY t kY 
Y
- наблюдение в момент t - наблюдение с лагом (запаздыванием) в k периодов- наблюдение в момент t
- среднее значение временного ряда - коэффициент автокорреляции для лага k

6. 6
Оценка значимости rk
o Стандартная ошибка для rk:
o Доверительный интервал для rk: +/- t * SE(rk)
o Использование t-статистики:
o Критическое значение – t-распределение, df=n-1, a
 
1
2
1
1 2
1
k
i
i
k
r
SE r
nn



 

 
k
k
r
t
SE r


7. 7
Статистика Бокса-Пирса
o Q-Статистика Бокса-Пирса
(Льюнг, Бокс) - Ljung-Box Q
o Для проверки используется распределение Хи2 с m степенями свободы
(m-k) или p-значение (p-вероятность того, что Q будет иметь
наблюдаемую величину по случайным причинам)
o Малое p-значение – АКФ значимо отличается от нуля!
 
2
1
2
m
k
k
r
Q n n
n k
  



8. 8
Модели авторегрессии AR
o Авторегрессионная модель порядка p имеет вид:
оцениваемые коэффициенты в модели – f.
o Коэффициент f0 (константа) связан со средним ряда:
если значения ряда изменяются относительно нуля, или были
центрированы относительно среднего: Zt = Yt – Yср, то константа не
нужна
o Порядок модели можно определить с помощью графика ЧАКФ:
количество rkk > 0 равно порядку модели, АКФ быстро затухает
0 1 1 2 2t t t p t p tY Y Y Yf f f f       
 0 1 21 pf  f f f   

9. 9
Характерный вид коррелограмм
для процесса AR(1)

10. 10
Характерный вид коррелограмм
для процесса AR(2)
АКФ ЧАКФ

11. 11
o В таблице показаны последние данные ряда
o Для описания используется модель AR(2)
o Параметры:
o Прогноз:
Y(76) = 115.2 – 0.535*(72) + 0.055*(99) = 77.2
Как применять модель
Период Время Факт
t-5 71 90
t-4 72 78
t-3 73 87
t-2 74 99
t-1 75 72
t 76 ?
0 1 1 2 2t t t tY Y Yf f f     
0 1 2115.2, 0.535, 0.0055f f f   

12. 12
Модель скользящего среднего MA
o Модель скользящего среднего порядка q задается уравнением:
 – постоянное среднее процесса, оцениваемые параметры – w
o Значение прогноза определяется значением ошибок прогноза в
предыдущих периодах, а не значением самой величины
o Название «скользящее среднее» относится к отклонению Yt от
среднего значения, представляющее собой линейную комбинацию q
ошибок (подобно скользящему окну в методе скользящего среднего):
1 1 2 2t t t t q t qY   w w  w        
Период Время Факт Прогноз Остаток
t-5 71 90 76.1 13.9
t-4 72 78 69.1 8.9
t-3 73 87 75.3 11.7
t-2 74 99 72 27
t-1 75 72 64.3 7.7
t 76 ?
1 1 2 2
(2):
75.4 0.5667 7.7
0.3560 27 80.6
t t t t
MA
Y   w  w      
   
  
1 1 2 2t t t t q t qY   w w  w        

13. 13
Характерный вид коррелограмм
для процесса MA(1)

14. 14
Характерный вид коррелограмм
для процесса MA(2)
ЧАКФАКФ

15. 15
Смешанные модели - ARMA
o Комбинированная модель авторегрессии-скользящего среднего
ARMA(p,q) включает оба вида слагаемых: p авторегрессионных и q
скользящего среднего:
o Характерный вид коррелограмм для процесса ARMA(1,1):
0 1 1 1 1t t p t p t t q t qY Y Yf f f  w w           
АКФ ЧАКФ
АКФ ЧАКФ

16. 16
Вид коррелограмм
для различных процессов
Модель АКФ ЧАКФ
AR(p) Затухает Обрывается на шаге p
MA(q) Обрывается на шаге q Затухает
ARMA(p,q) Затухает Затухает

17. 17
Приведение ряда к стационарности
o Наличие тенденции затрудняет идентификацию модели временного ряда
o Характерный признак: АКФ затухает медленно

18. 18
Стационарность ряда
o Стационарность означает постоянство параметров случайного процесса:
– среднего
– дисперсии
– вида распределения
o «Сильная» стационарность – нормальность распределения
o Способы устранения нестационарности:
– изменение среднего - дифференцирование и сезонное
дифференцирование, удаление тренда
– изменение дисперсии - логарифмирование или степенное преобразование

19. 19
Эффект дифференцирования
o Пример дифференцирования для случайного процесса:
o Порядок разности – d в спецификации модели ARIMA(p,d,q)
1t t tY Y    1 1 1t t t t t t tY Y Y Y Y         

20. 20
Эффект логарифмирования
o Если дисперсия ряда увеличивается с ростом уровня ряда, можно
применить логарифмическое преобразование или извлечение корня

21. 21
Критерии выбора модели
o Информационный критерий Акаике (Akaike Information Criterion, AIC):
o Байесовский информационный критерий Шварца (Bayesian Information
Criterion, BIC)
o Число параметров в модели, включая константу – r
o Оба критерия содержат слагаемое штрафа за увеличение числа
параметров
2
lnAIC MSE r
n
 
ln
ln
n
BIC MSE r
n
 