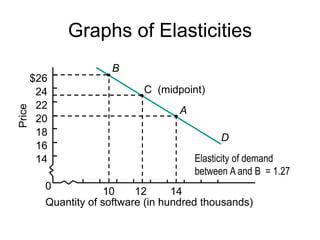
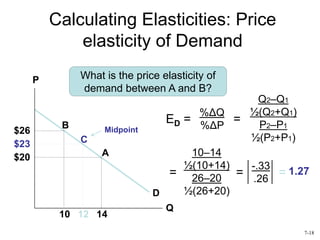
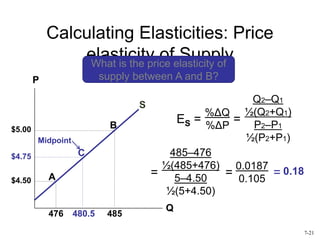
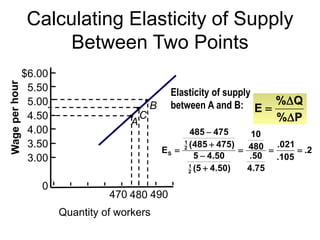
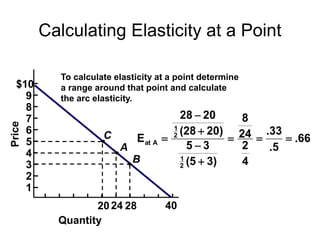
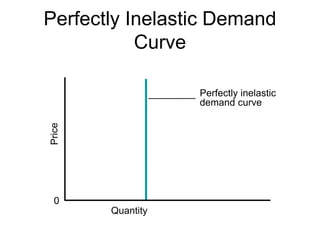
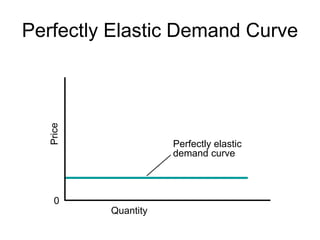
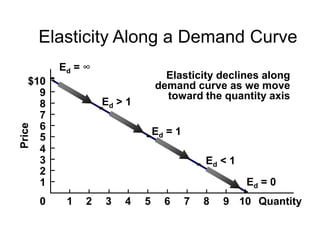
This document discusses the concept of elasticity in economics. It defines elasticity as a measure of responsiveness of one variable to another. Price elasticity of demand is the percentage change in quantity demanded divided by the percentage change in price. Demand is elastic if the quantity changes more than price and inelastic if quantity changes less than price. The document provides examples of calculating elasticity between points on demand and supply curves. It also discusses how elasticity changes along straight-line curves and is influenced by the availability of substitutes.

1. The Elasticity of Demand
Chapter 7

2. The Concept of Elasticity
• Elasticity is a measure of the
responsiveness of one variable to another.
• The greater the elasticity, the greater the
responsiveness.

3. Laugher Curve
Q. What’s the difference between an
economist and a befuddled old man with
Alzheimer’s?
A. The economist is the one with a
calculator.

4. The Concept of Elasticity
• Elasticity is a measure of the
responsiveness of one variable to another.
• The greater the elasticity, the greater the
responsiveness.

5. Price Elasticity
• The price elasticity of demand is the
percentage change in quantity demanded
divided by the percentage change in price.
price
in
change
Percentage
demanded
quantity
in
change
Percentage
=
ED

6. Sign of Price Elasticity
• According to the law of demand, whenever
the price rises, the quantity demanded
falls. Thus the price elasticity of
demand is always negative.
• Because it is always negative, economists
usually state the value without the sign.

7. What Information Price
Elasticity Provides
• Price elasticity of demand and supply
gives the exact quantity response to a
change in price.

8. Classifying Demand and Supply
as Elastic or Inelastic
• Demand is elastic if the percentage
change in quantity is greater than the
percentage change in price.
E > 1

9. Classifying Demand and Supply
as Elastic or Inelastic
• Demand is inelastic if the percentage
change in quantity is less than the
percentage change in price.
E < 1

10. Elastic Demand
• Elastic Demand means that quantity
changes by a greater percentage than the
percentage change in price.

11. Inelastic Demand
• Inelastic Demand means that quantity
doesn't change much with a change in
price.

12. Defining elasticities
• When price elasticity is between zero and
-1 we say demand is inelastic.
• When price elasticity is between -1 and
- infinity, we say demand is elastic.
• When price elasticity is -1, we say demand
is unit elastic.

13. Elasticity Is Independent of
Units
• Percentages allow us to have a measure
of responsiveness that is independent of
units.
• This makes comparisons of
responsiveness of different goods easier.

14. Calculating Elasticities
• To determine elasticity divide the
percentage change in quantity by the
percentage change in price.

15. The End-Point Problem
• The end-point problem – the percentage
change differs depending on whether you
view the change as a rise or a decline in
price.

16. The End-Point Problem
• Economists use the average of the end
points to calculate the percentage change.
 
 
2
1
1
2
1
2
1
2
P
+
P
)
P
-
(P
Q
Q
)
Q
-
(Q
=
Elasticity
½
½ 

17. Graphs of Elasticities
Quantity of software (in hundred thousands)
$26
24
22
20
18
16
14
0
D
B
A
10 12 14
C (midpoint)
Elasticity of demand
between A and B = 1.27

18. Calculating Elasticities: Price
elasticity of Demand
D
P
Q
What is the price elasticity of
demand between A and B?
$20
10
$26
14
Midpoint
B
A
ED =
%ΔQ
%ΔP
Q2–Q1
½(Q2+Q1)
P2–P1
½(P2+P1)
=
C
12
$23
=
10–14
½(10+14)
26–20
½(26+20)
-.33
.26
= 1.27
=
7-18

19. Price Elasticity: Supply
• Price elasticity of supply is the
percentage change in quantity supplied
divided by the percentage change in
• This tells us exactly how quantity supplied responds to
a change in price
ES =
• Elasticity is independent of units
% change in Quantity Supplied
% change in Price
7-19

20. Price Elasticity: Supply
• Supply is elastic if the percentage
change in quantity is greater than the
percentage change in price
Elastic supply is when ES > 1
• Supply is inelastic if the percentage change in quantity
is less than the percentage change in price
Inelastic supply is when ES < 1
7-20

21. Calculating Elasticities: Price
elasticity of Supply
P
Q
What is the price elasticity of
supply between A and B?
$4.50
476
$5.00
485
B
A
ES =
%ΔQ
%ΔP
Q2–Q1
½(Q2+Q1)
P2–P1
½(P2+P1)
=
=
485–476
½(485+476)
5–4.50
½(5+4.50)
Midpoint
C
480.5
$4.75
0.0187
0.105
= 0.18
=
S
7-21

22. Graphs of Elasticities
Elasticity of supply
between A and B = 0.18
Quantity of workers
$6.00
5.50
5.00
4.50
4.00
3.50
3.00
0
C
B
A
470
(midpoint)
480 490

23. Calculating Elasticity
)
P
P
(
P
P
)
Q
Q
(
Q
Q
P
%
Q
%
E
2
1
2
1
1
2
2
1
2
1
1
2









24. Calculating Elasticity of Demand
Between Two Points
27
.
1
26
.
33
.
23
6
12
4
)
20
26
(
20
26
)
10
14
(
14
10
E
2
1
2
1
D 









Quantity of software (in hundred thousands)
$26
24
22
20
18
16
14
0
Demand
B
A
10 12 14
C
midpoint
Elasticity of demand
between A and B: P
%
Q
%
E




25. Calculating Elasticity of Supply
Between Two Points
P
%
Q
%
E



Quantity of workers
$6.00
5.50
5.00
4.50
4.00
3.50
3.00
0
C
B
A
470 480 490
Elasticity of supply
between A and B:
2
.
105
.
021
.
75
.
4
50
.
480
10
)
50
.
4
5
(
50
.
4
5
)
475
485
(
475
485
E
2
1
2
1
S 








26. Calculating Elasticity at a Point
• Let us now turn to a method of calculating
the elasticity at a specific point, rather than
over a range or an arc.

27. Calculating Elasticity at a Point
• To calculate elasticity at a point, determine
a range around that point and calculate
the arc elasticity.

28. Calculating Elasticity at a Point
Quantity
$10
9
8
7
6
5
4
3
2
1
C
B
A
24 40
28
20
 
 
0.66
3
+
5
3)
-
(5
20
28
20)
-
(28
=
A
at
E 

½
½

29. Calculating Elasticity at a Point
Quantity
$10
9
8
7
6
5
4
3
2
1
C
B
A
24 40
28
20
To calculate elasticity at a point determine
a range around that point and calculate
the arc elasticity.
66
.
5
.
33
.
4
2
24
8
)
3
5
(
3
5
)
20
28
(
20
28
E
2
1
2
1
A
at 








30. Elasticity and Demand Curves
• Two important points to consider:
– Elasticity is related (but is not the same as)
slope.
– Elasticity changes along straight-line demand
and supply curves.

31. Calculating Elasticity at a Point
6 12 18 30 36 42 48 Quantity
8
7
6
5
4
3
2
1
$10
9
A
24 60
54
D
B
C
Supply
EA = 2.33
EB = 0.11
Demand
EC = 0.75
ED = 0.86

32. Elasticity and Demand Curves
• Two important points to consider:
– Elasticity is related (but is not the same as)
slope.
– Elasticity changes along straight-line demand
and supply curves.

33. Elasticity Is Not the Same as
Slope
• The steeper the curve at a given point, the
less elastic is supply or demand.
• There are two limiting examples of this.

34. Elasticity Is Not the Same as
Slope
• When the curves are flat, we call the
curves perfectly elastic.
• The quantity changes enormously in
response to a proportional change in price
(E = ).

35. Elasticity Is Not the Same as
Slope
• When the curves are vertical, we call the
curves perfectly inelastic.
• The quantity does not change at all in
response to an enormous proportional
change in price (E = 0).

36. Perfectly inelastic
demand curve
0
Quantity
Perfectly Inelastic Demand
Curve

37. Perfectly elastic
demand curve
Perfectly Elastic Demand Curve
0
Quantity

38. Demand Curve
Shapes and Elasticity
• Perfectly Elastic Demand Curve
– The demand curve is horizontal, any change in price can and
will cause consumers to change their consumption.
• Perfectly Inelastic Demand Curve
– The demand curve is vertical, the quantity demanded is totally
unresponsive to the price. Changes in price have no effect on
consumer demand.
• In between the two extreme shapes of demand curves
are the demand curves for most products.

39. Demand Curve
Shapes and Elasticity

40. Elasticity Changes Along
Straight-Line Curves
• Elasticity is not the same as slope.
• Elasticity changes along straight line
supply and demand curves–slope does
not.

41. Elasticity Along a Demand Curve
Price
$10
9
8
7
6
5
4
3
2
1
0 1 2 3 4 5 6 7 8 9 10 Quantity
Elasticity declines along
demand curve as we move
toward the quantity axis
Ed = 1
Ed = 0
Ed < 1
Ed > 1
Ed = ∞

42. The Price Elasticity of Demand Along a
Straight-line Demand Curve

43. Substitution and Elasticity
• As a general rule, the more substitutes a
good has, the more elastic is its supply
and demand.

44. Substitution and Demand
• The less a good is a necessity, the more
elastic its demand curve.
• Necessities tend to have fewer substitutes
than do luxuries.

45. Substitution and Demand
• Demand for goods that represent a large
proportion of one's budget are more elastic
than demand for goods that represent a
small proportion of one's budget.

46. Substitution and Demand
• Goods that cost very little relative to your
total expenditures are not worth spending
a lot of time figuring out if there is a good
substitute.
• It is worth spending a lot of time looking for
substitutes for goods that take a large
portion of one’s income.

47. Substitution and Demand
• The larger the time interval considered, or
the longer the run, the more elastic is the
good’s demand curve.
– There are more substitutes in the long run
than in the short run.
– The long run provides more options for
change.

48. Determinants of the
Price Elasticity of Demand
• The degree to which the price elasticity of
demand is inelastic or elastic depends on:
– How many substitutes there are
– How well a substitute can replace the good or
service under consideration
– The importance of the product in the
consumer’s total budget
– The time period under consideration