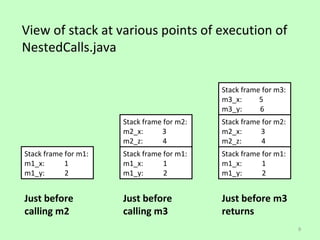
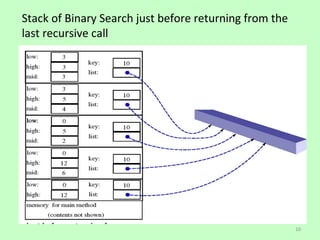
The document discusses recursion and binary search algorithms. It provides examples of using recursion to implement a binary search method. The method takes a list and key as parameters and recursively searches halves of the list to find the position of the key. Helper methods are used to encapsulate the recursive calls and base cases. The document also compares recursion to iteration, showing how recursion uses memory overhead by pushing method frames on a stack for each call.

1. More on Recursion
More techniques
1

2. Binary search algorithm
• Binary searching for a key in an array is similar to
looking for a word in dictionary
• Take the midpoint of the dictionary and see if the
key is in the lower half or upper half
• Pick the half the contains the key and take the
midpoint of the half and see which quarter the
key is in
• Repeat the above step until the key is matched or
the dictionary cannot be halved any more
2

3. Use helper method
• Given int[] list and int key
• You are asked to return
– the position of key in the array if matched or
– -1 if not matched
• What additional information do you need to
apply the algorithm above?
3

4. /** Use binary search to find the key in the list */
public static int recursiveBinarySearch(int[] list, int key) {
int low = 0;
int high = list.length - 1;
return recursiveBinarySearch(list, key, low, high); // use helper method
}// recursiveBinarySearch method
/** Use binary search to find the key in the list between list[low] and list[high] */
public static int recursiveBinarySearch(int[] list, int key, int low, int high)
{
if (low > high) // The list has been exhausted without a match
return -1;
int mid = (low + high) / 2;
if (key < list[mid])
return recursiveBinarySearch(list, key, low, mid - 1);
else if (key == list[mid])
return mid;
else
return recursiveBinarySearch(list, key, mid + 1, high);
}// recursiveBinarySearch method
4

5. What is the difference between:
public static int recursiveBinarySearch(
int[] list, int key){ . . . }
and
public static int recursiveBinarySearch(
int[] list, int key, int low, int high) { . . . }
The first method calls the second method.
Is it recursive call?
5

6. Recursion versus iteration
Iteration Recursion
• Uses for or while loop for • Recursion achieves
repetition but no recursion repetition without a loop
• Price paid: memory
overhead and run time
(Every time a method is
called, some space in
memory must be reserved
or allocated to
store the method’s local
• Why use recursion? variables and formal
parameters, if any)
6

7. public class NestedCalls {
public static void m1() {
int m1_x = 1;
int m1_y = 2;
m2(); // m1 calls m2
} // m1 method
public static void m2() {
int m2_ = 3;
int z = 4;
z = m3(); //m2 calls m3
}// m2 method
public static int m3() {
int m3_x =5;
int m3_y = 6;
return 1;
}//m3 method
}//NestedCalls class
7

8. Run NestedCalls.java with Bluej
Debugger
Observe the stack memory and
calling sequences
8

9. View of stack at various points of execution of
NestedCalls.java
Stack frame for m3:
m3_x: 5
m3_y: 6
Stack frame for m2: Stack frame for m2:
m2_x: 3 m2_x: 3
m2_z: 4 m2_z: 4
Stack frame for m1: Stack frame for m1: Stack frame for m1:
m1_x: 1 m1_x: 1 m1_x: 1
m1_y: 2 m1_y: 2 m1_y: 2
Just before Just before Just before m3
calling m2 calling m3 returns
9

10. Stack of Binary Search just before returning from the
last recursive call
10

11. Why use recursion?
In some problems, iterative solutions are hard to
find.
But recursion is easy - See the Towers of Hanoi
problem in textbook. Animation by Michael Iverson
11

12. Other problems that are neatly solved by recursion:
Fractals:
• The Koch snowflake (demo)
• Sierpinski triangle (demo)
12