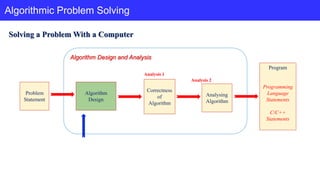
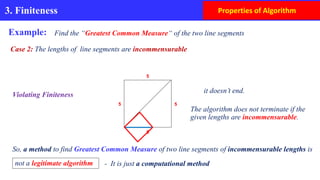
The document discusses the definition and properties of algorithms. It defines an algorithm as a sequence of unambiguous instructions to solve a problem within a finite amount of time. The key properties of algorithms discussed are: inputs, outputs, finiteness (terminating in a finite number of steps), definiteness (unambiguous instructions), effectiveness, and generality. Examples are provided to illustrate these properties, such as Euclid's algorithm for finding the greatest common divisor.