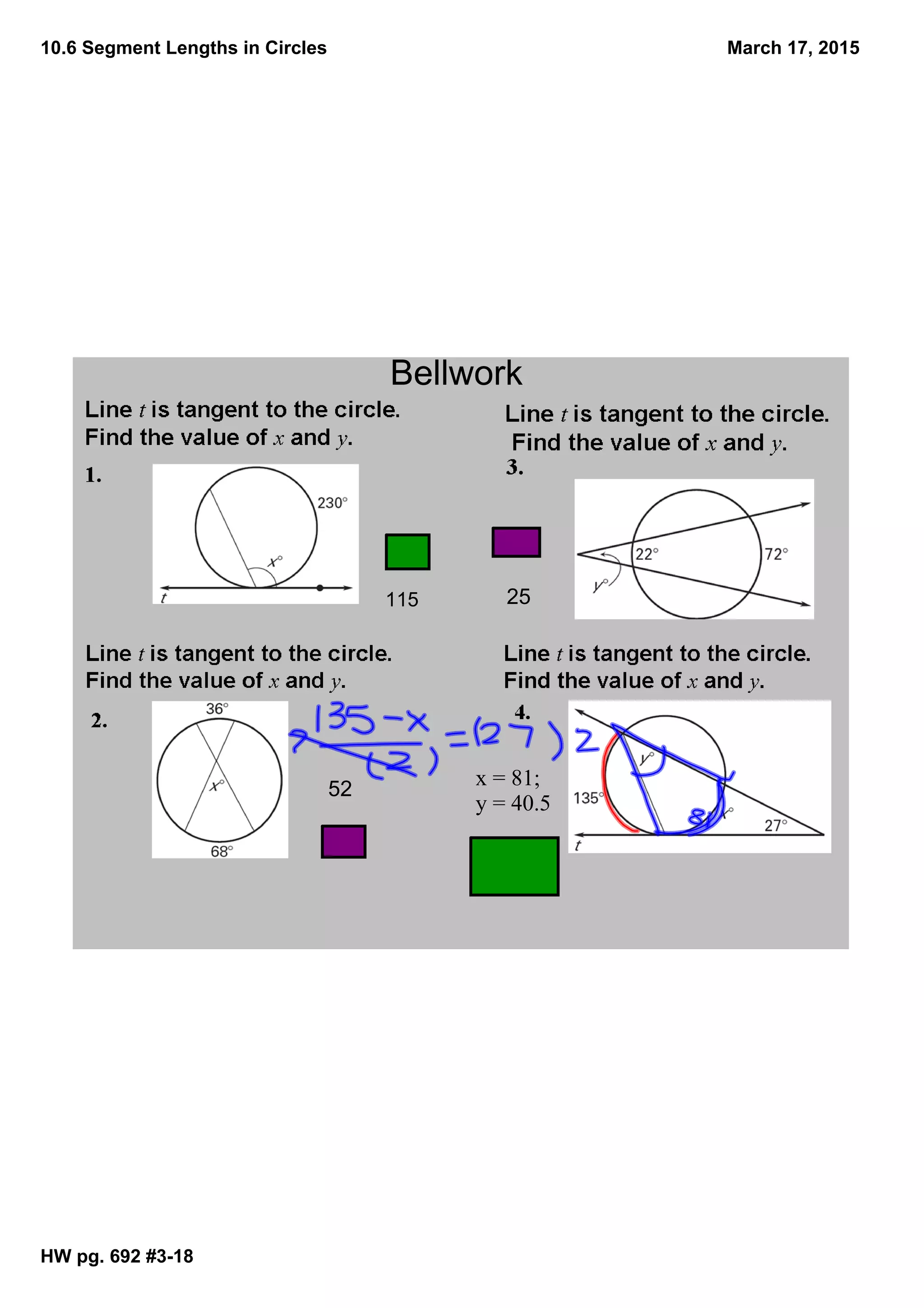
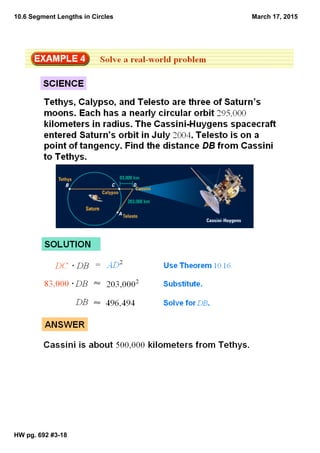
The document discusses different types of segments that can be formed from chords and secants intersecting inside or outside a circle. It defines segments of chords as parts of intersecting chords inside a circle, and explains that the product of the lengths of one chord equals the product of the other. It also defines secant segments, external segments, and tangent segments, and states theorems involving the proportional relationships between lengths of these segments.

1. 10.6 Segment Lengths in Circles
HW pg. 692 #3­18
March 17, 2015
Bellwork
115
52
25
x = 81;
y = 40.5

2. 10.6 Segment Lengths in Circles
HW pg. 692 #3­18
March 17, 2015
10.6 Segments Lengths in Circles
Segments of the chord: 2 chords intersected inside the circle
Segments of Chords: If 2 chords intersect inside circle, then the
product of lengths of 1 chord = product of length of other chord
C
B
E
A
D
EA * EB = EC * ED
Proportional?

3. 10.6 Segment Lengths in Circles
HW pg. 692 #3­18
March 17, 2015
Secant Segment: contains chord and has exactly one endpoint outside circle
External Segment: part of secant that is outside circle
secant segment
external segment
tangent segment
Segments of Secants Theorem:If 2 secant segments share same endpoint outside circle,
then the product of the lengths of 1 secant segment and its external segment =
product of lengths of other secant segment and its external segment.
E
A
B
D
C
EA * EB = EC * ED

4. 10.6 Segment Lengths in Circles
HW pg. 692 #3­18
March 17, 2015
Segments of Secants & Tangents Theorem: If a secant seg. & tangent seg.
share endpoint outside circle, then lengths of secant seg. * its external
segment = (length of tangent seg)2
E
C
D
A
EA2 = EC * ED

5. 10.6 Segment Lengths in Circles
HW pg. 692 #3­18
March 17, 2015

6. 10.6 Segment Lengths in Circles
HW pg. 692 #3­18
March 17, 2015
10.6 HW
pg. 692 #3‐18