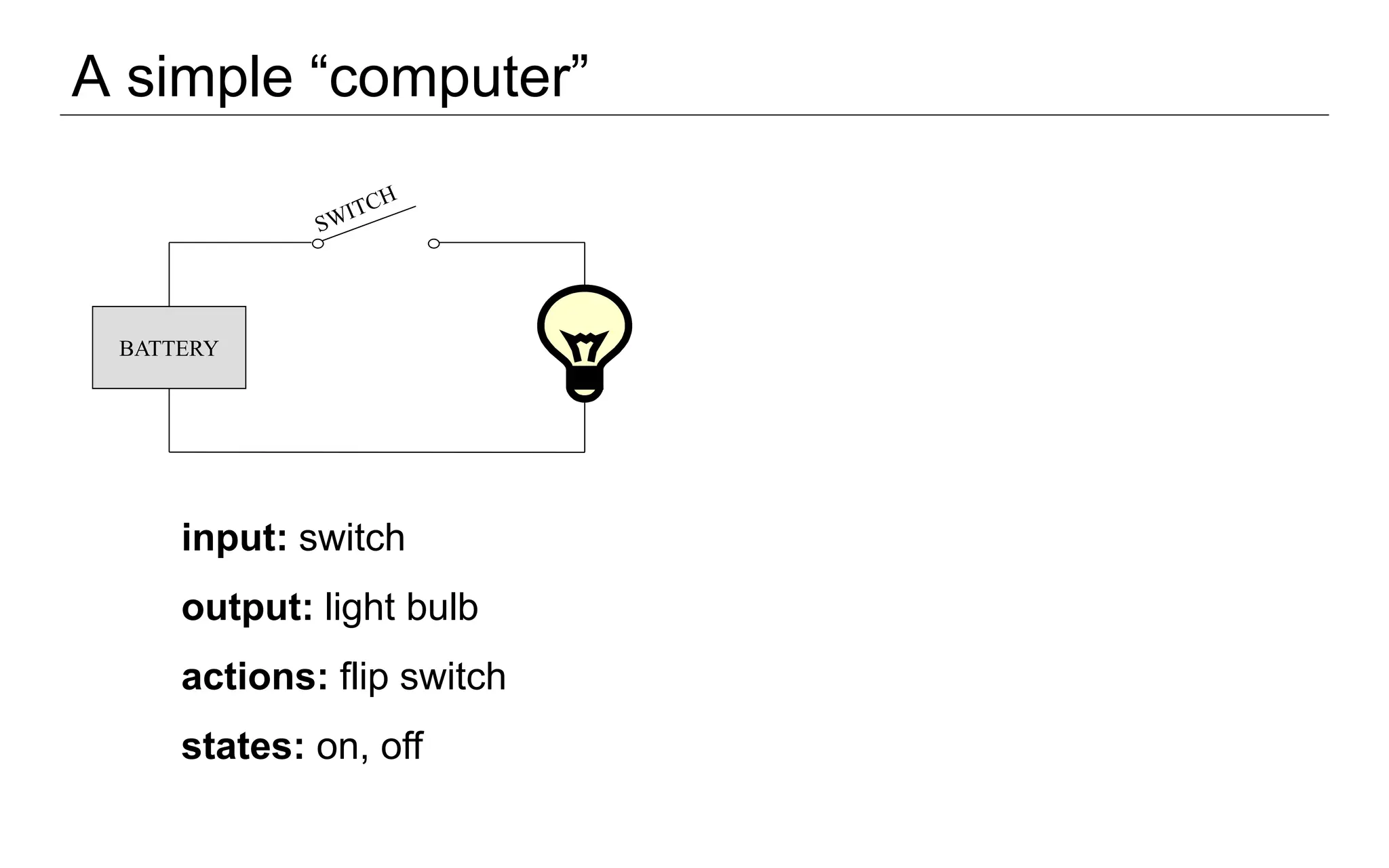
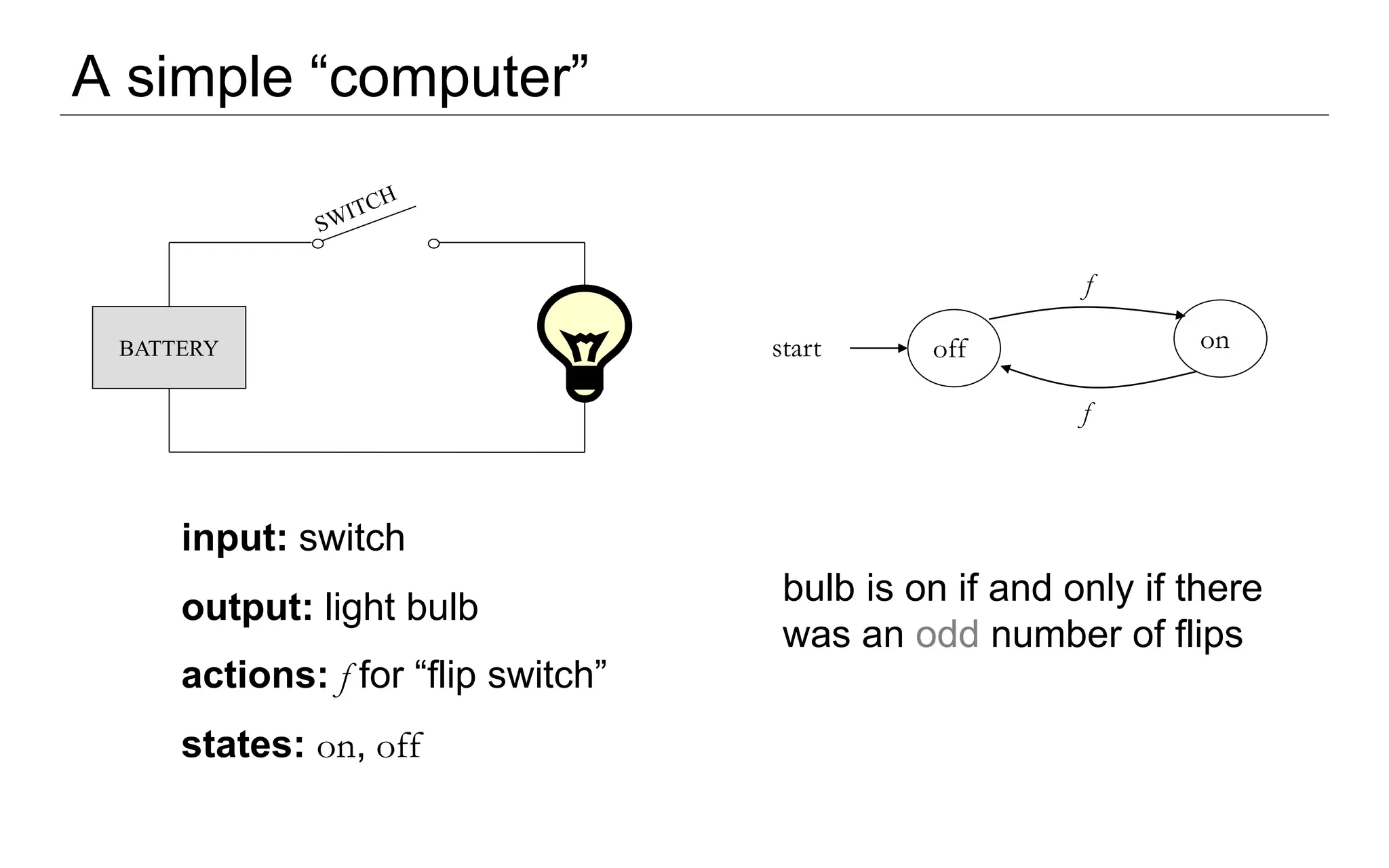
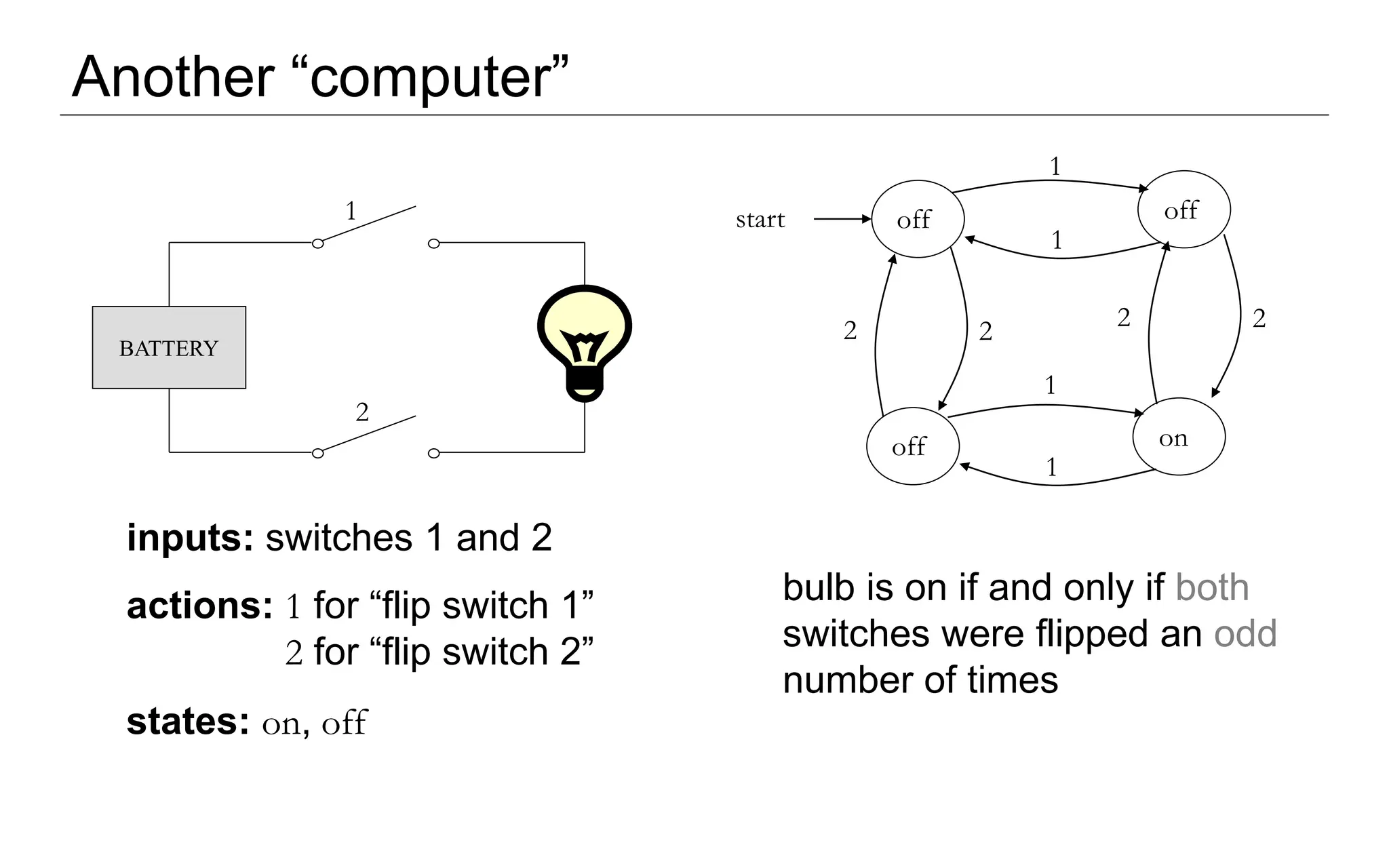
This document introduces formal language and automata theory. It defines key concepts like symbols, alphabets, and strings. An alphabet is a finite set of symbols, and a string is a finite sequence of symbols from an alphabet. Formal languages are sets of strings, and examples are given like the set of even-digit strings. Automata theory studies abstract computational devices and questions like what problems a given type of device can solve. Different automata are introduced, like finite automata and pushdown automata. The reading assignment covers mathematical preliminaries needed for the study of formal languages and automata.

1. Automata and complexity Theory

2. Chapter 1
Introduction

3. Definitions
• Symbol – An atomic unit, such as a digit, character,
lower-case letter, etc. Sometimes a word. [Formal
language does not deal with the “meaning” of the
symbols.]
• Alphabet – A finite set of symbols, usually denoted by
Σ.
Σ = {0, 1} Σ = {0, a, 4} Σ = {a, b, c, d}
• String – A finite length sequence of symbols,

4. Alphabets and strings
• A common way to talk about words, number, pairs of words,
etc. is by representing them as strings
• To define strings, we start with an alphabet
• Examples
An alphabet is a finite set of symbols.
S1 = {a, b, c, d, …, z}: the set of letters in English
S2 = {0, 1, …, 9}: the set of (base 10) digits
S3 = {a, b, …, z, #}: the set of letters plus the
special symbol #
S4 = {(, )}: the set of open and closed brackets

5. Strings
• The empty string will be denoted by e (epsilon)
• Examples
A string over alphabet S is a finite sequence
of symbols in S.
abfbz is a string over S1 = {a, b, c, d, …, z}
9021 is a string over S2 = {0, 1, …, 9}
ab#bc is a string over S3 = {a, b, …, z, #}
))()(() is a string over S4 = {(, )}

6. Let: u=ε w = 0110 y = 0aa x = aabcaa z = 111
concatenation: wz = 0110111
length: |w| = 4 |x| = 6 but |u| = 0
reversal: yR = aa0
Some special sets of strings
• Σ* All strings of symbols from Σ
• Σ+ Σ* - {ε}
Example: Σ = {0, 1}
• Σ* = {ε, 0, 1, 00, 01, 10, 11, 000, 001,…}
• Σ+ = {0, 1, 00, 01, 10, 11, 000, 001,…}
Strings

7. What is Formal Language ?
i.e. any subset L of Σ*
• Classes of formal languages (e.g., regular, context-free,
context-sensitive, recursive, recursively enumerable).
• Formal languages are related to programming
languages and natural languages
A (formal) language is a set of strings over an alphabet.

8. Formal Language Examples:
Σ = {0, 1}
L = {x | x is in Σ* and x contains an even number of
0’s}
Σ = {0, 1, 2,…, 9, .}
L = {x | x is in Σ* and x forms a finite length real
number}
= {0, 1.5, 9.326,…}
Σ = {a, b, c,…, z, A, B,…, Z}
L = {x | x is in Σ* and x is a CPP reserved word}

9. Formal Language Examples:
Σ = {CPP reserved words} U { (, ), ., :, ;,…} U {Legal
CPP identifiers}
L = {x | x is in Σ* and x is a syntactically correct CPP
program}
Σ = {English words}
L = {x | x Σ* and x is a syntactically correct English
sentence}

10. What is automata theory ?
• Automata theory is the study of abstract computational
devices
• Abstract devices are (simplified) models of real
computations
• Computations happen everywhere: On your laptop, on your
cell phone, in nature, …
• Why do we need abstract models?

11. A simple “computer”
BATTERY
input: switch
output: light bulb
actions: flip switch
states: on, off

12. A simple “computer”
BATTERY off on
start
f
f
input: switch
output: light bulb
actions: f for “flip switch”
states: on, off
bulb is on if and only if there
was an odd number of flips

13. Another “computer”
BATTERY
off off
start
1
inputs: switches 1 and 2
actions: 1 for “flip switch 1”
actions: 2 for “flip switch 2”
states: on, off
bulb is on if and only if both
switches were flipped an odd
number of times
1
2
1
off on
1
1
2 2 2 2

14. Another Example
• A state diagram for a simple Game Enemy model
Wander - player is with in sight - Attack
Attack - player is out of sight - Wander
Attack - player is attacking - Evade
Evade - player is idle - Attack

15. Different kinds of automata
• This was only some examples of a computational device,
and there are others
• We will look at different devices, and look at the following
questions:
– What can a given type of device compute, and what are its
limitations?
– Is one type of device more powerful than another?

16. Some devices we will see
finite automata Devices with a finite amount of memory.
Used to model “small” computers.
push-down automata Devices with infinite memory that can be
accessed in a restricted way.
Used to model parsers, etc.
Turing Machines Devices with infinite memory.
Used to model any computer.

17. Preliminaries of automata theory
• How do we formalize the question
• First, we need a formal way of describing the problems that
we are interested in solving
Can device A solve problem B?

18. Problems
• Examples of problems we will consider
– Given a word s, does it contain the subword “fool”?
– Given a number n, is it divisible by 7?
– Given a pair of words s and t, are they the same?
– Given an expression with brackets, e.g. (()()), does every left
bracket match with a subsequent right bracket?
• All of these have “yes/no” answers.
• There are other types of problems, that ask “Find this” or
“How many of that” but we won’t look at those.

19. Reading Assignment
• Mathematical Preliminaries
– sets,
– relations,
– functions,
– sequences,
– graphs,
– trees.