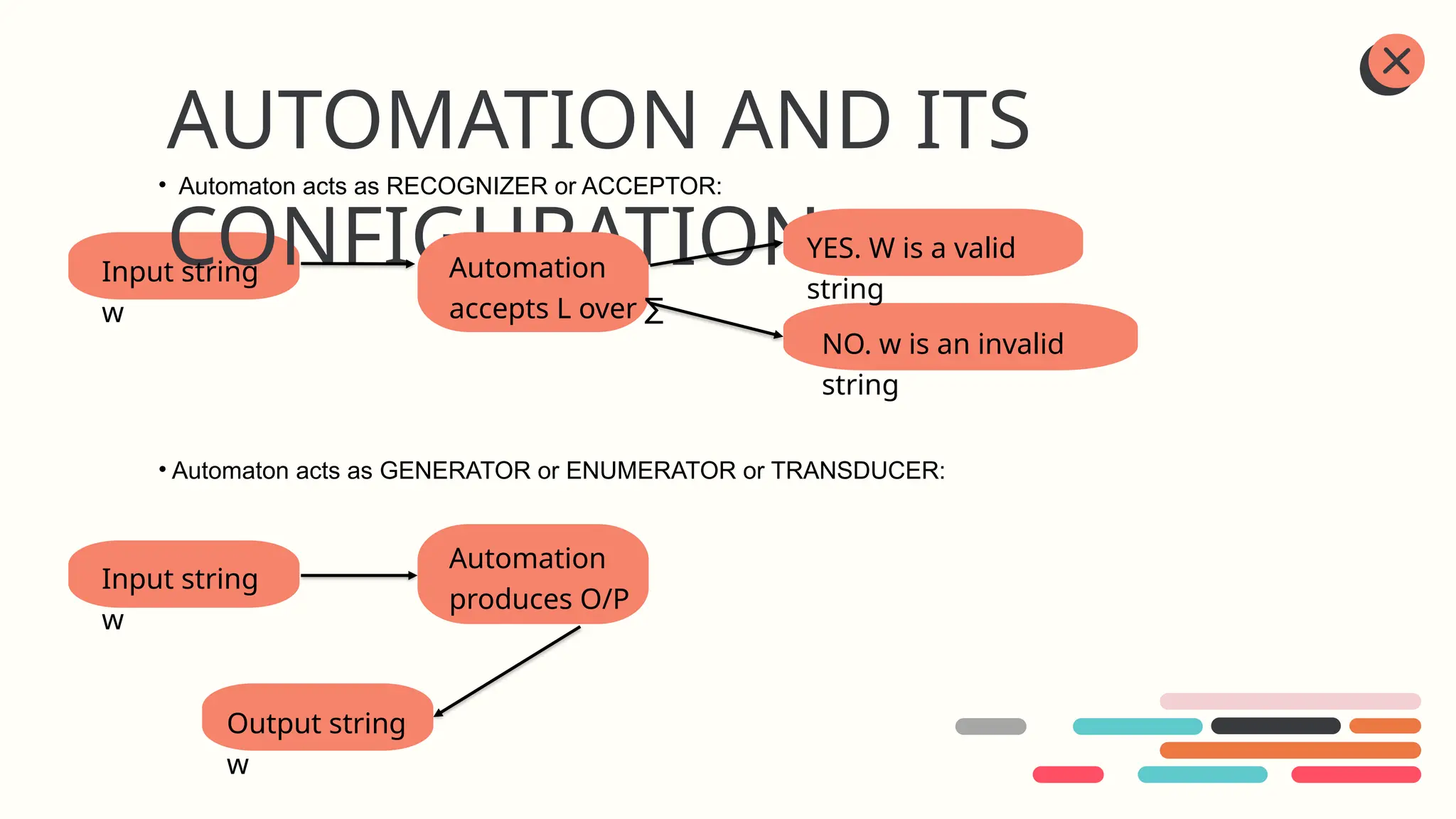
Automata theory is a branch of computer science focused on abstract computing devices called automata, which compute functions and solve problems through a series of states. The Turing machine is the most powerful type of automaton, serving as a model for modern computation. Key concepts include alphabets, strings, concatenation, and finite automata, which can be categorized as acceptors or transducers.

1. Automata
Theory and
Formal
Languages
LESSON 1

2. INTRODUCT
ION
• Automata Theory is an exciting and a theoretical
branch of Computer Science.
• Automaton = an abstract computing device.
• Simply stated, automata theory deals with the logic of
computation with respect to simple machines, referred
to as automata.
• Through automata, computer scientists can understand
how machines compute functions and solve problems.

3. ALAN TURING
(1912-1954)
A pioneer to Automata Theory
• Father of modern computer
• An English Mathematician
• Turing's machine is essentially an
abstract model of modern-day computer
execution and storage.

4. AUTOMATA
• Automatons are abstract models of machines.
• It perform computations on an input by moving through a series of
states or configurations.
• As a result, once the computation reaches an accepting
configuration, it accepts that input. The most general and powerful
automata is the Turing machine.
• Objective: To analyze the dynamic behavior of discrete systems.
• Characteristics of such machines are based on:
Inputs, Outputs & States.

5. • Automaton acts as RECOGNIZER or ACCEPTOR:
AUTOMATION AND ITS
CONFIGURATION
Input string
w
Automation
accepts L over ∑
YES. W is a valid
string
NO. w is an invalid
string
• Automaton acts as GENERATOR or ENUMERATOR or TRANSDUCER:
Input string
w
Automation
produces O/P
Output string
w

6. The Basic Concepts of
Automata Theory
ALPHABET:
• It is a finite, non-empty sets of Symbols.
• Representation: ∑ (sigma)
• Examples:
Binary Symbols: ∑ = {0,1}
All lower case letters: [= {a,b,c,..z}
Digits: [= {0,1,2,..9}
Alphanumeric: ∑ = {a-z, A-Z, 0-9}

7. The Basic Concepts of
Automata Theory
continuation
STRINGS:
• A string or word is a finite collection of symbols selected from
the alphabets (∑).
• A string can be empty, which is represented by ε ("Epsilon").
Length of String: The "Length" of the string is denoted by |w|
and it is the number of positions for the symbol in the string. For
example:
w = 01101 has length = 5 i.e |w| = 5

8. The Basic Concepts of
Automata Theory
continuation
EMPTY STRING:
• The "empty" string is the string with zero occurrence of symbols.
The empty string is represented by ε.
∑*= {ε, 0, 1, 01, 10, 000, 010, 0000,.....}
{0}*={ε, 0, 00, 000,0000,……..}
{1}*={ε,1,11,111,1111,…….}
Note that:
ε is in ∑*, regardless of what alphabet ∑ is.
i.e ε is only string whose length is 0.

9. The Basic Concepts of
Automata Theory
continuation
CONCATENATION OF STRINGS:
• Let x and y be two strings. Then xy denotes the concatenation
of x and y i.e, the string formed by making a copy of x and
followed it by a copy of y. Example: if x=ab & y=cd then
concatenation: xy=abcd.
REVERSE OF THE STRING:
• Reverse of the string can be achieved by simply interchanging
over last symbols. For example: w= abc, then (w)R = cba.

10. The Basic Concepts of
Automata Theory
continuation
POWERS OF ALPHABET:
Let ∑ be the alphabet. Then power of alphabet is given by:
• ∑k = the set of all strings of length k
• ∑* = ∑0 U ∑1 U ∑2 U …
• ∑+ = ∑1 U ∑2 U ∑3 U

11. The Basic Concepts of
Automata Theory
continuation
LANGUAGES:
L is said to be the language over a given set of alphabets, if L
belongs to ∑*.
For example:
1. L is a language that comprises of set of even numbers over the
alphabet
∑= {0,1}.
2. The language of all strings consisting of n 0's followed by n 1's,
for some n>=0: {ε, 01, 0011, 000111,....}

12. Key Points
• Finite Automata (FA) is also known as Finite State Machine
(FSM).
• Types of Finite Automata:
i. FINITE ACCEPTOR (FA without Output)
ii. FINITE TRANSDUCER (FA with Output)
• In case of ε-NFA, it has the capability of changing the state
without reading the input symbol.
• Model Configuration of Automaton:

13. THANK
YOU!