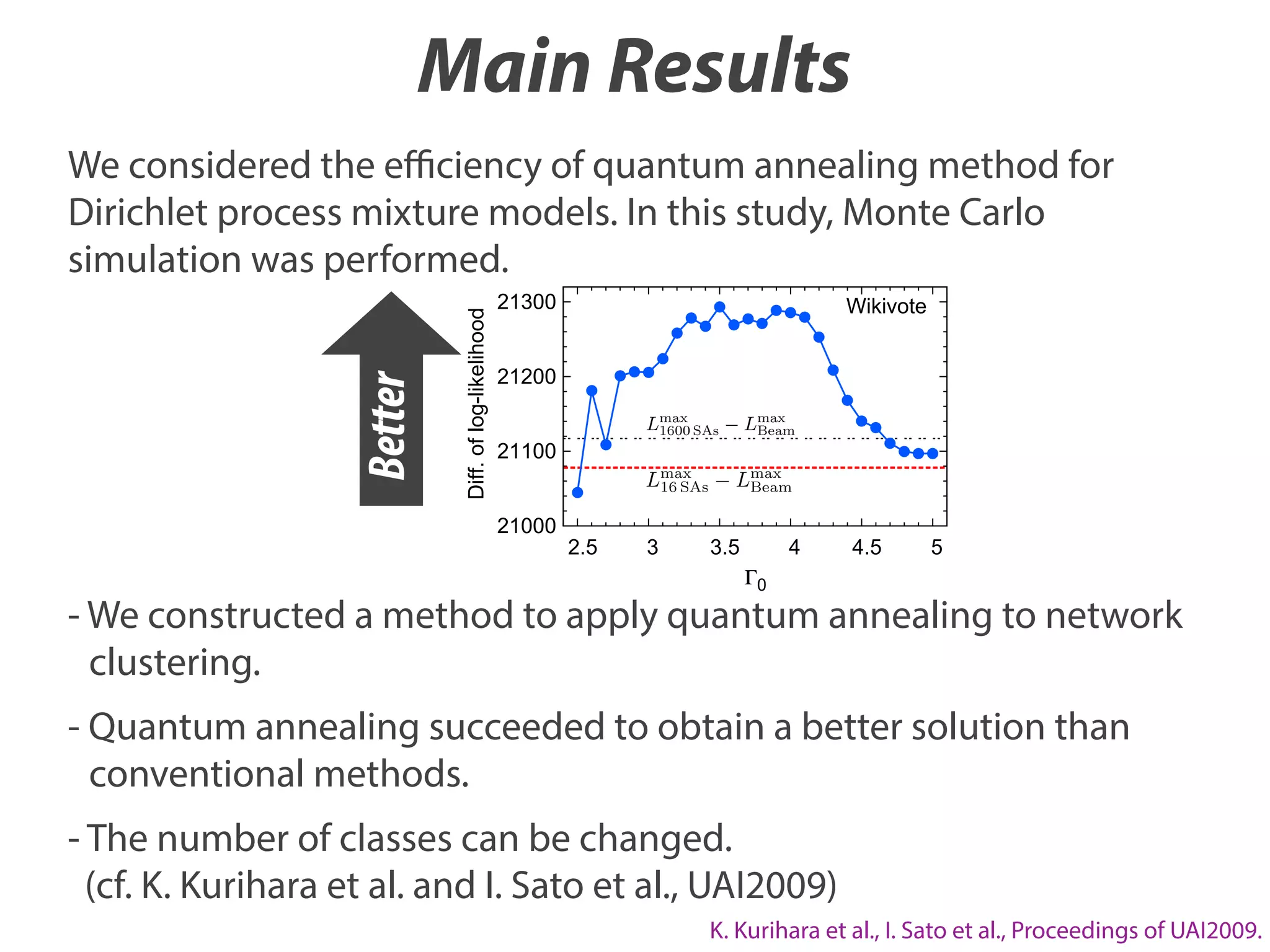
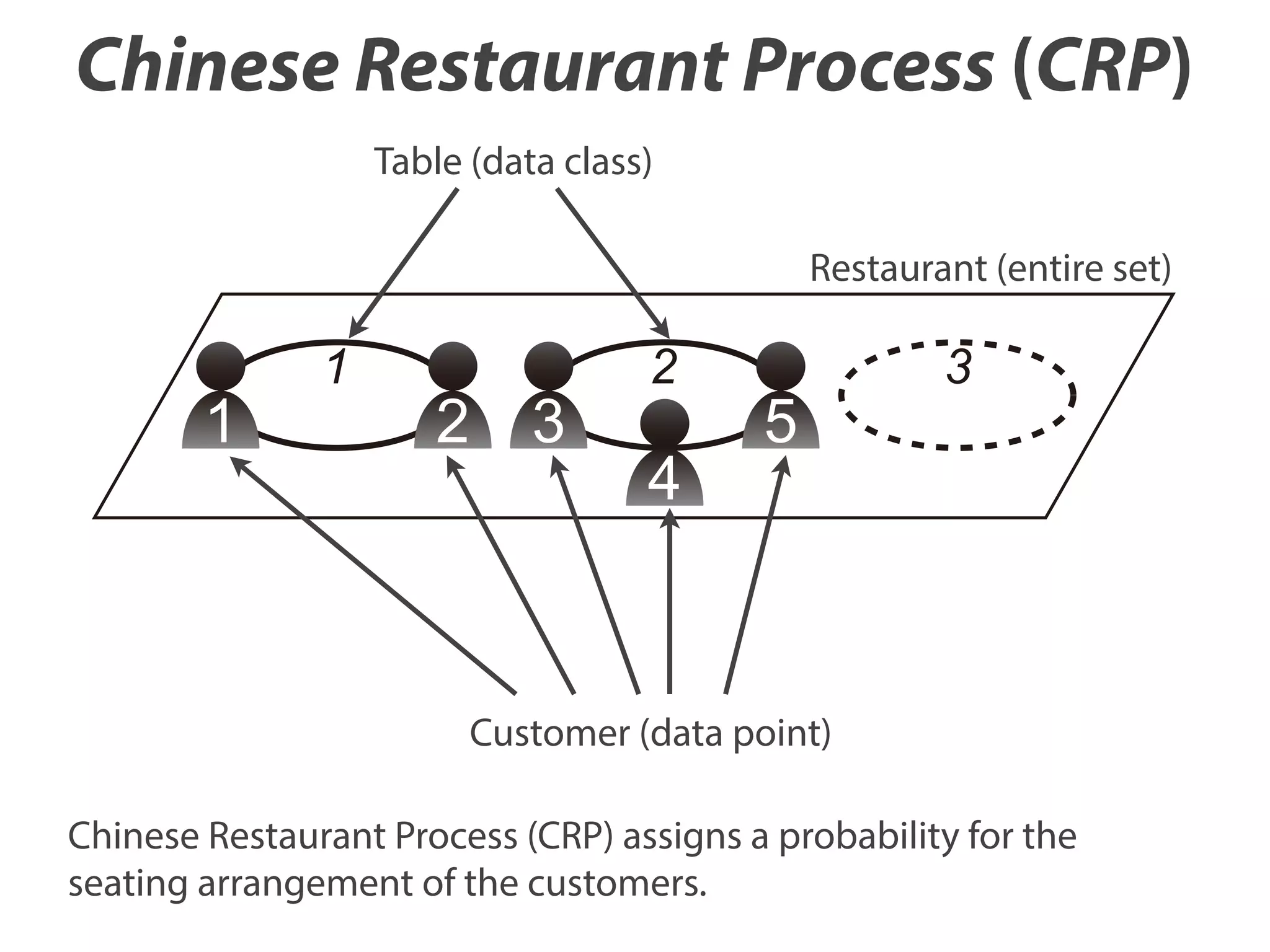
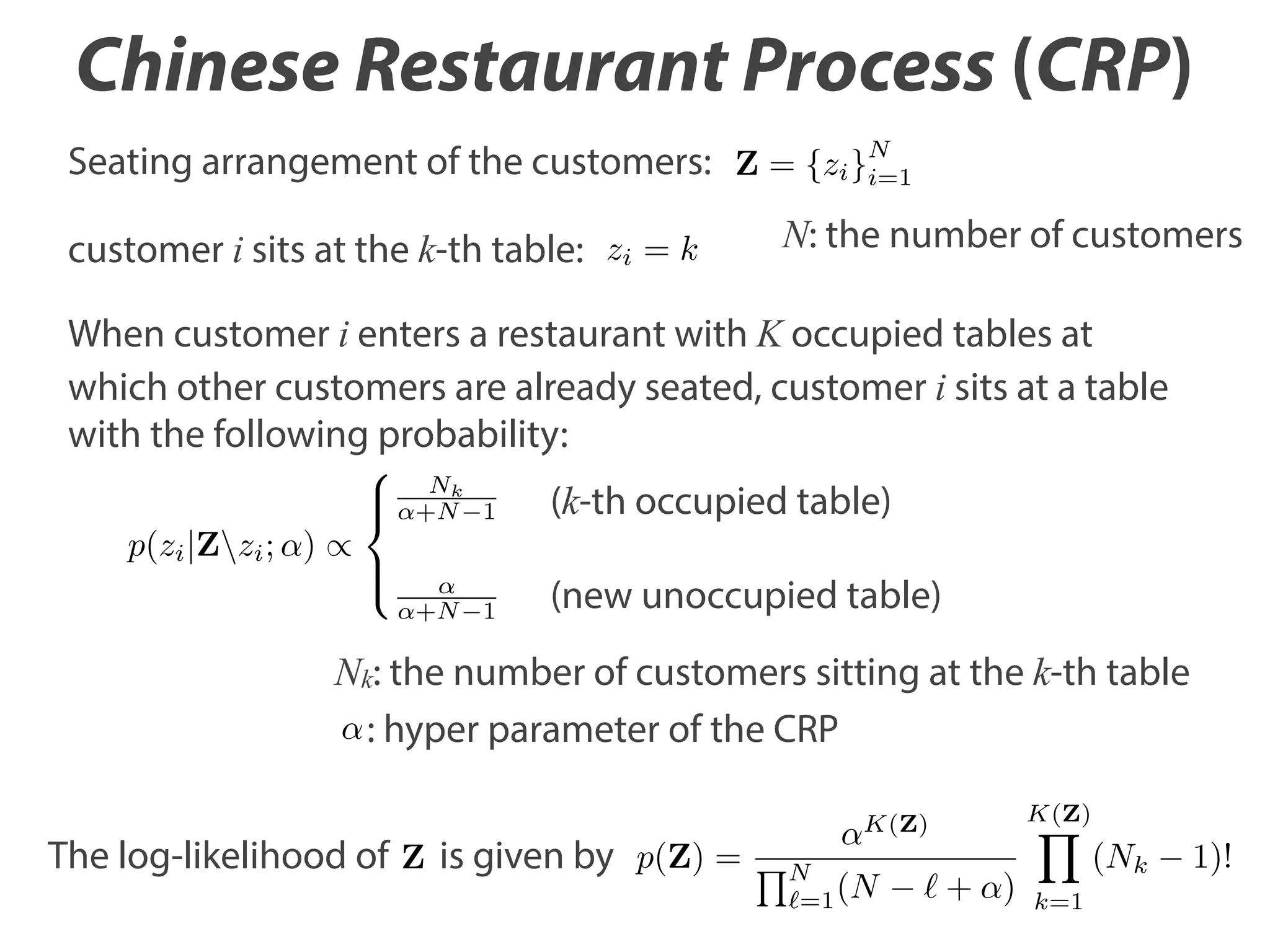
The document discusses the application of quantum annealing to Dirichlet process mixture models for network clustering, showing that this method yields better solutions than conventional techniques. It details the background optimization problems and introduces a new framework called QACRP (Quantum Annealing for Chinese Restaurant Process), which utilizes multiple 'restaurants' for improved seating arrangements of data points. The study validates the effectiveness of quantum annealing through Monte Carlo simulations applied to various network datasets.

1. Quantum Annealing for Dirichlet Process Mixture
Models with Applications to Network Clustering
Issei Sato, Shu Tanaka, Kenichi Kurihara,
Seiji Miyashita, and Hiroshi Nakagawa
Neurocomputing 121, 523 (2013)

2. Main Results
Diff. of log-likelihood
Better
We considered the efficiency of quantum annealing method for
Dirichlet process mixture models. In this study, Monte Carlo
simulation was performed.
21300
Wikivote
21200
21100
21000
2.5
3
3.5
4
4.5
5
0
- We constructed a method to apply quantum annealing to network
clustering.
- Quantum annealing succeeded to obtain a better solution than
conventional methods.
- The number of classes can be changed.
(cf. K. Kurihara et al. and I. Sato et al., UAI2009)
K. Kurihara et al., I. Sato et al., Proceedings of UAI2009.

3. Background
Optimization problem
To find the state (best solution) where the real-valued cost
function is minimized.
If the size of problem is small, we can easily obtain the best solution
by brute-force calculation.
However...
if the size of problem is large, we cannot obtain the best solution by
brute-force calculation in practice.
We should develop methods to obtain the best solution (at least,
better solution) efficiently.

4. Background
Cost function of most optimization problems can be represented by
Hamiltonian of classical discrete spin systems.
We can use the knowledge of statistical physics.
To find the state where the
cost function is minimized.
To find the ground state of
the Hamiltonian.
Simulated annealing (SA)
By decreasing the temperature (thermal fluctuation) gradually,
the ground state of the Hamiltonian is obtained.
S. Kirkpatrick, C. D. Gelatte, and M. P. Vecchi, Science, 220, 671 (1983).
SA can be adopted to both stochastic methods such as Monte Carlo
method and deterministic method.

5. Background
Quantum annealing (QA)
By decreasing the quantum fluctuation gradually, the ground
state of the Hamiltonian is obtained.
T. Kadowaki and H. Nishimori, Phys. Rev. E, 58, 5355 (1998).
E. Farhi, J. Goldstone, S. Gutmann, J. Lapan, A. Lundgren, and D. Preda, Science, 292, 472 (2001).
G. E. Santoro, R. Martonak, E. Tosatti, and R. Car, Science, 295, 2427 (2002).
Review articles
G. E. Santoro and E. Tosatti, J. Phys. A: Math. Gen., 39, R393 (2006).
A. Das and B. K. Chakrabarti, Rev. Mod. Phys., 80, 1061 (2008).
S. Tanaka and R. Tamura, Kinki University Series on Quantum Computing Series "Lectures on Quantum
Computing, Thermodynamics and Statistical Physics" (2012).
QA is better than SA?

6. What is CRP?

7. Chinese Restaurant Process (CRP)
Table (data class)
Restaurant (entire set)
1
1
2
3
2
4
5
3
Customer (data point)
Chinese Restaurant Process (CRP) assigns a probability for the
seating arrangement of the customers.

8. Chinese Restaurant Process (CRP)
Seating arrangement of the customers: Z =
customer i sits at the k-th table: zi = k
N
{zi }i=1
N: the number of customers
When customer i enters a restaurant with K occupied tables at
which other customers are already seated, customer i sits at a table
with the following probability:
(k-th occupied table)
+N 1
p(zi |Zzi ; )
Nk
+N 1
(new unoccupied table)
Nk: the number of customers sitting at the k-th table
: hyper parameter of the CRP
The log-likelihood of Z is given by p(Z) =
K(Z)
K(Z)
N
=1 (N
+ )
(Nk
k=1
1)!

9. What is QACRP?

10. Quantum annealing for CRP (QACRP)
QACRP uses multiple restaurants (m restaurants).
customer i sits at the k-th table in the j-th restaurant: zj,i = k
Seating arrangement of the customers in the j-th restaurant: Zj = {zj,i }
In the j-th restaurant, when customer i enters a restaurant with K
occupied tables at which other customers are already seated,
customer i sits at a table with the following probability:
Nj,k
+N 1
/m
(k-th occupied table)
m
pQA (zj,i | {Zd }d=1 {zj,i } ; , )
e
(cj,k (i)+c+ (i))f ( , )
j,k
/m
+N 1
: inverse temperature (thermal fluctuation)
: quantum fluctuation
(new unoccupied table)

11. Quantum annealing for CRP (QACRP)
/m
Nj,k
+N 1
e
(cj,k (i)+c+ (i))f ( , )
j,k
(k-th occupied table)
m
pQA (zj,i | {Zd }d=1 {zj,i } ; , )
/m
(new unoccupied table)
+N 1
c± (i) : the number of customers who sit at the k-th table in the j-th
j,k
restaurant and share tables with customer i in the (j ± 1)-th
restaurant.
j-1-th CRP
1
1
2
j+1-th CRP
j-th CRP
3
2
4
5
3
1
1
4
3
2
5
3
2
1
3
4
1
2
5
2
The above fact will be proven in the following.
3

12. Quantum annealing for CRP (QACRP)
Bit matrix representation for CRP
A bit matrix B : adjacency matrix of customers
1
1
2
3
1
2
4
3
5
4
5
B
Seating conditions ˜
2
3
4
5
1
1
0
1
0
1
1
0
1
0
0
0
1
0
1
1
1
0
1
0
0
0
1
0
1
=
N
i=1
N
n=1
˜i,n
Bi,n = Bn,i
Bi,i = 1 (i = 1, 2, · · · , N )
i, , Bi /|Bi | · B /|B | = 1 or 0
Sitting arrangement
can be represented by
the Ising model with
constraints.

13. Quantum annealing for CRP (QACRP)
Bit matrix representation for CRP
1
1
2
4
3
2
2
1
2 1 1 0 1 0
0
customers who share a
1
0 table with customer 2.
1
4
3
3
4
5
5
1
1
1 1 0 1 0
0
1
0
0
0 1 1 0 1
1
0
1
0
0 1 0 0 0
0
0
0
a set of the states that customer 2 can take
under the seating conditions.
3
4
5
1
1
0
1
0
1
1
0
1
0
0
0
1
0
1
1
1
0
1
0
0
0
1
0
1
1
1
5
2
2
3
4
5
1
0 1 0
0
1
0
1 0 1
0 1 0
1 0 1
2
3
4
5

14. Quantum annealing for CRP (QACRP)
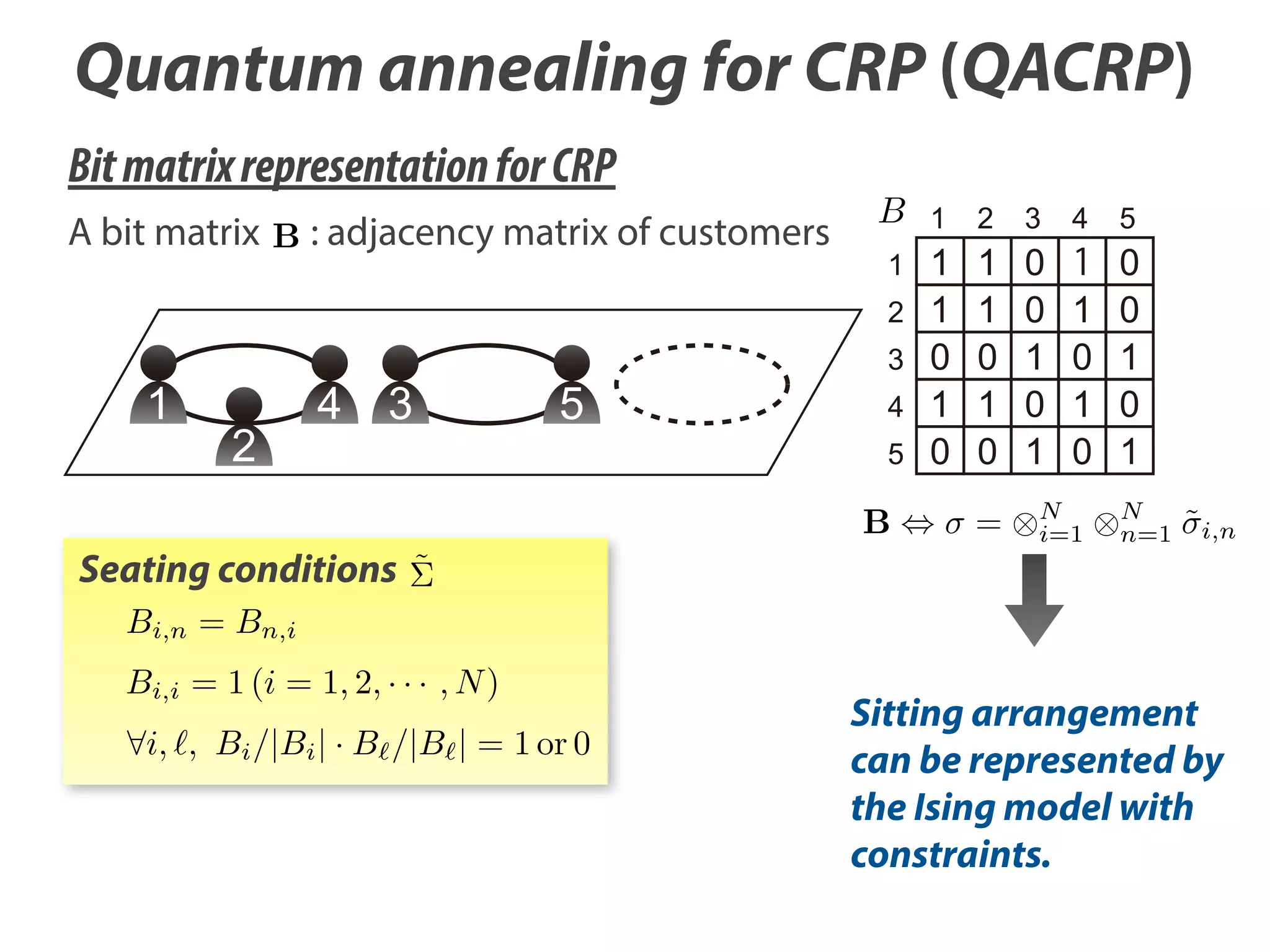
Density matrix representation for “classical” CRP
Hc = diag[E(
E(
( )
)=
p( ) =
(1)
), E(
ln p(
( )
(2)
)
+
T
e
), · · · E(
( )
T e Hc
=:
T
)
)]
˜
( )
Hc
(2
N2
˜
e Hc
Zc
Sitting arrangement can be represented by the
Ising model with constraints.

15. Quantum annealing for CRP (QACRP)
Formulation for quantum CRP
H = Hc + Hq
Hc : classical CRP
Hq : quantum fluctuation
T
pQA ( ; , ) =
Classical CRP
p(˜i | ˜i ) =
p(zi |Zzi ; )
e
(Hc +Hq )
Te
T
˜i
e
(Hc +Hq )
Hc
T e Hc
Nk
+N 1
(k-th occupied table)
+N 1
(new unoccupied table)

16. Quantum annealing for CRP (QACRP)
Formulation for quantum CRP
H = Hc + Hq
Hc : classical CRP
Hq : quantum fluctuation
T
pQA ( ; , ) =
e
(Hc +Hq )
Te
Quantum CRP
(Hc +Hq )
T
pQA (˜i | ˜i ; , ) =
˜i
e
(Hc +Hq )
Te
(Hc +Hq )
Transverse field as a quantum fluctuation
N
Hq =
N
x
i,n ,
i=1 n=1
E=
1
0
0
1
,
x
=
0 1
1 0

17. Quantum annealing for CRP (QACRP)
Approximation inference for QACRP
T
pQA ( ; , ) =
e
(Hc +Hq )
Te
=
(Hc +Hq )
pQA
j (j
ST (
,
2)
2, · · ·
m
pQA
ST ( 1 ,
2, · · ·
,
m;
, )=
N
j+1 )
e
,
E(
j=1
f ( , ) = 2 ln coth
s( j ,
By the Suzuki-Trotter decomposition,
pQA can be approximately expressed
by the classical CRP.
m;
, )+O
ef ( , )s(
Z( , )
j )/m
m
N
(˜j,i,n , ˜j+1,i,n )
=
i=1 n=1
2N
Z( , ) = sinh
m
e
E( )
m
2
m
j , j+1 )

18. Experiments
Network model & dataset
Citeseer
citation network dataset for 2110
papers.
527
I. Sato et al. / Neurocomputing 121 (2013) 523–531
. (a) Social network (assortive network), (b) election network (disassortative network) and (c) citation network (mixture of assortative
ning CRPs in which sj ðj ¼ 1; …; mÞ
ment of the j-th CRP and represents
~
espond Bj;i;n ¼ 1 to s j;i;n ¼ ð1; 0Þ⊤ and
means that we can represent Bj as
the following121 (2013) 523–531
eurocomputing theorem:
(10) is approximated by the Suzuki–
!
β2
…; sm ; β; ΓÞ þ O
;
m
1
e−β=mEðsj Þ ef ðβ;ΓÞsðsj ;sjþ1 Þ ;
¼ 1 Zðβ; ΓÞ
ð15Þ
m
∏
ð16Þ
Netscience
coauthorship network of
regarded as a similarity function between the j-th and (j+1)-th bit
matrices. If they are the same matrices, then sðs ; s Þ ¼ N . In
scientists working on a network
Eq. (2), log p ðs Þ corresponds to log e
=Z and the regularizer
term f Á Rðs ; …; s Þ is log ∏
e
¼ f ðβ;
sðs ; s Þ.
thatΓÞ∑ inference for scientists.
has 1589
Note that we aim at deriving the approximation
SA
1
−β=mEðsj Þ
j
m
m
f ðβ;ΓÞsðsj ;sjþ1 Þ
j¼1
527
j
2
jþ1
m
j¼1
j
jþ1
pQA ðs i jss i ; β; ΓÞ in Eq. (13). Using Theorem 3.1, we can derive
~
~
Eq. (4) as the approximation inference. The details of the derivation are provided in Appendix B.
Wikivote
a bipertite network constructed
4. Experiments
using QA to a DPM
We evaluated QA in a real application. We applied administrator elections.
model for clustering vertices in a network where a seating
7115 Wikipedia users.
arrangement of the CRP indicates a network partition.
ples of network structures. (a) Social network (assortive network), (b) election network (disassortative network) and (c) citation network (mixture of assortative

19. Experiments
Annealing schedule
m : Trotter number, the number of replicas; m = 16
We tested several schedules of inverse temperature.
ln(1 + t)
0 t
0t
0
=
0
= 0.2m, 0.4m, 0.6m
t : t-th iteration.
= 0.4m t is a better schedule in SA (MAP estimation).
T
= 0
m
t
is a schedule of quantum fluctuation.
T : Total number of iterations

20. Diff. of log-likelihood
Better
Results
21300
Wikivote
21200
21100
21000
2.5
3
3.5
4
4.5
0
Lmax : the maximum log-likelihood of the beam search
Beam
Lmax : the maximum log-likelihood of 16 CRPs in SA
16SAs
5

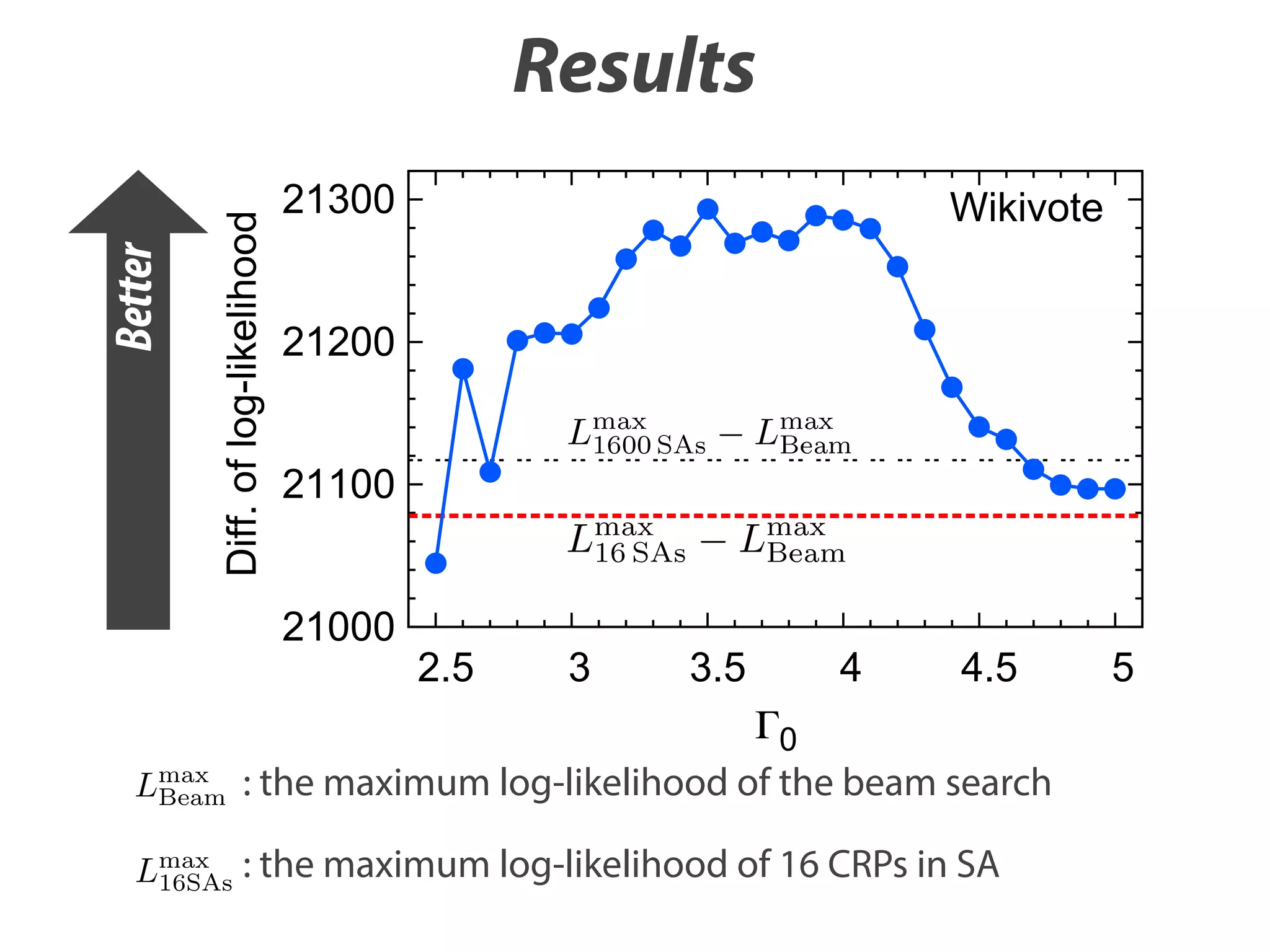
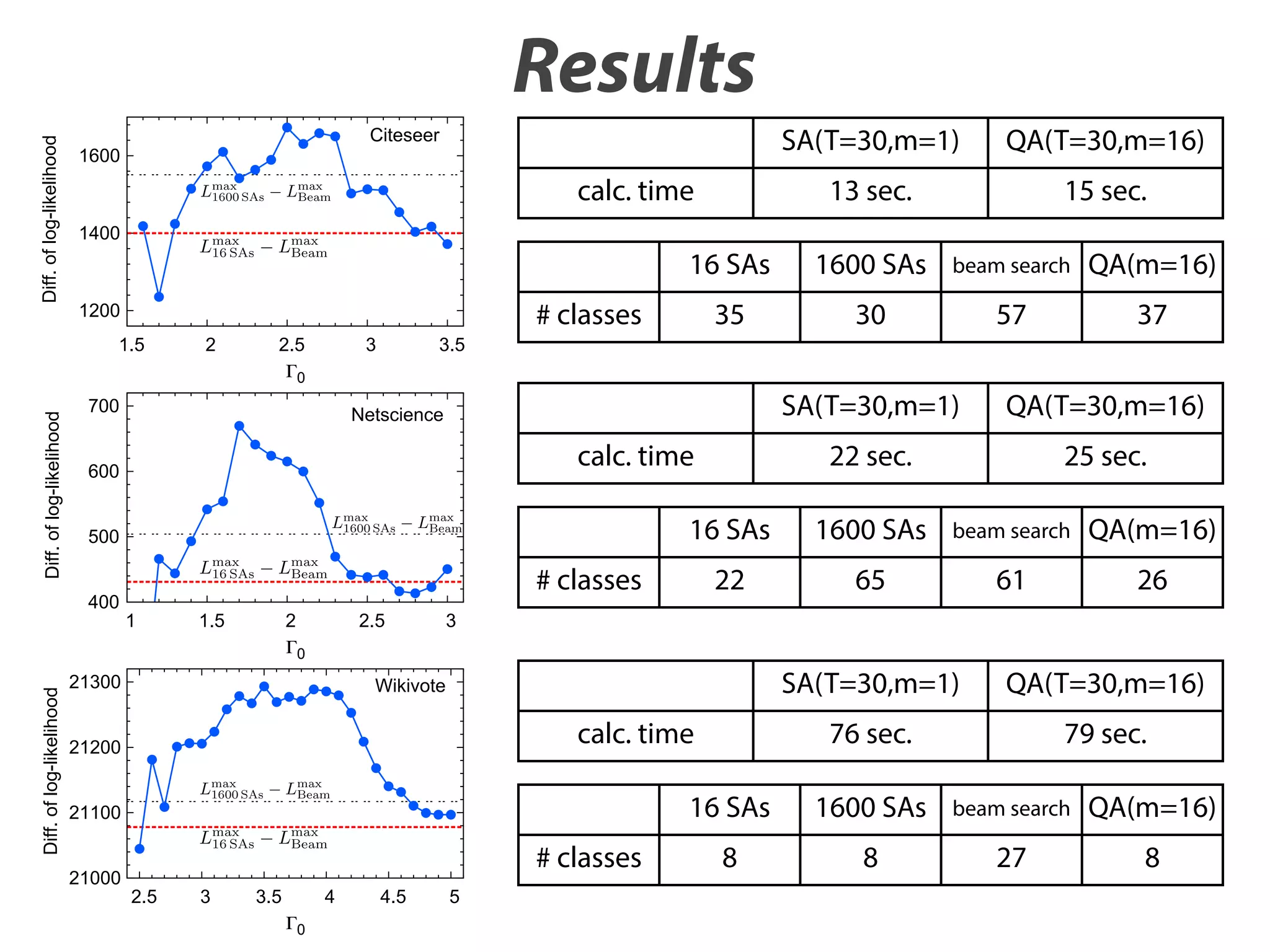
21. Diff. of log-likelihood
Results
Citeseer
1600
1400
1200
Diff. of log-likelihood
1.5
2.5
3
Netscience
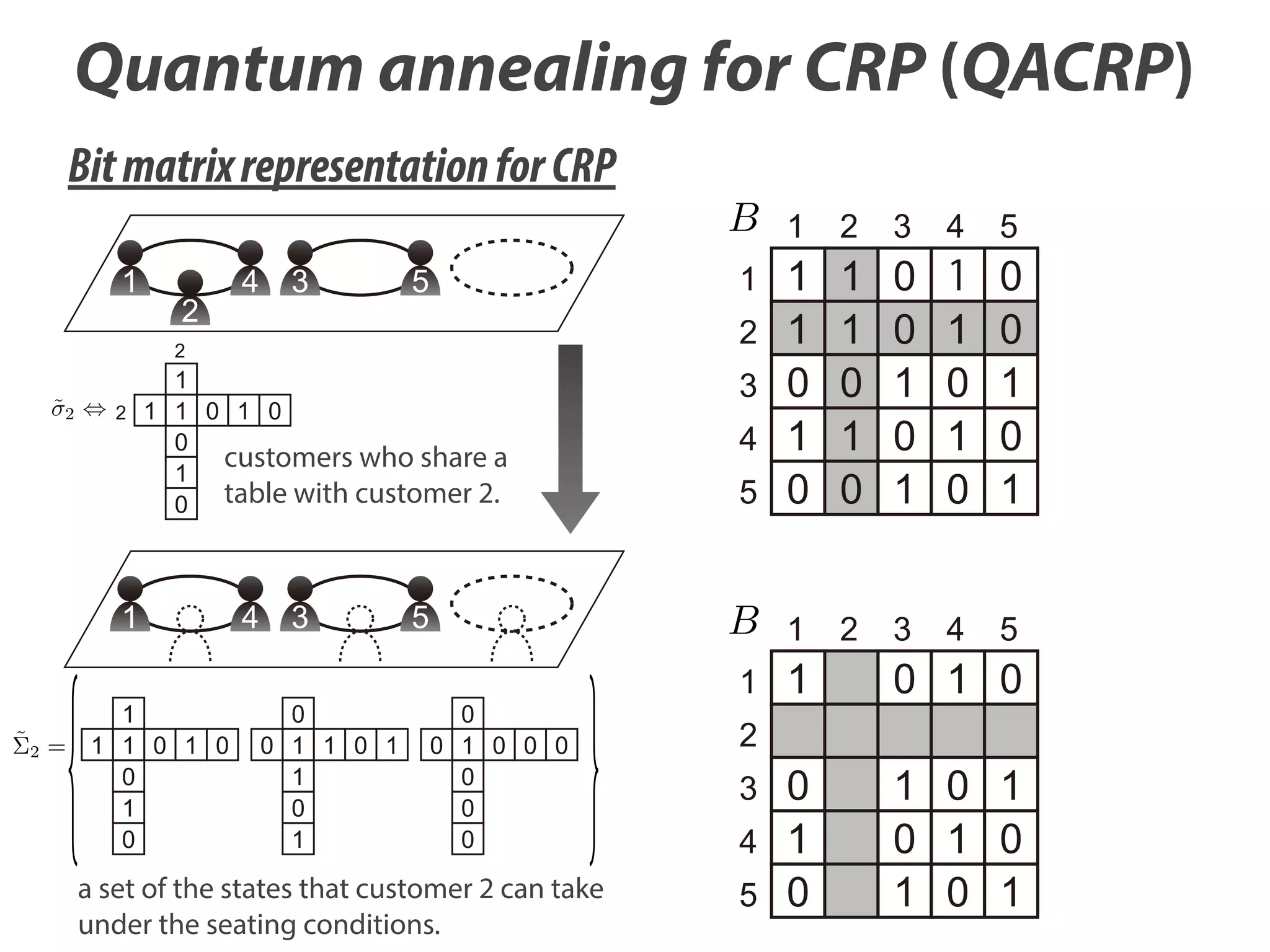
We consider multiple running CRPs in which sj ðj ¼ 1; …; mÞ
indicates the seating arrangement of the j-th CRP and represents
~
the j-th bit matrix Bj . We correspond Bj;i;n ¼ 1 to s j;i;n ¼ ð1; 0Þ⊤ and
⊤
Bj;i;n ¼ 0 to s j;i;n ¼ ð0; 1Þ , which means that we can represent Bj as
~
sj by using Eq. (5). We derive the following theorem:
600
500
1
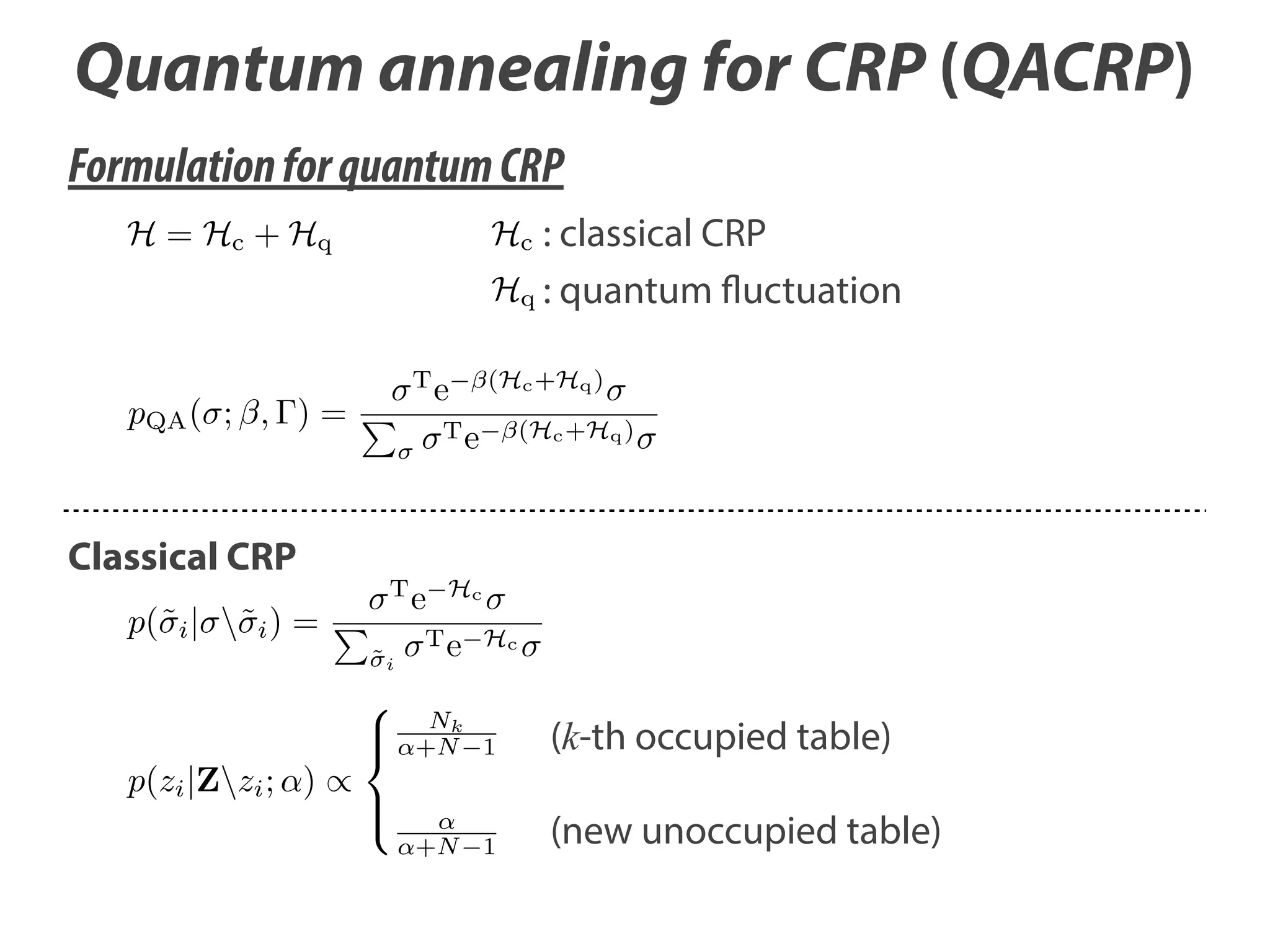
Theorem 3.1. Sato ðs;al. ΓÞ in Eq. (10) is approximated by the Suzuki–
I. pQA et β; / Neurocomputing 121 (2013) 523–531
Trotter expansion as2.5
follows: 3
1.5
2
0
pQA ðs; β; ΓÞ ¼
21300
1 ⊤ −βðHc þHq Þ
s e
s
Z
Wikivote
¼ ∑ pQA−ST ðs; s2 ; …; sm ; β; ΓÞ þ O
sj ðj≥2Þ
21200
2
!
β
;
m
pQA−ST ðs1 ; s2 ; …; sm ; β; ΓÞ
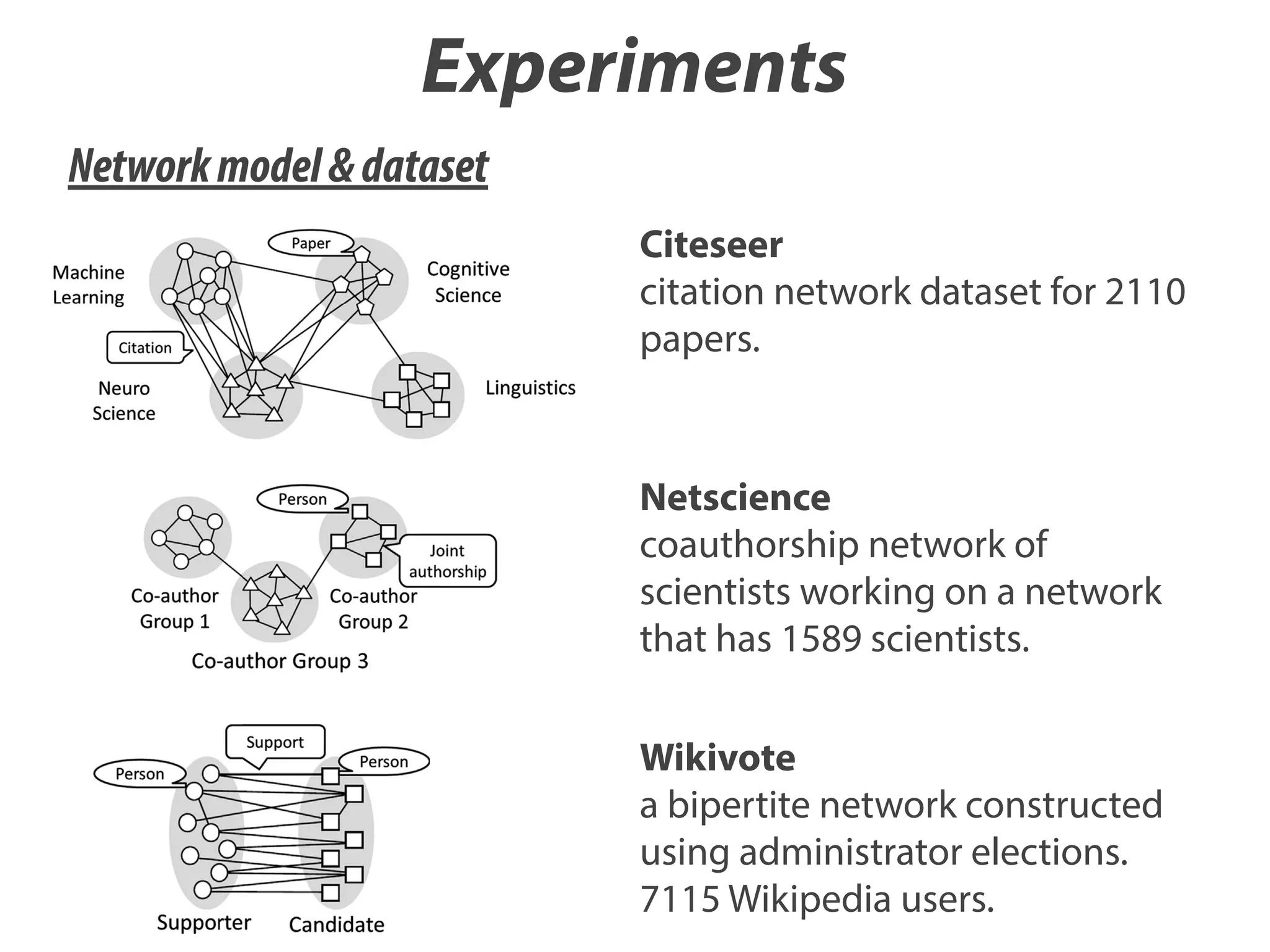
4. Experiments
ð16Þ
We evaluated QA in a real application. We applied QA to a DP
model for clustering vertices in a network where a seati
arrangement of the CRP indicates a network partition.
2.5
1
e−β=mEðsj Þ ef ðβ;ΓÞsðsj ;sjþ1 Þ ;
Zðβ; ΓÞ
j¼1
m
¼ ∏
regarded as a similarity function between the j-th and (j+1)-th
matrices. If they are the same matrices, then sðsj ; sjþ1 Þ ¼ N 2 .
Eq. (2), log pSA ðsj Þ corresponds to log e−β=mEðsj Þ =Z and the regulari
term f Á Rðs1 ; …; sm Þ is log ∏m 1 ef ðβ;ΓÞsðsj ;sjþ1 Þ ¼ f ðβ; ΓÞ∑m 1 sðsj ; sjþ
j¼
j¼
Note that we aim at deriving the approximation inference
pQA ðs i jss i ; β; ΓÞ in Eq. (13). Using Theorem 3.1, we can der
~
~
527
Eq. (4) as the approximation inference. The details of the deriv
tion are provided in Appendix B.
ð15Þ
where we rewrite s as s1 , and
21100
21000
I. Sato et al. / Neurocomputing 121 (2013) 523–531
3.5
Fig. 5. Examples of network structures. (a) Social network (assortive network), (b) election network (disassortative network) and (c) citation network (mixture of assorta
and disassortative network).
0
700
400
Diff. of log-likelihood
2
Better solution
can be obtained
by QA.
β
Γ ;
ð17Þ
f ðβ; ΓÞ ¼ 2 Fig. 5. Examples of network structures. (a) Social network (assortive network), (b) election network (disassortative network) and (c) citation netwo
log coth
m
4.1. Network model
and disassortative network).
3
3.5
4
N
4.5
5
N
~
~
sðsj ; sjþ1 Þ ¼ 0∑ ∑ δðs j;i;n ; s jþ1;i;n Þ;
ð18Þ
We used the Newman model [17] for network modeling in t

22. Diff. of log-likelihood
Results
Citeseer
1600
SA(T=30,m=1)
13 sec.
calc. time
QA(T=30,m=16)
15 sec.
1400
16 SAs
1200
1600 SAs
beam search
QA(m=16)
35
30
57
37
# classes
1.5
2
2.5
3
3.5
Diff. of log-likelihood
0
700
SA(T=30,m=1)
calc. time
600
25 sec.
16 SAs
500
400
QA(T=30,m=16)
22 sec.
Netscience
1600 SAs
beam search
QA(m=16)
22
65
61
26
# classes
1
1.5
2
2.5
3
Diff. of log-likelihood
0
21300
SA(T=30,m=1)
calc. time
21200
79 sec.
16 SAs
21100
21000
QA(T=30,m=16)
76 sec.
Wikivote
# classes
2.5
3
3.5
4
0
4.5
5
1600 SAs
beam search
QA(m=16)
8
8
27
8

23. Main Results
Diff. of log-likelihood
Better
We considered the efficiency of quantum annealing method for
Dirichlet process mixture models. In this study, Monte Carlo
simulation was performed.
21300
Wikivote
21200
21100
21000
2.5
3
3.5
4
4.5
5
0
- We constructed a method to apply quantum annealing to network
clustering.
- Quantum annealing succeeded to obtain a better solution than
conventional methods.
- The number of classes can be changed.
(cf. K. Kurihara et al. and I. Sato et al., UAI2009)
K. Kurihara et al., I. Sato et al., Proceedings of UAI2009.

24. Thank you !
Issei Sato, Shu Tanaka, Kenichi Kurihara,
Seiji Miyashita, and Hiroshi Nakagawa
Neurocomputing 121, 523 (2013)