Eligheor2
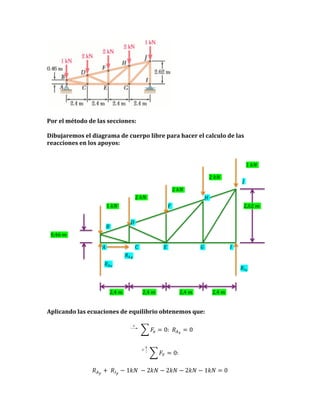
- 1. Por el método de las secciones: Dibujaremos el diagrama de cuerpo libre para hacer el calculo de las reacciones en los apoyos: 1!!"! 2!!"! !! 2!!"! 2!!"! !! 1!!"! !! 2,62!!! !! !! 0,46!!! COSMOS: Complete Online Solutions Manual Organization System COSMOS: Complete Online Solutions Manual Organization System !! !! !! !! !! !!! Chapter 4, Solution 19. 19. Chapter 4, Solution !!! !!! Free-Body Diagram: Free-Body Diagram: (a) (a) From free-body diagram of lever BCD free-body diagram of lever BCD2,4!!! 2,4!!! From 2,4!!! 2,4!!! ΣM C M C0:= 0:AB T50 (mmmm ) − 200 75(mmmm )0= 0 T ( AB 50 ) − 200 N ( N 75 ) = Σ= Aplicando las ecuaciones de equilibrio obtenemos que: (b) (b) From free-body diagramlever BCD From free-body diagram of of lever BCD ∴ TABTAB 300 ∴ = = 300 ΣFx Σ𝐹 x0:= 0: 𝑅N += + + x0.6 ( 300300 N )0= 0 = = 0: 200 N 0 C + 0.6 ( N ) = 200 Cx F ! ! ! ∴ C x = x−380380 N or or C x C x 380380 N = = N ∴C = −N ΣFy Σ= y0:= 0: y + y + (0.8 ( 300 N )0= 0 C C 0.8 300 N ) = F 𝐹! = 0: ∴ C y = −240240 N or or C y C y240240 N = = N ∴ Cy = − N 𝑅!! + Then− 1𝑘𝑁 C = C 2− 2𝑘𝑁 2 (2𝑘𝑁 2− 1𝑘𝑁 )= =2 449.44 N 𝑅!! − 2𝑘𝑁 + 2 2 = − 380 ) + 2( 240 2 0 C Then and and C = x Cx + C y = y ⎛ Cy ⎞ C Cx ⎠ x ⎝ ⎝C ⎠ ( 380 ) + ( 240 ) = 449.44 N ⎛ − 240 ⎞ ⎝ − 380380 ⎠ ⎝− ⎠ ⎞ tan 1 ⎜ ⎜⎟ y ⎟ = 1 ⎜ ⎜ ⎟ = ⎞ = 32. ° θ = θ =−tan −1 ⎛⎟ = tan −tan −1 ⎛ − 240 32.276276° ⎟ ⎜ ⎜ ⎟ or C = 449449 N 32.3° ▹ ▹ or C = N 32.3°
- 2. 𝑅!! + 𝑅!! = 8 𝑘𝑁 2,16!!! 2,62!!! ! 0,46!!! 9,6!!! Con los datos del dibujo podemos sacar: 2,16 𝛼 = tan!! = 12,68° 9,6
- 3. Si se conoce la inclinación de la armadura, podemos encontrar la medida que poseen verticalmente los elementos DC, FE y HG !! !! !! !! !! !! !! !! !! !! !! !! !! 𝐷𝐶 = 𝑦! + 𝐴𝐵 𝐹𝐸 = 𝑦! + 𝐴𝐵 𝐻𝐺 = 𝑦! + 𝐴𝐵 Donde tenemos: 𝑦! = 𝐴𝐶 tan 𝛼 , 𝑦! = 𝐴𝐸 tan 𝛼 , 𝑦! = 𝐴𝐺 tan 𝛼 𝐴 𝐶 = 2,4 𝑚 , 𝐴 𝐸 = 4,8 𝑚 , 𝐴 𝐺 = 7,2 𝑚 𝐴 𝐵 = 0,46 𝑚 , 𝛼 = 12,68° Por lo tanto 𝐷𝐶 = 𝑦! + 𝐴𝐵 = 2,4 tan 12,68 + 0,46 = 1 𝑚 𝐹𝐸 = 𝑦! + 𝐴𝐵 = 4,8 tan 12,68 + 0,46 = 1,54 𝑚 𝐻𝐺 = 𝑦! + 𝐴𝐵 = 7,2 tan 12,68 + 0,46 = 2,08 𝑚
- 4. COSMOS: Complete Online Solutions Manual Organization System Chapter 4, Solution 19. Free-Body Diagram: cuaciones de equilibrio obtenemos que: Aplicando las e (a) From free-body diagram of lever BCD ΣM C = 0: TAB ( 50 mm ) − 200 N ( 75 mm ) = 0 𝑀! = 0: ∴ TAB = 300 (b) From free-body diagram of lever BCD −2,4 2 − 4,8 2 − 7,2 Fx = 0: 200 N+ 9,6(𝑅0.6 ( 300 N ) = 0 Σ 2 − 9,6 1 + Cx + !! ) = 0 ∴ C x = −380 N or C x = 380 N 2,4 2 + 4,8 2ΣFy 7,2 2 C++9,6 (1 N ) = 0 + = 0: y 0.8 300 𝑅!! = = 4 𝑘𝑁 9,6 ∴ C y = −240 N or C y = 240 N Luego tenemos que: C = Then 2 2 Cx + C y = ( 380 )2 + ( 240 )2 = 449.44 N ⎞ 𝑅!! = 8𝑘𝑁 − 𝑅!!θ = tan −1 ⎛ −y 4𝑘𝑁 =1 ⎛ − 240 ⎞ = 32.276° 4 𝑘𝑁 ⎟ ⎟ = tan − ⎜ ⎜ and = 8 𝑘𝑁 C ⎜C ⎟ ⎝ x⎠ − 380 ⎠ ⎝ or C = ual, Calcularemos el valor de cada componente de las reacciones, por lo c449 Nse 32.3° ▹ seccionará la armadura en los elementos CE, DE y DF !! 2!!"! !!" !! 1!!"! ! !! !! !! !!" !! !!" 4!!"! 2,4!!! 2,4!!! 2,4 𝛽 = tan!! Beer, = Russell Johnston, Jr., 67,38° Vector Mechanics for Engineers: Statics and Dynamics, 8/e, Ferdinand P.1 E. Elliot R. Eisenberg, William E. Clausen, David Mazurek, Phillip J. Cornwell © 2007 The McGraw-Hill Companies.
- 5. COSMOS: Complete Online Solutions Manual Organization System Chapter 4, Solution 19. Free-Body Diagram:ecuaciones de equilibrio obtenemos que: Aplicando las (a) From free-body diagram of lever BCD ΣM C = 0: TAB ( 50 mm ) − 200 N ( 75 mm ) = 0 𝑀! = 0: ∴ TAB = 300 (b) From free-body diagram of lever BCD COSMOS: Complete Online Solutions Manual Organization System 1 𝐹!" − 2,4 4𝑘𝑁 =+ 2,4 1𝑘𝑁 ΣFx 0: 200 N + C= + 0.6 ( 300 N ) = 0 x 0 ∴ C x = −380 N or C x = 380 N Chapter 4, Solution 19. ΣFy = 0: C y + 0.8 ( 300 N ) = 0 2,4 4𝑘𝑁 − 2,4 1𝑘𝑁 𝐹!" = = 7,2 𝑘𝑁 𝑻 𝑒𝑙 𝑒𝑙𝑒𝑚𝑒𝑛𝑡𝑜 𝐶𝐸 𝑒𝑠𝑡𝑎 𝑒𝑛 𝑡𝑟𝑎𝑐𝑐𝑖ó𝑛 1 ∴ C y = −240 N or C y = 240 N Free-Body Diagram: 2 2 (a) C = C 2 + C 2 of ( 380 ) + ThenFrom free-body diagram = lever BCD ( 240 ) = 449.44 N x y ΣM C = 0: TAB ( 50 mm ) − 200 N ( 75 mm ) = 0 𝑀! = C y ⎞ ⎛ 0: ⎛ − 240 ⎞ and θ = tan −1 ⎜ ⎟ = tan −1 ⎜ ⎟ = 32.276° ∴ TAB = 300 ⎜C ⎟ ⎝ − 380 ⎠ ⎝ x⎠ (b) From free-body diagram of lever BCD or C = 449 N 32.3° ▹ −4,8 4𝑘𝑁 + 4,8 1𝑘𝑁 + 2,4 2𝑘𝑁 − 1Fcos 12,68 (𝐹!"Cx− 2,4 (sin 12,680 (𝐹!" ) = 0 Σ x = 0: 200 N + ) + 0.6 300 N ) = 𝐹!" ∴ C = −380 N or C x = 380 N x 4,8 4𝑘𝑁 − 4,8 1𝑘𝑁 − 2,4 2𝑘𝑁 = = −6,34 𝑘𝑁 Fy 0: C y + 1 cos 12,68 +Σ 2,4= sin 12,680.8 ( 300 N ) = 0 COSMOS: Complete Online Solutions Manual Organization System ∴ C y = −240 N or C y = 240 N Chapter 4, Solution 19. 2 2 2 2 ∴ 𝐹!" = 6,34 𝑘𝑁 𝑪 𝑒𝑙 𝑒𝑙𝑒𝑚𝑒𝑛𝑡𝑜 𝐷𝐹 𝑒𝑠𝑡𝑎 𝑒𝑛 𝑐𝑜𝑚𝑝𝑟𝑒𝑠𝑖ó𝑛 449.44 N C = C x + C y = ( 380 ) + ( 240 ) = Then Free-Body Diagram: ⎛ Cy ⎞ ⎛ − 240 ⎞ (a) and From free-body −diagram of lever BCD ⎟ = 32.276° θ = tan 1 ⎜ ⎟ = tan −1 ⎜ ⎟ ⎜ ⎝ 380 ⎠ ΣM C = 0:⎝ C xAB ( 50 mm )−− 200 N ( 75 mm ) = 0 T ⎠ 𝑀! = 0: or C = 449 N ∴32.3° = 300 TAB ▹ (b) From free-body diagram of lever BCD 2,4 1𝑘𝑁 − 2,4 4𝑘𝑁 + 1 634𝑘𝑁 − 1 N + 67,38 (𝐹300 N ) 0 0 ΣFx = 0: 200 sin Cx + 0.6 ( !" ) = = ∴ C = −380 N C = 380 N ∴ C y = −240 N 𝐹!" or or C y = 240 N x −2,4 1𝑘𝑁 + 2,4 4𝑘𝑁 − 1 x634𝑘𝑁 = = N) = 0 −0,93 𝑘𝑁 ΣFy = 1 sin 12,68 0: C y + 0.8 ( 300 2 2 2 2 ∴ 𝐹!" = 0,93 𝑘𝑁 𝑪 𝑒𝑙 𝑒𝑙𝑒𝑚𝑒𝑛𝑡𝑜 𝐷𝐸 𝑒𝑠𝑡𝑎 𝑒𝑛 𝑐𝑜𝑚𝑝𝑟𝑒𝑠𝑖ó𝑛 449.44 N C = C x + C y = ( 380 ) + ( 240 ) = Then and ⎛ Cy ⎞ − 240 ⎞ ⎟ = tan −1 ⎛ ⎟ = 32.276° ⎜ ⎟ ⎝ − 380 ⎠ ⎝ Cx ⎠ θ = tan −1 ⎜ ⎜ Vector Mechanics for Engineers: Statics and Dynamics, 8/e, Ferdinand P. Beer, E. Russell Johnston, Jr., Elliot R. Eisenberg, William E. Clausen, David Mazurek, Phillip J. Cornwell © 2007 The McGraw-Hill Companies. or C = 449 N 32.3° ▹