More Related Content
PPTX
Variational Template Machine for Data-to-Text Generation PPTX
Globally and Locally Consistent Image Completion PPTX
Generating Better Search Engine Text Advertisements with Deep Reinforcement L... PPTX
Towards Knowledge-Based Personalized Product Description Generation in E-comm... PPTX
Can increasing input dimensionality improve deep reinforcement learning? PDF
Trainable Calibration Measures for Neural Networks from Kernel Mean Embeddings PPTX
Statistical machine learning forecasting methods concerns and ways forward PDF
Top-K Off-Policy Correction for a REINFORCE Recommender System What's hot
PDF
FastDepth: Fast Monocular Depth Estimation on Embedded Systems PDF
東大大学院 電子情報学特論講義資料「深層学習概論と理論解析の課題」大野健太 PPTX
PDF
A PID Controller Approach for Stochastic Optimization of Deep Networks PPTX
Mutual Mean-Teaching:Pseudo Label Refinery for Unsupervised Domain Adaption o... PPTX
PredCNN: Predictive Learning with Cascade Convolutions PPTX
PDF
Depth Prediction Without the Sensors: Leveraging Structure for Unsupervised L... PDF
DeepVIO: Self-supervised Deep Learning of Monocular Visual Inertial Odometry ... PPTX
【DL輪読会】Responsive Safety in Reinforcement Learning by PID Lagrangian Methods... PPTX
MultiRec: A Multi-Relational Approach for Unique Item Recommendation in Aucti... PDF
日本ソフトウェア科学会第36回大会発表資料「帰納的プログラミングの初等教育の試み」西澤勇輝 PDF
Real-Time Semantic Stereo Matching PDF
AGenT Zero: Zero-shot Automatic Multiple-Choice Question Generation for Skill... PPTX
You Only Learn One Representation: Unified Network for Multiple Tasks PPTX
PPTX
PDF
Towards Faster and Stabilized GAN Training for High-fidelity Few-shot Image S... PPTX
Playing Atari with Six Neurons PDF
[DL輪読会]マテリアルズインフォマティクスにおける深層学習の応用 Similar to Feature engineering for predictive modeling using reinforcement learning
PPTX
Deep reinforcement learning for imbalanced classification PPTX
Mastering Atari, Go, Chess and Shogi by Planning with a Learned Model (MuZero) PDF
論文紹介-Multi-Objective Deep Reinforcement Learning PDF
PDF
Jubatusにおける大規模分散オンライン機械学習 PPTX
PDF
強化学習とは (MIJS 分科会資料 2016/10/11) PDF
レコメンドアルゴリズムの基本と周辺知識と実装方法 PDF
[Dl輪読会]introduction of reinforcement learning PDF
分散型強化学習手法の最近の動向と分散計算フレームワークRayによる実装の試み PDF
DOCX
PPTX
PPTX
PDF
SSII2021 [TS2] 深層強化学習 〜 強化学習の基礎から応用まで 〜 PPTX
Efficient Deep Reinforcement Learning with Imitative Expert Priors for Autono... PDF
PPTX
PDF
PDF
論文紹介:”Playing hard exploration games by watching YouTube“ More from harmonylab
PDF
A Study on a Generation Method for Keirin Rider Introduction Articles Using R... PDF
METAGPT: META PROGRAMMING FOR A MULTI-AGENT COLLABORATIVE FRAMEWORK PDF
【修士論文】印象タグに基づく客観的特徴を用いた反復型衣服画像生成システムに関する研究 PDF
Research on Manual Creation Support Based on Technical Writing Using Large La... PDF
Collaborative Document Simplification Using Multi-Agent Systems PDF
Can Large Language Models perform Relation-based Argument Mining? PDF
UniPAD: A Universal Pre-training Paradigm for Autonomous Driving PDF
Efficient anomaly detection in tabular cybersecurity data using large languag... PDF
APT-LLM Embedding-Based Anomaly Detection of Cyber Advanced Persistent Threat... PDF
CTINexus: Automatic Cyber Threat Intelligence Knowledge Graph Construction Us... PDF
Mixture-of-Personas Language Models for Population Simulation PDF
QuASAR: A Question-Driven Structure-Aware Approach for Table-to-Text Generation PDF
Large Language Model based Multi-Agents: A Survey of Progress and Challenges PDF
Mixture-of-Personas Language Models for Population Simulation PDF
TransitReID: Transit OD Data Collection with Occlusion-Resistant Dynamic Pass... PDF
Data Scaling Laws for End-to-End Autonomous Driving PDF
DeepSeek-R1: Incentivizing Reasoning Capability in LLMs via Reinforcement Lea... PDF
Is Ego Status All You Need for Open-Loop End-to-End Autonomous Driving? PDF
Encoding and Controlling Global Semantics for Long-form Video Question Answering PDF
AECR: Automatic attack technique intelligence extraction based on fine-tuned ... Feature engineering for predictive modeling using reinforcement learning
- 1.
Feature Engineering forPredictive
Modeling Using Reinforcement Learning
Udayan Khurana, Horst Samulowitz, Deepak Turaga
北海道大学大学院情報科学研究科
調和系工学研究室
修士1年 吉田
2018年11月2日 論文紹介ゼミ
- 2.
紹介する論文
• タイトル
– FeatureEngineering for Predictive Modeling Using Reinforcement
Learning
• 著者
– Udayan Khurana*, Horst Samulowitz*, Deepak Turaga*
– *IBM Research AI
• 学会
– AAAI2018
• 概要
– 強化学習によるFeature Engineering
– 多数のデータセットで既存手法を超える精度
1
- 3.
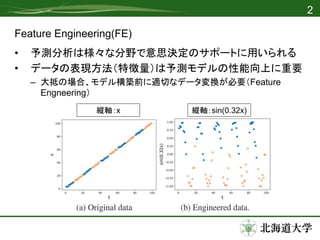
- 4.
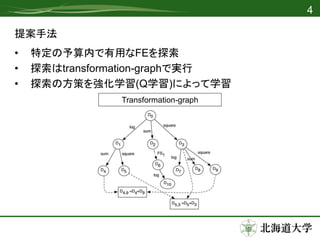
- 5.
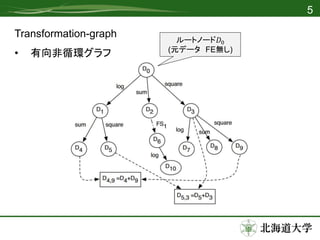
- 6.
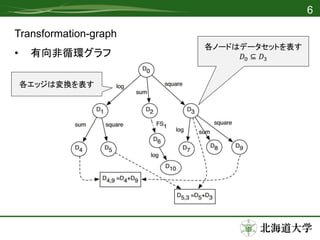
- 7.
- 8.
- 9.
- 10.
- 11.
探索アルゴリズム
• 推定報酬𝑅の設定によって探索の戦略を決定
– Q学習によって𝑅を学習
•シンプルな探索戦略は人手で作れる
– 深さ優先探索
– 幅優先探索
– Cognito (同じ著者の先行研究、実験で比較)
• Khurana, U.; Turaga, D.; Samulowitz, H.; and Parthasarathy, S. 2016b.
Cognito: Automated feature engineering for supervised learning. In
Proceedings of the IEEE 16th International Conference on Data Mining
Workshops 1304–1307.
– シンプルな探索戦略は特定の状況では適切に機能するが、
様々な状況下で機能する統一戦略を人手で行うのは困難
10
- 12.
𝑅を決定する要素
1. ノード𝑛の精度
– ノードの精度が高いほどそのノードからの探索が促進される
2.変換𝑡の𝐺𝑖までの平均即時報酬
3. 変換𝑡がルートノードからノード𝑛までに適用された回数
4. ノード𝑛とその親の精度の利得
5. ノードの深さ
– 変換シーケンスの相対的な複雑さにペナルティをかけるために使用
6. 𝐺𝑖までに使った予算の割合(𝑏 𝑟𝑎𝑡𝑖𝑜 =
𝑖
𝐵 𝑚𝑎𝑥
)
7. ノード𝑛の特徴数の元のデータセットに対する比
– どれだけ増えたか
8. 変換が特徴選択かどうか
9. データセットに数値特徴、日時特徴、文字列特徴、などが含まれているか
どうか
11
- 13.
Q-Learning with FunctionApproximation
• ステップ𝑖
– 行動(ノードに変換を適用)により新しいノード𝑛𝑖が生成される
– モデルの訓練テスト
• 精度𝐴(𝑛𝑖)となる新しいデータセットが得られる
• 各ステップでの即時報酬
– 𝑟𝑖 = max
𝑛′∈𝜃(𝐺 𝑖+1)
𝐴 𝑛′
− max
𝑛∈𝜃(𝐺 𝑖)
𝐴(𝑛)
• 𝑟0 = 0
• 状態𝑠𝑖からの累積報酬
– 𝑅 𝑠𝑖 = 𝑗=0
𝐵 𝑚𝑎𝑥
𝛾 𝑖 𝑟𝑖+𝑗
• 𝑠𝑖:グラフ𝐺𝑖と残り予算𝑏 𝑟𝑎𝑡𝑖𝑜
• 𝛾 ∈ [0,1):割引率
• 目的
– 累積報酬𝑅 𝑠𝑖 を最大にする方策Π∗
を見つける
12
- 14.
Q-Learning with FunctionApproximation
• Q学習
– 方策Πの𝑄関数
• 𝑄 𝑠, 𝑐 = 𝑟 𝑠, 𝑐 + 𝛾𝑅Π
(𝛿 𝑠, 𝑐 )
– 𝛿: 𝑆 × 𝐶 → 𝑆 仮想遷移関数
– 最適方策 Π∗(𝑠) = argmax
𝑐
|𝑄(𝑠, 𝑐)|
• 𝑆のサイズを考えると𝑄関数を直接学習することは不可能
• 線型結合による近似
– 𝑄 𝑠, 𝑐 = 𝑤 𝑐 𝑓(𝑠)
• 𝑤 𝑐:行動𝑐の重みベクトル
• 𝑓 𝑠 = 𝑓(𝑔, 𝑛, 𝑡, 𝑏)
– 状態と残りの予算比率のベクトル
13
- 15.
Q-Learning with FunctionApproximation
• Q関数の線型結合による近似
– 𝑄 𝑠, 𝑐 = 𝑤 𝑐 𝑓(𝑠)
• 𝑤 𝑐の更新ルール
– 𝑤 𝑐 𝑗 ← 𝑤 𝑐 𝑗 + 𝛼 𝑟𝑗 + 𝛾 max
𝑛′,𝑡′
𝑄 𝑔′, 𝑐′ − 𝑄 𝑔, 𝑐 𝑓(𝑔, 𝑏)
• 𝑔′:ステップ𝑗 + 1のグラフ
• 𝛼:学習率
– この証明
• Irodova, M., and Sloan, R. H. 2005. Reinforcement learning and
function approximation. In FLAIRS Conference, 455–460.
14
- 16.
- 17.
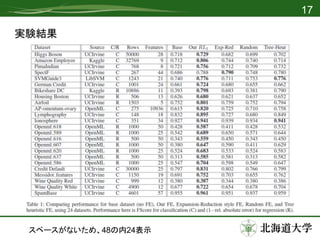
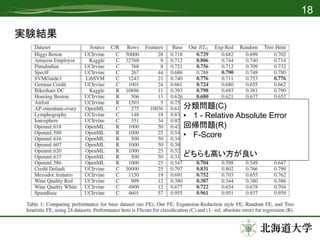
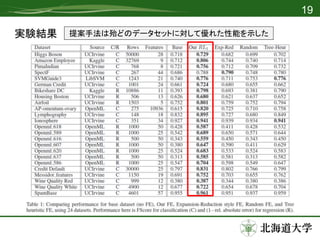
実験
• 48のデータセットに対してテスト
– 5つFEを比較
•Base dataset
– 元データ(FE無し)
• 提案手法(𝑅𝐿1)
– 𝐵 𝑚𝑎𝑥 = 100
• Expansion-reduction
– 全ての変換を別々に適用 → 特徴選択
• Random
– ランダムな特徴にランダムに変換関数を適用 ×100
• Tree-Heur
– Khurana, U.; Turaga, D.; Samulowitz, H.; and Parthasarathy, S. 2016b. Cognito: Automated feature
engineering for supervised learning. In Proceedings of the IEEE 16th International Conference on
Data Mining Workshops 1304–1307.
– 学習アルゴリズム
• Random Forestを使用
– ハイパーパラメータはBase datasetをもとに決定したものを使用
16
- 18.
- 19.
- 20.
- 21.
- 22.
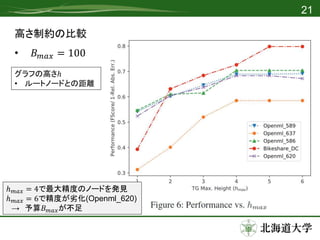
高さ制約の比較
• 𝐵 𝑚𝑎𝑥= 100
21
ℎ 𝑚𝑎𝑥 = 4で最大精度のノードを発見
ℎ 𝑚𝑎𝑥 = 6で精度が劣化(Openml_620)
→ 予算𝐵 𝑚𝑎𝑥が不足
グラフの高さℎ
• ルートノードとの距離
- 23.