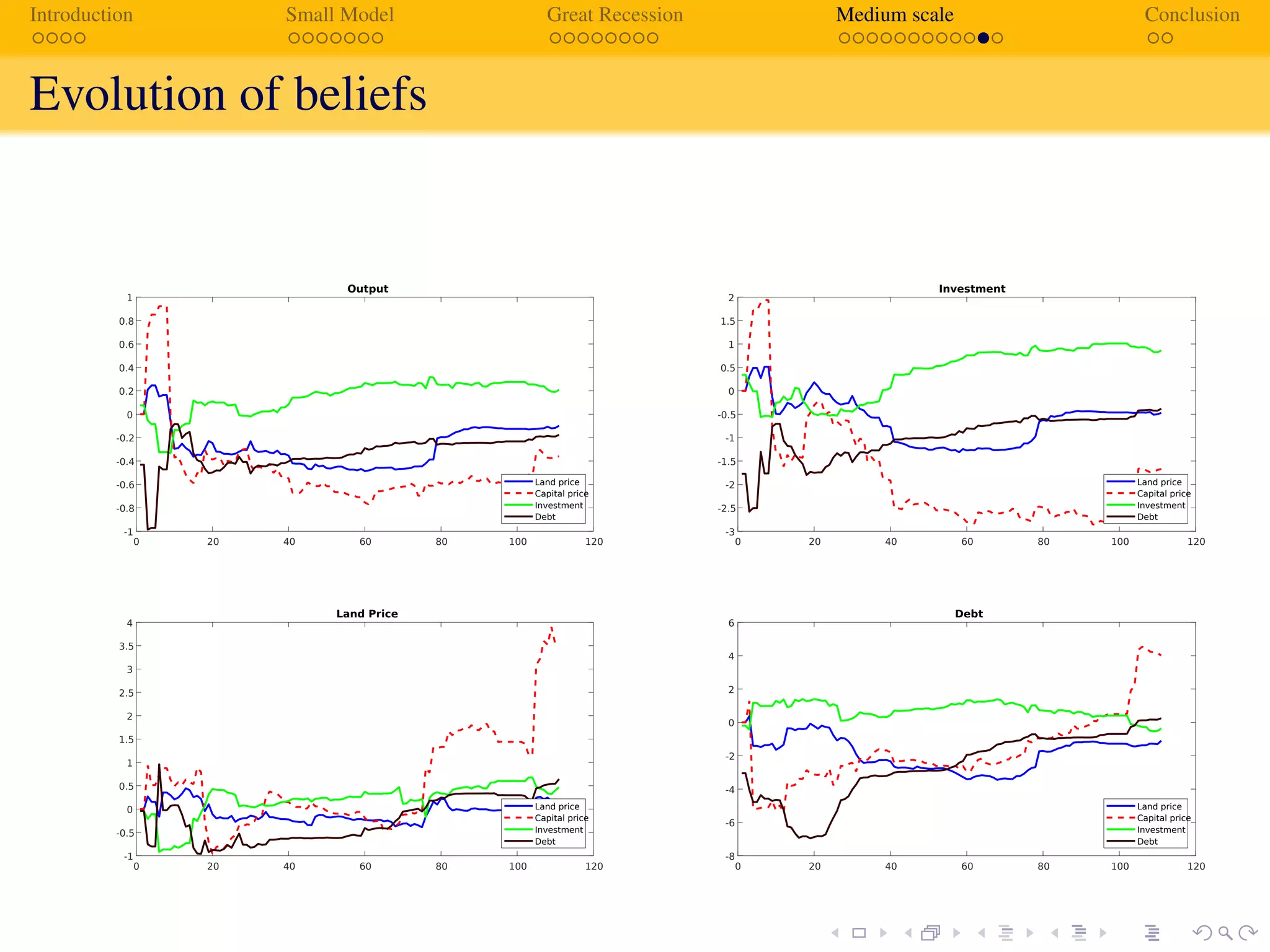
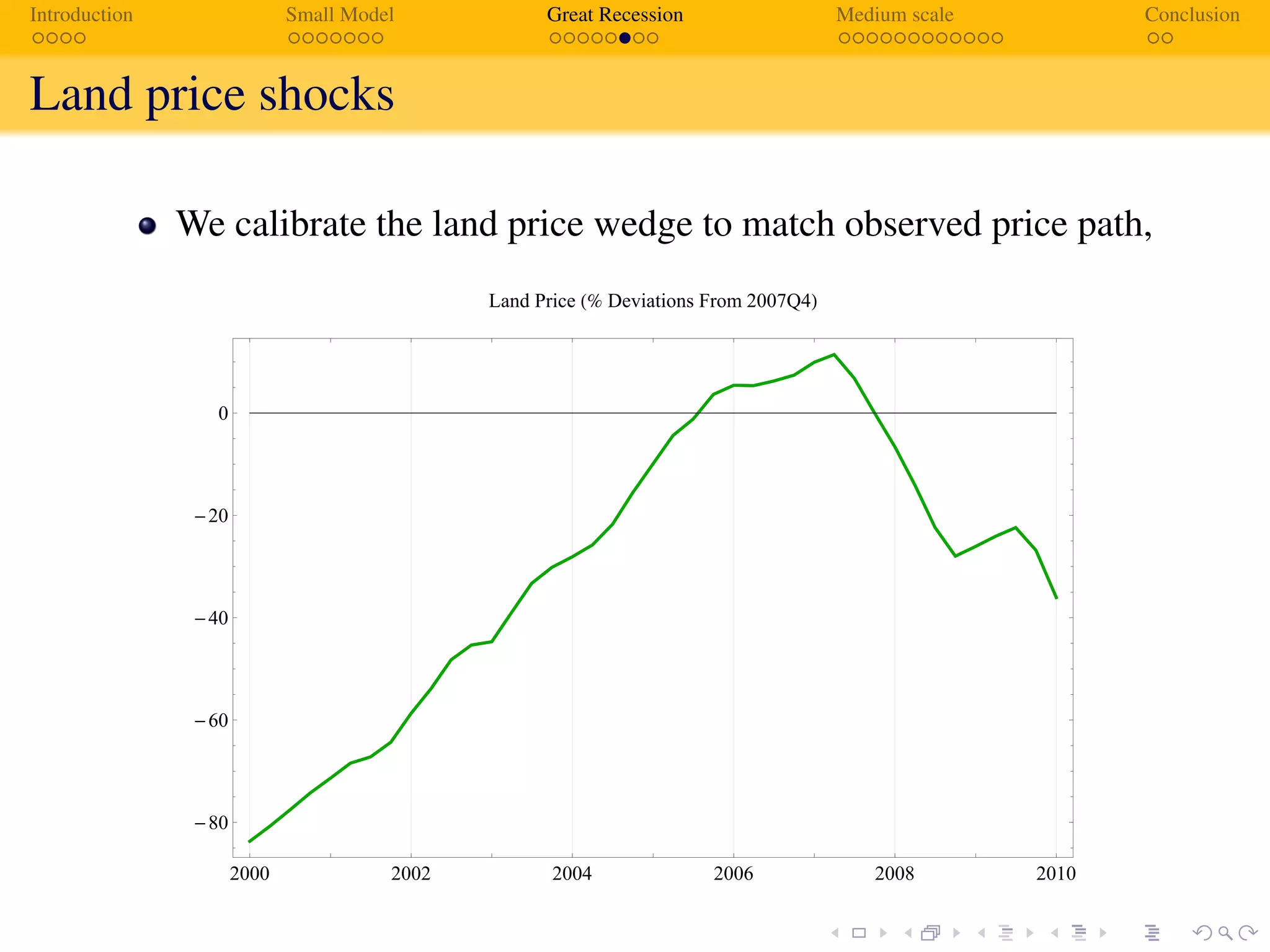
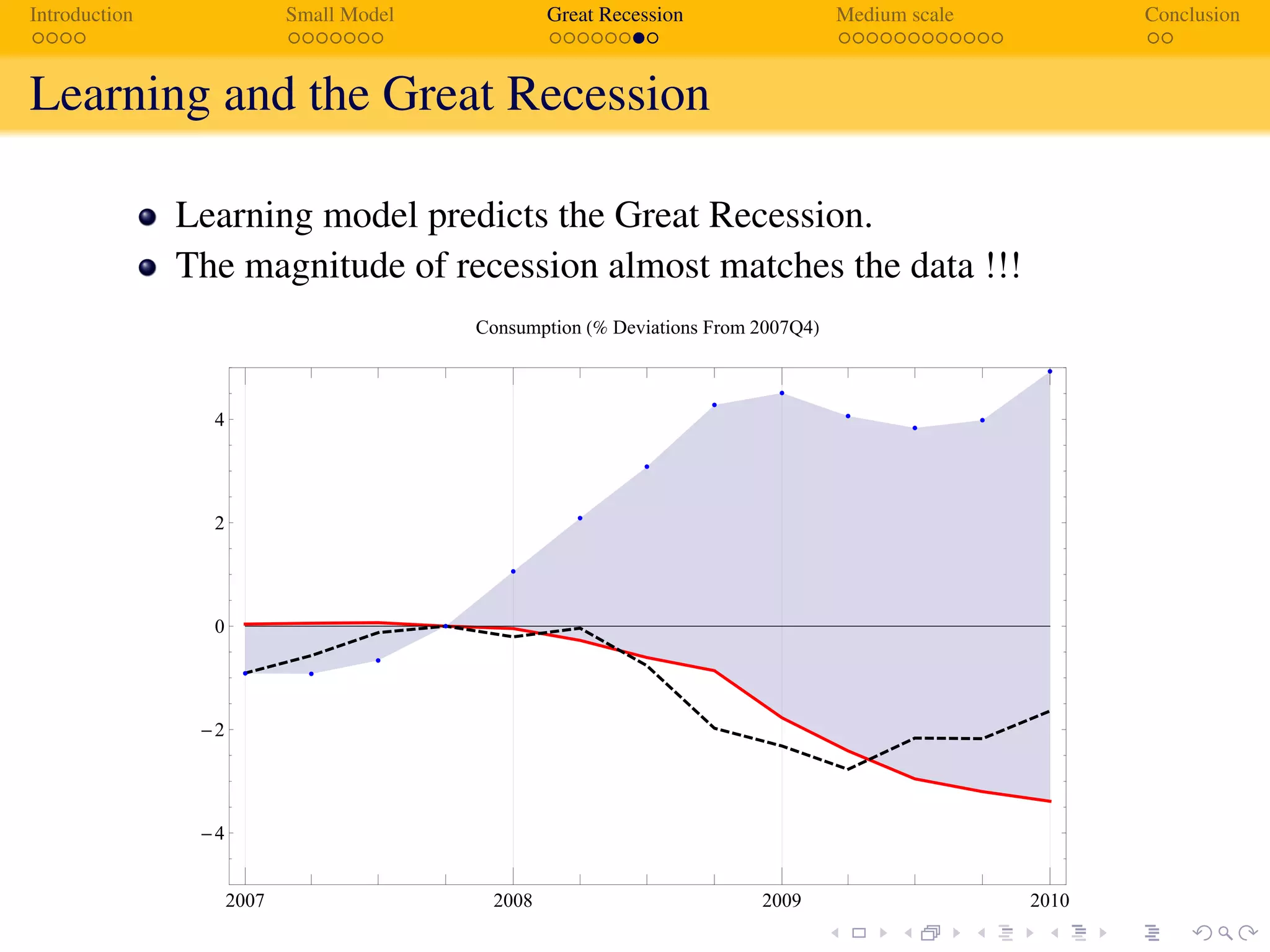
The document analyzes how adaptive learning may have contributed to the Great Recession, contrasting it with the rational expectations model. It presents a medium-scale model which demonstrates that agents' evolving perceptions of the economy can significantly influence financial behaviors and leverage, predicting a recession that aligns closely with observed data. The findings highlight time-varying impacts of shocks and the inadequacies of traditional rational expectations during financial crises.

1. Introduction Small Model Great Recession Medium scale Conclusion
Financial Frictions under Learning
Patrick A. Pintus1 Jacek Suda2 Burak Turgut3
1CNRS-InSHS and Aix-Marseille University
2NBP, SGH, and FAME|GRAPE
3Bocconi University and FAME|GRAPE
SNDE Annual Meeting
Federal Reserve Bank of Dallas, March 28, 2019

2. Introduction Small Model Great Recession Medium scale Conclusion
Financial Crisis and Expectations
2007-08 US financial crisis has reinforced interest in relaxing
rational expectations assumption.
Who had a decent approximation of crisis probability at the end
of the “Great Moderation”?
Who had a correct perception of process driving financial
shocks?
1996-2006 decade witnessed huge rise in housing prices index.
By the end of 2008 household leverage ratio rose from about 0.64
to about 1.26!
This is in stark contrasts with flat leverage during 1980-1995
period.
Assumption that agents know probability distributions rather
strong!

3. Introduction Small Model Great Recession Medium scale Conclusion
Financial Crisis and Expectations
0.7
0.8
0.9
1
1.1
1.2
1.3
1.4
US Household Leverage Ratio 1980Q1-2010Q3
0.4
0.5
0.6
1980Q1
1984Q1
1988Q1
1992Q1
1996Q1
2000Q1
2004Q1
2008Q1
1996-2006 decade witnessed huge rise in housing prices index.
By the end of 2008 household leverage ratio rose from about 0.64 to
about 1.26!
This is in stark contrasts with flat leverage during 1980-1995 period.

4. Introduction Small Model Great Recession Medium scale Conclusion
Learning Financial Shocks and the Great Recession
Our paper:
Allow agents’ perception about the structure of the economy to
evolve over time.
Examine if learning could have contributed to the Great
Recession (see Pintus and Suda (2019)
Estimate medium scale model

5. Introduction Small Model Great Recession Medium scale Conclusion
What we do
Consider RBC models with collateral constraint:
variant of Kiyotaki and Moore (1997) based on Pintus and Suda
(2019).
variant of Liu, Wang and Zha (2013)
Replace rational expectations (RE) with adaptive learning.
Calibrate/estimate the model using US data from
1996Q1-2008Q4 period.
Focus on financial shocks driving leverage:
a large temporary negative shock to leverage in 2008Q4,
Compare the responses under both RE and learning.

6. Introduction Small Model Great Recession Medium scale Conclusion
What we find
Agents gradually learn the structure of the economy.
Learning model delivers a sizeable recession in 2008-2010,
...whereas RE model predicts a counterfactual expansion.
In a medium scale model learnign still matters .

7. Introduction Small Model Great Recession Medium scale Conclusion
Representative agent
A representative agent solves:
max E∗
0
∞
t=0
βt
Ct − ψN1+χ
t
1+χ
1−σ
− 1
1 − σ
,
subject to:
budget constraint
Ct+Kt+1−(1−δ)Kt+TtQt(Lt+1−Lt)+(1+R)Bt = Bt+1+AKα
t Lγ
t N1−α−γ
t
exogenous interest rate (SOE)
E∗
t denotes expectations at time t.
Tt is a shortcut for land demand shock.

8. Introduction Small Model Great Recession Medium scale Conclusion
Borrowing constraint
Agents face borrowing constraint
˜ΘtE∗
t [Qt+1]Lt+1 ≥ (1 + R)Bt+1,
where
˜Θt ≡ Θt
E∗
t [Qt+1]
Q
ε
We allow leverage to respond to changes in the land price:
microfounded in simple moral hazard setting,
ε > 0 agrees with evidence in Mian and Sufi (2011) on US micro
data for the 2000s.

9. Introduction Small Model Great Recession Medium scale Conclusion
Leverage process
Θt is exogenous and subject to random shocks
Θt = Θ
1−ρθ
Θρθ
t−1Ξt.
Ξt: leverage shocks,
Θ: mean (steady-state) leverage level,
ρθ: persistence of impact of leverage shocks,
agents learn ρθ (and possibly Θ).
Similarly Tt is subject to random shocks
Tt = TρT
t−1Ψt

10. Introduction Small Model Great Recession Medium scale Conclusion
FOCs
Borrowers ’ first-order conditions are
Ct : Λt = Ct − ψ
N1+χ
t
1 + χ
−σ
Nt : ψNχ+α+γ
t = (1 − α − γ)AKα
t Lγ
t
Lt+1 : TtQtΛt = βE∗
t [Tt+1Qt+1Λt+1] + βγE∗
t [Λt+1Yt+1/Lt+1]
+Φt
˜ΘtE∗
t [Qt+1],
Kt+1 : Λt = βE∗
t [Λt+1(αYt+1/Kt+1 + 1 − δ)]
Bt+1 : Λt = β(1 + R)E∗
t [Λt+1] + (1 + R)Φt

11. Introduction Small Model Great Recession Medium scale Conclusion
REE
Linearized expectational system (in log levels):
Xt = AXt−1 + BE∗
t−1[Xt] + CE∗
t [Xt+1] + N + Dξt + Fψt,
Xt ≡ (ct, qt, λt, φt, bt, kt, θt, τt), ξt and ψt are innovations.
Under REE, E∗
t = Et and there exists a unique stationary
equilibrium
Xt = Mre
Xt−1 + Hre
+ Gre
ξt + Jre
ψt,
where Mre
and Hre
solve
M = [I8 − CM]
−1
[A + BM],
H = [I8 − CMre
]
−1
[BH + CH + N]

12. Introduction Small Model Great Recession Medium scale Conclusion
Learning
Relax RE assumption: E∗
t = Et.
Agents as econometricians:
Endow agents with a perception of the equilibrium law of motion
(PLM)
Xt = MXt−1 + H + Gξt + Jψt,
has the same VAR(1) structure as RE equilibrium, but
admits M = Mre
, H = Hre
, G = Gre
, J = Jre
.
Agents update their “beliefs” by estimating a VAR(1).
Agents use PLM to form expectations
Eτ Xτ+1 = Mτ−1Xτ + Hτ−1

13. Introduction Small Model Great Recession Medium scale Conclusion
Learning
Agents as econometricians:
Actual low of motion becomes
[I8 −CMt−1]Xt = [A+BMt−2]Xt−1 +[BHt−2 +CHt−1 +N]+Dξt +Fψt
Assume recursive updating of the perceived law of motion
Ωt = Ωt−1 + ν(Xt − Ωt−1Zt−1)Zt−1R−1
t
Rt = Rt−1 + ν(Zt−1Zt−1 − Rt−1),
where Zt = [1, Xt ] and Ω = [H M]
OLS/RLS if νt = 1/t,
constant gain if νt = ν.
REE: perceived and actual laws of motions coincide.

14. Introduction Small Model Great Recession Medium scale Conclusion
Experiment
Agents learn and at the onset of the recession
the associated matrix in PLM is M2008Q4.
if agents have learned/estimated ρθ, matrix M2008Q4 reflects that.
Shocks and beliefs (under learning) affects financial constraint.
Given the stochastic process, in 2008Q4 agents’ perception does
not match the true process M2008Q4 = MRE.
The actual law of motion will reflect that.

15. Introduction Small Model Great Recession Medium scale Conclusion
Set-up: calibration
Calibration:
- Model delivers average values for debt-to-GDP and land
value-to-GDP ratios for the period 1996Q1- 2008Q4:
B/Y ≈ 0.52 and QL/Y ≈ 0.59
µ β δ α γ ε ν
0.99 0.96µ 0.025 0.33 0.0093 0.5 0.004
Procyclical leverage:
- We set ε = 0.5
(calibrated from Mian and Sufi, 2011).
Gain parameter:
- Constant gain learning parameter: νt = 0.004
(regression with forgetting half-length of 40 years).

16. Introduction Small Model Great Recession Medium scale Conclusion
Set-up: estimation
Leverage process :
- We take out of the raw data on leverage the endogenous
component related to leverage land prices elasticity
- We estimate an AR(1) process on the residual (exogenous)
component
θt = (1 − ρθ)¯θ + ρθθt−1 + ξt
- RE corresponds to OLS estimates for 1975-2010 for ρθ
i.e. ρθ = 0.976, ¯Θ = 0.88
- Following the observed sequence of financial innovations
overestimation of persistence of shocks arises endogenously

17. Introduction Small Model Great Recession Medium scale Conclusion
Set-up: estimation
Leverage process :
2000 2005 2010
0.970
0.975
0.980
0.985
0.990
CG and OLS estimates of persistence of leverage

18. Introduction Small Model Great Recession Medium scale Conclusion
Shocks
Financial shocks:
- We use residuals from the estimated AR(1) process leverage
shocks, ˆξt.

19. Introduction Small Model Great Recession Medium scale Conclusion
Shocks
Financial shocks:
- We use residuals from the estimated AR(1) process leverage
shocks, ˆξt.
Estimated innovations/shocks to leverage
2000 2002 2004 2006 2008 2010
0.05
0.00
0.05
Innovations OLS and CG

20. Introduction Small Model Great Recession Medium scale Conclusion
Shocks
Financial shocks:
- We use residuals from the estimated AR(1) process leverage
shocks, ˆξt.
Agents beliefs are endogenous and driven by these shocks

21. Introduction Small Model Great Recession Medium scale Conclusion
Learning and the Great Recession
CAN LEARNING EXPLAIN THE GREAT RECESSION?

22. Introduction Small Model Great Recession Medium scale Conclusion
Land price shocks
We calibrate the land price wedge to match observed price path,
2000 2002 2004 2006 2008 2010
80
60
40
20
0
Land Price Deviations From 2007Q4

23. Introduction Small Model Great Recession Medium scale Conclusion
Learning and the Great Recession
Learning model predicts the Great Recession.
The magnitude of recession almost matches the data !!!
2007 2008 2009 2010
4
2
0
2
4
Output Response Over Time Deviations From 2007Q4

24. Introduction Small Model Great Recession Medium scale Conclusion
Learning and the Great Recession
Learning model predicts the Great Recession.
The magnitude of recession almost matches the data !!!
2007 2008 2009 2010
4
2
0
2
4
Consumption Deviations From 2007Q4

25. Introduction Small Model Great Recession Medium scale Conclusion
Learning and the Great Recession
Learning model predicts the Great Recession.
The magnitude of recession almost matches the data !!!
2007 2008 2009 2010
20
0
20
40
60
80
100
Borrowing Deviations From 2007Q4

26. Introduction Small Model Great Recession Medium scale Conclusion
Findings
Learning model predicts a boom in the early 2000s,
... as well as a sizeable recession beginning 2007Q3,
Model with rational expectations generates a fall in output up to
2007Q3
... followed by an expansion
=⇒ both at odds with the data.

27. Introduction Small Model Great Recession Medium scale Conclusion
Extending the model
Introduction
Contribution and Main Findings
• Bayesian estimation of a medium-scale DSGE model with housing and collateral
constraints for US under adaptive learning
• Better t of model to data
• Learning behaviour generates time-varying impact of shocks
• The impact of shocks are larger and more persistent during Great Recession
under AL relative to RE
• Later: What are the implications of non-rational expectations for monetary and
macroprudential policies?

28. Introduction Small Model Great Recession Medium scale Conclusion
Set-up
The Model Economy
In a Nutshell
• Two types of agents:
1 Households: Consume, purchase land, enjoy leisure and save. More patient.
2 Entrepreneurs: Consume and produce. Needs external nancing for
investment subject to borrowing constraints.
• Four types of commodities:
1 Labor
2 Goods
3 Land
4 Loanable bonds

29. Introduction Small Model Great Recession Medium scale Conclusion
Households
The Model Economy
Households
Uh
t = Et
∞
∑
t=0
βt
At log(Ch,t −γhCh,t−1)+ϕtlogLht −ψtNh,t
s.t.
Ch,t +ql,t(Lh,t −Lh,t−1)+
St
Rt
≤ wtNh,t +St−1
• Exogenous processes:
At = At−1(1+λat);lnλat = (1−ρa)ln¯λa +ρalnλat−1 +σaεa,t
lnϕt = (1−ρϕ )ln ¯ϕ +ρϕ lnϕt−1 +σϕ εϕ,t
lnψt = (1−ρψ )ln ¯ψ +ρψ lnψt−1 +σψ εψ,t

30. Introduction Small Model Great Recession Medium scale Conclusion
Entrepreneurs
The Model Economy
Entrepreneurs
Ue
t = Et
∞
∑
t=0
βt
log(Ce,t −γeCe,t−1)
s.t.
Ce,t +ql,t(Le,t −Le,t−1)+
It
Qt
+wtNe,t +Bt−1 ≤ Zt L
φ
e,t−1K
φ
t−1
α
N1−α
e,t−1 +
Bt
Rt
Kt = (1−δ)Kt−1 + 1−
Ω
2
It
It−1
− ¯λI
2
It
Bt ≤ θtEt ql,t+1Le,t +qk,t+1Kt
• Exogenous processes:
Zt = ZP
t νz,t
ZP
t = ZP
t−1λz,t;lnλz,t = (1−ρz)ln¯λz +ρzlnλzt−1 +σzεz,t
lnνz,t = ρνz lnνz,t +σνz ενz,t

31. Introduction Small Model Great Recession Medium scale Conclusion
Model dynamics
The Model Economy
Model Dynamics
• The linear model can be represented as:
A0yt−1 +A1yt +A2E∗
t yt+1 +A3ωt = const
ωt −B0ωt−1 −B1εt = 0
where yt is the vector of log-linearised model variables and ωt is the vector of
exogenous processes
• Rational Expectations Equilibrium (REE):
xt = µ +Txt−1 +Rεt

32. Introduction Small Model Great Recession Medium scale Conclusion
Expectations The Model Economy
Expectation Formation - Adaptive Learning
• Perceived Law of Motion - Agents' beliefs:
yt = at−1 +bt−1yt−1 +ct−1ωt
• Expected values of the model variables:
E∗
t yt+1 = at−1 +bt−1E∗
t yt +ct−1Etωt = at−1 +bt−1yt +ct−1B0ωt−1
• DSGE model can be represented as:
A0yt−1 +A1yt +A2E∗
t yt+1 +A3ωt = const
ωt −B0ωt−1 −B1εt = 0
• Adaptive Learning Equilibrium:
xt = µt−1 +Tt−1xt−1 +Rt−1εt
• Rational Expectations Equilibrium:
xt = µ +Txt−1 +Rεt

33. Introduction Small Model Great Recession Medium scale Conclusion
Simulations - collateral shockThe Model Economy
Simulated Model - Collateral Shock
0 5 10 15 20
-0.4
-0.3
-0.2
-0.1
0
0.1
0.2
wage
0 5 10 15 20
-2
-1.5
-1
-0.5
0
0.5
price of land
0 5 10 15 20
-0.2
-0.15
-0.1
-0.05
0
0.05
real loan rate
RE
AL - Ini Beliefs at first period
AL - Ini Beliefs at middle period
AL - Ini Beliefs at last period
0 5 10 15 20
-1.5
-1
-0.5
0
0.5
hours
0 5 10 15 20
-5
-4
-3
-2
-1
0
1
investment
0 5 10 15 20
-1
-0.8
-0.6
-0.4
-0.2
0
output
0 5 10 15 20
-0.5
-0.4
-0.3
-0.2
-0.1
0
0.1
price of capital
0 5 10 15 20
-6
-5
-4
-3
-2
-1
0
debt
0 5 10 15 20
-0.25
-0.2
-0.15
-0.1
-0.05
0
0.05
consumption
Pintus, Suda and Turgut (GRAPE) EXPECT 19.11.2018 13 / 25

34. Introduction Small Model Great Recession Medium scale Conclusion
Estimation method
Estimation
Approach
• Bayesian estimation using our self-developed MATLAB code:
• Both under Rational Expectations and Adaptive Learning
• Random Walk Metropolis Hasting algorithm (Serious issues under Adaptiv
Learning)
• Vector of estimated parameters:
• Structural: γh,γe,Ω,100(gγ −1),100(¯λq −1)
• Shock processes: ρa,ρz,ρνz ,ρq,ρνq ,ρϕ ,ρψ ,ρθ ,σa,σz,σνz ,σq,σνq ,σϕ ,σψ ,σ
• Gain parameter: g
• Fixed parameters: α = 0.3,n = 0.25,r = 1.01,θ = 0.75
• Data from 1975Q1 to 2010Q4

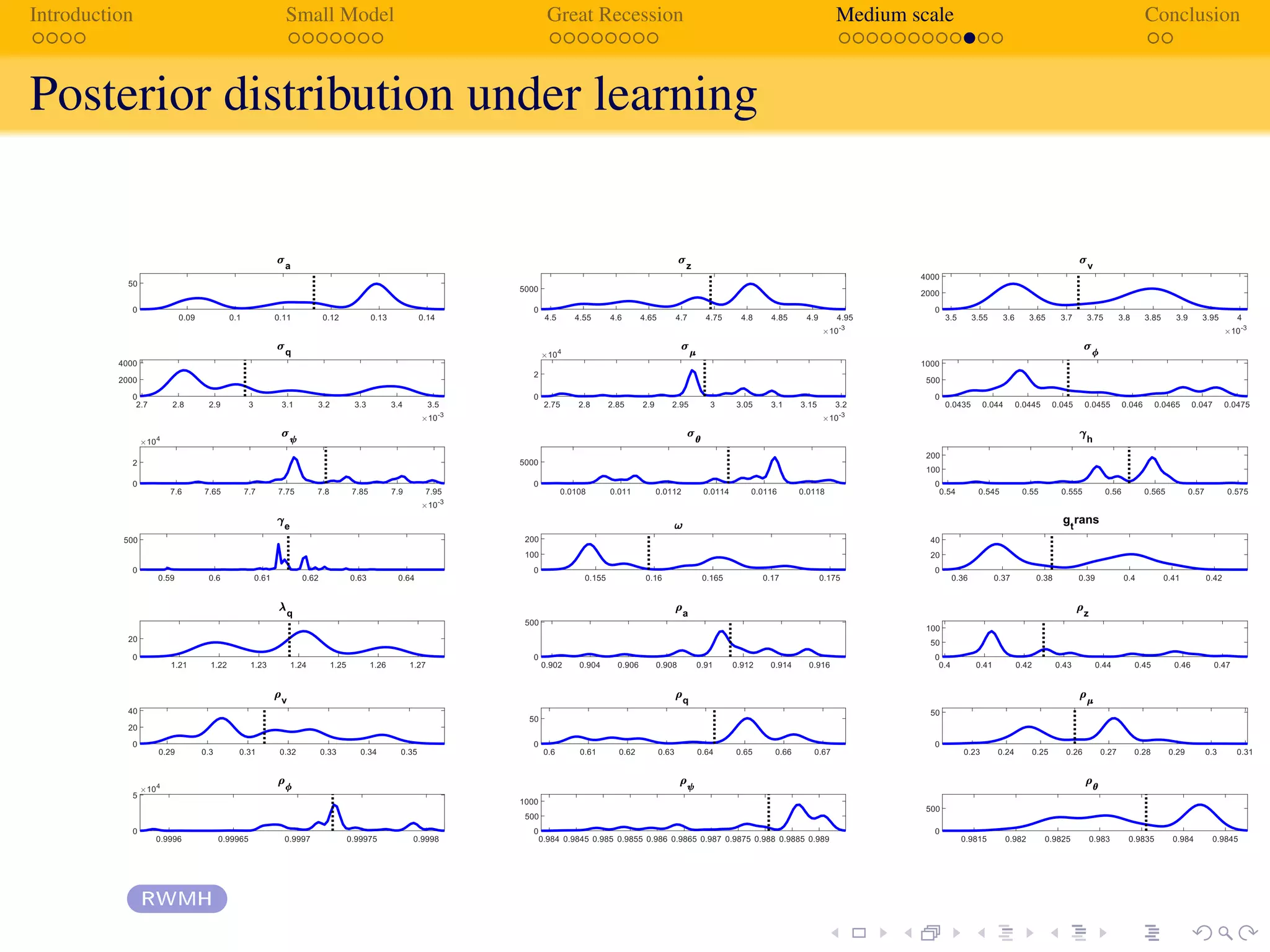
35. Introduction Small Model Great Recession Medium scale Conclusion
Estimation results Estimation
Results - Estimation
RE AL
Description Parameter Prior Posterior Mean Posterior Mean
Household Habit Persistency γh Beta 0.5122 [0.42,0.57] 0.5619 [0.55,0.57]
Entrepreneur Habit Persistency γe Beta 0.7924 [0.64,0.91] 0.6153 [0.61,0.62]
Investment Adjustment Cost Ω Gamma 0.1784 [0.15,0.21] 0.1595 [0.15,0.17]
Exo. Growth Rate gγ Gamma 0.3386 [0.27,0.45] 0.3817 [0.36,0.41]
SS Investment Specic Tech ¯λq Gamma 1.2919 [1.20,1.42] 1.2377 [1.21,1.28]
AR Patience ρa Beta 0.9340 [0.92,0.95] 0.9113 [0.90,0.92]
AR Perm. Technology ρz Beta 0.5560 [0.43,0.65] 0.4249 [0.40,0.47]
AR Trans. Technology ρvz Beta 0.3747 [0.08,0.61] 0.3141 [0.28,0.35]
AR Perm. Investment Tech ρq Beta 0.4810 [0.35,0.64] 0.6422 [0.60,0.67]
AR Trans. Investment Tech ρvq Beta 0.1523 [0.00,0.51] 0.2600 [0.23,0.29]
AR Land ρϕ Beta 1.0000 [1.00,1.00] 0.9997 [1.00,1.00]
AR Labor ρφ Beta 0.9987 [0.99,1.00] 0.9881 [0.99,0.99]
AR Collateral ρθ Beta 0.9879 [0.98,1.00] 0.9836 [0.98,0.98]
Std. Patience σa InvGamma 0.1404 [0.07,0.22] 0.1164 [0.08,0.14]
Std. Perm. Technology σz InvGamma 0.0038 [0.00,0.00] 0.0047 [0.00,0.00]
Std. Trans. Technology σvz InvGamma 0.0043 [0.00,0.00] 0.0037 [0.00,0.00]
Std. Perm. Investment Tech σq InvGamma 0.0042 [0.00,0.00] 0.0030 [0.00,0.00]
Std. Trans. Investment Tech σvq InvGamma 0.0022 [0.00,0.00] 0.0030 [0.00,0.00]
Std. Land σϕ InvGamma 0.0416 [0.04,0.05] 0.0451 [0.04,0.05]
Std. Labor σφ InvGamma 0.0069 [0.01,0.01] 0.0078 [0.01,0.01]
Std. Collateral σθ InvGamma 0.0109 [0.01,0.01] 0.0114 [0.01,0.01]
Gain g Gamma 0.0052 [0.01,0.01]
Log Marg. Likelihood 1940.3 1941.1
Pintus, Suda and Turgut (GRAPE) EXPECT 19.11.2018 15 / 25

36. Introduction Small Model Great Recession Medium scale Conclusion
Posterior distribution under learningEstimation
Posterior Distribution - Adaptive Learning
RWMH
Pintus, Suda and Turgut (GRAPE) EXPECT 19.11.2018 16 / 25

37. Introduction Small Model Great Recession Medium scale Conclusion
Evolution of beliefs Estimation
Beliefs yt = at−1 +bt−1yt−1 +ct−1ωt−1
0 20 40 60 80 100 120
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
Output
Land price
Capital price
Investment
Debt
0 20 40 60 80 100 120
-3
-2.5
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
Investment
Land price
Capital price
Investment
Debt
0 20 40 60 80 100 120
-1
-0.5
0
0.5
1
1.5
2
2.5
3
3.5
4
Land Price
Land price
Capital price
Investment
Debt
0 20 40 60 80 100 120
-8
-6
-4
-2
0
2
4
6
Debt
Land price
Capital price
Investment
Debt
Pintus, Suda and Turgut (GRAPE) EXPECT 19.11.2018 17 / 25

38. Introduction Small Model Great Recession Medium scale Conclusion
IRF under learning - collateral shockEstimation
IRFs - Collateral Shock
0 5 10 15 20
-0.4
-0.3
-0.2
-0.1
0
0.1
0.2
wage
0 5 10 15 20
-0.5
-0.4
-0.3
-0.2
-0.1
0
0.1
price of land
0 5 10 15 20
-0.2
-0.15
-0.1
-0.05
0
0.05
0.1
real loan rate
RE
AL - Beliefs at 2006Q1
AL - Beliefs at 2008Q4
0 5 10 15 20
-0.8
-0.6
-0.4
-0.2
0
0.2
hours
0 5 10 15 20
-4
-3
-2
-1
0
1
investment
0 5 10 15 20
-0.8
-0.6
-0.4
-0.2
0
output
0 5 10 15 20
-0.25
-0.2
-0.15
-0.1
-0.05
0
0.05
price of capital
0 5 10 15 20
-5
-4
-3
-2
-1
debt
0 5 10 15 20
-10
-8
-6
-4
-2
0
land of entrepreneur
Pintus, Suda and Turgut (GRAPE) EXPECT 19.11.2018 18 / 25

39. Introduction Small Model Great Recession Medium scale Conclusion
Conclusion
Use a RBC model with collateral-constrained borrowing.
Replace rational expectations with adaptive learning.
Consider updating of beliefs about financial shock process.
Find that learning considerably amplifies financial shocks and
helps explaining magnitude of the Great Recession.
Find that in larger estimated model learning still matters .

40. Introduction Small Model Great Recession Medium scale Conclusion
Conclusion cntd
Summary
• So far:
• First attempt to estimate DSGE model with housing and collatera
constraints under adaptive learning
• Time-varying transmission of housing and collateral shocks
• Next:
• Dierent algorithms for Bayesian estimation:
• Random block MH
• Sequential MH
• Alternative learning rules and initial-beliefs
• Kalman-lter learning and/or stochastic gradient
• Estimated initial beliefs - pre-sample OLS
• Implications for monetary and macro-prudential policies