Recommended
PDF
L'Écho du Nord - 26 octobre 2011
PPTX
DOC
PPT
PDF
PPTX
PDF
Gauchão 2014 escala de arbitragem 1ª rodada
PPSX
ODP
PPT
Lunchbox Learning - Get Financially Fit: Cash Flow
PPT
Lunchbox Learning: Learn How You Earn June 2013
PPTX
Dengue hemoragic fever (dhf)
KEY
Packetshader: A GPU-accelerated Software Routerを読んだ
PPTX
PDF
S&OP maturity comes prior to advance planning software
PDF
South bay native plants heucheras
PDF
CRYPT+YOU, UNDERSTAND TODAY!
PDF
PPT
PDF
RSA暗号運用でやってはいけない n のこと #ssmjp
PDF
KEY
PDF
PDF
PDF
#mailerstudy 02 暗号入門 (2012-02-22更新)
PDF
PDF
『データ解析におけるプライバシー保護』勉強会 秘密計算
PDF
PDF
PDF
Hacking demonstration 2018
More Related Content
PDF
L'Écho du Nord - 26 octobre 2011
PPTX
DOC
PPT
PDF
PPTX
PDF
Gauchão 2014 escala de arbitragem 1ª rodada
PPSX
Viewers also liked
ODP
PPT
Lunchbox Learning - Get Financially Fit: Cash Flow
PPT
Lunchbox Learning: Learn How You Earn June 2013
PPTX
Dengue hemoragic fever (dhf)
KEY
Packetshader: A GPU-accelerated Software Routerを読んだ
PPTX
PDF
S&OP maturity comes prior to advance planning software
PDF
South bay native plants heucheras
Similar to 20120922 勉強会スライド
PDF
CRYPT+YOU, UNDERSTAND TODAY!
PDF
PPT
PDF
RSA暗号運用でやってはいけない n のこと #ssmjp
PDF
KEY
PDF
PDF
PDF
#mailerstudy 02 暗号入門 (2012-02-22更新)
PDF
PDF
『データ解析におけるプライバシー保護』勉強会 秘密計算
PDF
PDF
PDF
Hacking demonstration 2018
PPT
PDF
PDF
暗号化の歴史と技術 〜古代の暗号から次世代の暗号技術について〜
PDF
[Basic 14] 暗号について / RSA 暗号 / 楕円曲線暗号
PDF
ElGamal型暗号文に対する任意関数演算・再暗号化の二者間秘密計算プロトコルとその応用
PDF
20120922 勉強会スライド 1. 2. 3. 4. 5. 6. 7. 8. ブルートフォース攻撃
別名、総当たり攻撃
シーザー暗号に適用する場合、25通りの文字のス
ライドを全て試す
IRGVCTX JSHWDUY KTIXEVZ LUJYFWA MVKZGXB NWLAHYC
OXMBIZD PYNCJAE QZODKBF RAPELCG SBQFMDH
TCRGNEI UDSHOFJ VETIPGK WFUJQHL XGVKRIM
YHWLSJN ZIXMTKO AJYNULP BKZOVMQ CLAPWNR
DMBQXOS ENCRYPT FODSZQU GPETARV
全ての組み合わせを検証した結果、-3のスライドでENCRYPTが出現
9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. XORのおさらい
Exclusive OR
排他的論理和
0 xor 0 -> 0 例えば
0 xor 1 -> 1 0 1 00 1 0 1 0 1 0 1
1 0 1 00 1 00 1 1 0
1 xor 0 -> 1
↓
1 xor 1 -> 0
1 1 1 0 1 1 1 00 1 1
20. 21. 暗号化思想の変化
過去: とアルゴリズムは同じくらい重要な秘密
現在:アルゴリズムは公開し、強さを検証されるべ
き
アルゴリズムが解っても、 が解らなくては復
号化できないことが重要
DESは、強いアルゴリズムではなくなってしまった
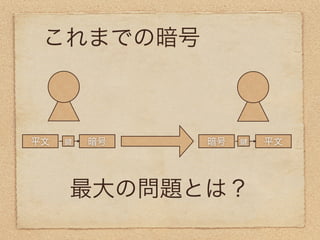
22. 23. 24. 25. 26. 27. 28. 公開 暗号
暗号化の を公開する暗号
ただし、暗号化に使用する と復号化
に使用する は別物
従来の暗号の最大の弱点であった、
の共有問題を解決することが出来る!
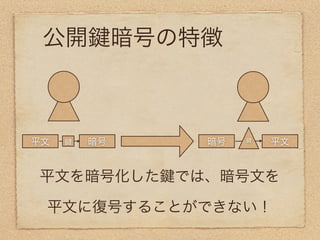
29. 公開 暗号の特徴
平文 暗号 暗号 平文
平文を暗号化した では、暗号文を
平文に復号することができない!
30. RSA暗号
公開 暗号として、現在最も使用されている実装
その暗号の強度の保証に、素数のかけ算と素因数分解の不可逆性を
使用している
アルゴリズム:二つの素数を掛け合わせた巨大な合成数による剰余
計算
:二つの巨大な素数をp,qとし、N=pgとする
暗号 :N、LCM(p-1,q-1)=Lと互いに素である2以上L未満の数
復号 :N、DE mod L = 1 を満たす、2以上L未満の数D
31. RSA暗号の仕組み
暗号化
公開 ペアE,Nを使って次の計算をする
C = ME mod N
復号化
秘密 ペアD,Nを使って次の計算をする
M = CD mod N
32. なぜRSAは を公開できるのか
C= ME mod N
M= C D mod N
攻撃するには、公開 から秘密 を割り出すこと
が出来ればいい
EとNから、Dを求めることが可能か?
実はそれがメチャクチャ難しいことが、RSA
の安全性の根拠なのです
33. ペアのおさらい
N = pq (pとqは、巨大な素数)
L は p-1 と q-1 の最小公倍数
Eは 1 < E < Lとなる、EとLの最大公約数が1とな
る数字(互いに素)
Dは、1 < D < Lとなる、ED mod L = 1 を満たす
数
34. EとNからDを求めるには
C = ME mod Nを逆算する
この計算は、離散対数を求めるという非常に難しい問題
ED mod L = 1 を解く
しかし、Lは公開されていない(pとqがわからない)
Nからpとqを求める
二つの素数からなる合成数を素因数分解するとは難しい
一方向性関数という、逆算が困難な計算
35. を公開することによる問題
暗号化の は、誰もが知ることが可能
つまり、暗号の送信者へのなりすましが
可能である
Man in the Middle 攻撃という
どのようにして、送信者を保証するのか?
36. 公開 暗号の副産物
電子署名が可能になる
秘密 を公開する
方法:秘密 を公開し、公開 で任意の文字列を暗号化
する
誰でも復号出来るが、暗号化できるのは暗号 を
持っている人のみ
実際は、認証局と呼ばれる十分に信用できる組織が行う
37. 公開 暗号、その欠点
公開 暗号の致命的欠点
計算速度が、圧倒的に遅い
に用いられる素数の桁数が、文字通り桁違い
圧倒的な計算速度を誇るコンピュータですら、計算に時
間がかかる
それはつまり……
普通に平文を暗号化していては、とても実用に耐えない
38. 39. 40. One time pad 暗号
平文と同じ長さの を用意してXORを
かけることにより、原理的に解読が不
可能な暗号を創り出せる
致命的欠点: の生成と交換
41. 42. Editor's Notes #2 \n #3 \n #4 \n #5 \n #6 \n #7 \n #8 \n #9 \n #10 \n #11 \n #12 \n #13 \n #14 \n #15 \n #16 \n #17 \n #18 \n #19 \n #20 \n #21 &#x3053;&#x306E;&#x8FBA;&#x3067;&#x3001;&#x307B;&#x304B;&#x306E;&#x89E3;&#x8AAD;&#x65B9;&#x6CD5;&#x3082;&#x3044;&#x308D;&#x3044;&#x308D;&#x3068;&#x89E6;&#x308A;&#x3060;&#x3051;&#x4F1D;&#x3048;&#x308B;\n #22 \n #23 \n #24 \n #25 \n #26 \n #27 \n #28 \n #29 \n #30 \n #31 \n #32 \n #33 &#x6697;&#x53F7;&#x3068;&#x5FA9;&#x53F7;&#x306E;&#x6570;&#x5B66;&#x7684;&#x6839;&#x62E0;&#x306F;&#x3072;&#x3068;&#x307E;&#x305A;&#x6B63;&#x3057;&#x3044;&#x3068;&#x3057;&#x3066;&#x304A;&#x304F;\n #34 \n #35 \n #36 \n #37 \n #38 \n #39 \n #40 \n #41 \n #42 \n #43 \n