Best-first search is a heuristic search algorithm that expands the most promising node first. It uses an evaluation function f(n) that estimates the cost to reach the goal from each node n. Nodes are ordered in the fringe by increasing f(n). A* search is a special case of best-first search that uses an admissible heuristic function h(n) and is guaranteed to find the optimal solution.

1. 1
Heuristic Search
(Where we try to choose smartly)

2. 2
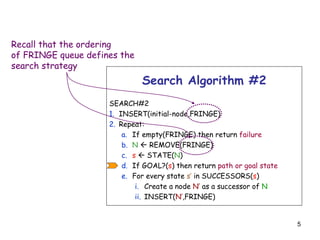
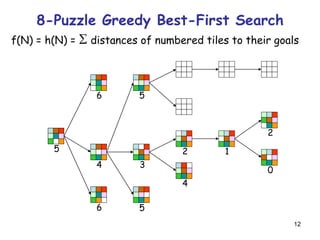
Best-First Search
 It exploits state description to estimate
how “good” each search node is
 An evaluation function f maps each node
N of the search tree to a real number
f(N)  0
[Traditionally, f(N) is an estimated cost; so, the smaller
f(N), the more promising N]
 Best-first search sorts the FRINGE in
increasing f
[Arbitrary order is assumed among nodes with equal f]

3. 3
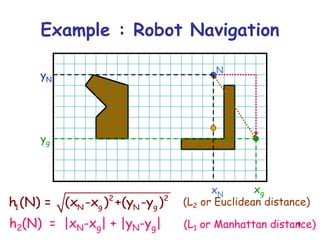
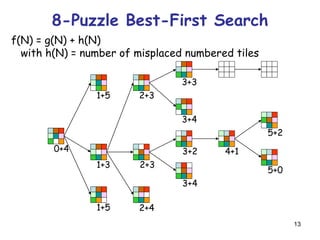
Best-First Search
 It exploits state description to estimate
how “good” each search node is
 An evaluation function f maps each node
N of the search tree to a real number
f(N)  0
[Traditionally, f(N) is an estimated cost; so, the smaller
f(N), the more promising N]
 Best-first search sorts the FRINGE in
increasing f
[Arbitrary order is assumed among nodes with equal f]
“Best” does not refer to the quality
of the generated path
Best-first search does not generate
optimal paths in general

4. • Idea: use an evaluation function f(n) for each node
– estimate of "desirability"
Expand most desirable unexpanded node
• Implementation:
Order the nodes in fringe in increasing order of
desirability
• Special cases:
– greedy best-first search
– A* search

5. 5
Search Algorithm #2
SEARCH#2
1. INSERT(initial-node,FRINGE)
2. Repeat:
a. If empty(FRINGE) then return failure
b. N  REMOVE(FRINGE)
c. s  STATE(N)
d. If GOAL?(s) then return path or goal state
e. For every state s’ in SUCCESSORS(s)
i. Create a node N’ as a successor of N
ii. INSERT(N’,FRINGE)
Recall that the ordering
of FRINGE queue defines the
search strategy

6. 6
 Typically, f(N) estimates:
• either the cost of a solution path through N
Then f(N) = g(N) + h(N), where
– g(N) is the cost of the path from the initial node to N
– h(N) is an estimate of the cost of a path from N to a goal node
• or the cost of a path from N to a goal node
Then f(N) = h(N)  Greedy best-search
 But there are no limitations on f. Any function
of your choice is acceptable.
But will it help the search algorithm?
How to construct f?

7. 7
 Typically, f(N) estimates:
• either the cost of a solution path through N
Then f(N) = g(N) + h(N), where
– g(N) is the cost of the path from the initial node to N
– h(N) is an estimate of the cost of a path from N to a goal node
• or the cost of a path from N to a goal node
Then f(N) = h(N)
 But there are no limitations on f. Any function
of your choice is acceptable.
But will it help the search algorithm?
How to construct f?
Heuristic function

8. 8
 The heuristic function h(N)  0 estimates
the cost to go from STATE(N) to a goal state
it depends only on STATE(N) and the goal
GOAL state.
 the heuristic tells us approximately how far
the state is from the goal state
• Note we said “approximately”. Heuristics
might underestimate or overestimate the
merit of a state.
Heuristic Function

9. 9
Example : Robot Navigation
xN
yN
N
xg
yg
2 2
g g1 N Nh (N) = (x -x ) +(y -y ) (L2 or Euclidean distance)
h2(N) = |xN-xg| + |yN-yg| (L1 or Manhattan distance)

10. 10
 h1(N) = number of misplaced numbered tiles = 6
 h2(N) = sum of the (Manhattan) distance of
every numbered tile to its goal position
= 2 + 3 + 0 + 1 + 3 + 0 + 3 + 1 = 13
 h3(N) = sum of permutation inversions
= n5 + n8 + n4 + n2 + n1 + n7 + n3 + n6
= 4 + 6 + 3 + 1 + 0 + 2 + 0 + 0
= 16
Example
14
7
5
2
63
8
STATE(N)
64
7
1
5
2
8
3
Goal state

11. 11
8-Puzzle Greedy Best-First Search
4
5
5
3
3
4
3 4
4
2 1
2
0
3
4
3
f(N) = h(N) = number of misplaced numbered tiles
The white tile is the empty tile

12. 12
5
6
6
4
4
2 1
2
0
5
5
3
8-Puzzle Greedy Best-First Search
f(N) = h(N) = S distances of numbered tiles to their goals

13. 13
0+4
1+5
1+5
1+3
3+3
3+4
3+4
3+2 4+1
5+2
5+0
2+3
2+4
2+3
8-Puzzle Best-First Search
f(N) = g(N) + h(N)
with h(N) = number of misplaced numbered tiles

14. Heuristics for 8-puzzle I
•The number of
misplaced tiles
(Hamming
Distance)
1 2 3
4 5 6
7 8
1 2 3
4 5 6
7 8
1 2 3
4 5 6
7 8
1 2 3
4 5 6
7 8
In this case, only “8” is misplaced, so the
heuristic function evaluates to 1.
In other words, the heuristic is telling us, that it thinks
a solution might be available in just 1 more move.
Goal
State
Current
State
Notation: h(n) h(current state) = 1

15. Heuristics for 8-puzzle II
•The Manhattan
Distance (not
including the
blank)
In this case, only the “3”, “8” and “1” tiles are
misplaced, by 2, 3, and 3 squares respectively,
so the heuristic function evaluates to 8.
In other words, the heuristic is telling us, that it thinks
a solution is available in just 8 more moves.
3 2 8
4 5 6
7 1
1 2 3
4 5 6
7 8
Goal
State
Current
State
3 3
8
8
1
1
2 spaces
3 spaces
3 spaces
Total 8
Notation: h(n) h(current state) = 8

16. Properties of greedy best-first
search
• Complete? No
• Time? O(bm), but a good heuristic can
give dramatic improvement
• Space? O(bm) -- keeps all nodes in
memory
• Optimal? No
 m is the maximum depth of the search

17. Hill Climbing
 a local search Algorithm
 keep a single "current" state, try to improve it
 Estimates how far away the goal is.
 Is neither optimal nor complete.
 Can be very fast.
Local (a.k.a. “incremental improvement”) search
Another approach to search involves starting with
an initial guess at a solution and gradually
improving it until it is one.

18. 1 2 3
4 5
7 8 6
1 2 3
4 5
7 8 6
1 3
4 2 5
7 8 6
1 2
4 5 3
7 8 6
1 2 3
4 5 6
7 8
1 2 3
4 5
7 8 6
1 2 3
4 8 5
7 6
1 2 3
4 8 5
7 6
1 2 3
4 8 5
7 6
1 2
4 8 3
7 6 5
1 2 3
4 8
7 6 5
5
6 4
3
4 2
1 3 3
0 2
 This is “hill climbing”
 We can use
heuristics to guide
“hill climbing” search.
 In this example, the
Manhattan Distance
heuristic helps us
quickly find a solution
to the 8-puzzle.
But “hill climbing has a
problem...”
h(n)

19. 1 2 3
4 5 8
6 7
1 2 3
4 5
6 7 8
1 2 3
4 5 8
6 7
1 2 3
4 5
6 7 8
1 2
4 5 3
6 7 8
6
7 5
6 6
In this example,
hill climbing does
not work!
All the nodes on
the fringe are
taking a step
“backwards”
(local minima)
Note that this
puzzle is solvable
in just 12 more
steps.
h(n)

20. Hill climbing on a surface of states
Height Defined by
Evaluation Function
Problem : local maxima or minima based on h
definition ( positive or negative h ) , because
there might be a general min or max.

21. Hill-climbing search
Hill Climbing Algorithm
currentNode = startNode;
loop do
L = NEIGHBORS(currentNode);
nextEval = INF;
nextNode = NULL;
for all neighbor in L
if (EVAL(neighbor) < nextEval)
nextNode = neighbor;
nextEval = EVAL(neighbor);
if nextEval >= EVAL(currentNode)
//Return current node since no better neighbors exist
return currentNode;
currentNode = nextNode;
Finds node with
min heuristic
value
nextEval has min h
so if it is bigger ,
any other node
is bigger

22. 22
Admissible Heuristic
 Let h*(N) be the cost of the optimal path
from N to a goal node
 The heuristic function h(N) is admissible
if:
0  h(N)  h*(N)
 An admissible heuristic function is always
optimistic !

23. 23
Admissible Heuristic
 Let h*(N) be the cost of the optimal path
from N to a goal node
 The heuristic function h(N) is admissible
if:
0  h(N)  h*(N)
 An admissible heuristic function is always
optimistic !
G is a goal node  h(G) = 0

24. 24
 h1(N) = number of misplaced tiles = 6
is ???
 h2(N) = sum of the (Manhattan) distances of
every tile to its goal position
= 2 + 3 + 0 + 1 + 3 + 0 + 3 + 1 = 13
is admissible
 h3(N) = sum of permutation inversions
= 4 + 6 + 3 + 1 + 0 + 2 + 0 + 0 = 16
is not admissible
8-Puzzle Heuristics
14
7
5
2
63
8
STATE(N)
64
7
1
5
2
8
3
Goal state

25. 25
 h1(N) = number of misplaced tiles = 6
is admissible
 h2(N) = sum of the (Manhattan) distances of
every tile to its goal position
= 2 + 3 + 0 + 1 + 3 + 0 + 3 + 1 = 13
is ???
 h3(N) = sum of permutation inversions
= 4 + 6 + 3 + 1 + 0 + 2 + 0 + 0 = 16
is not admissible
8-Puzzle Heuristics
14
7
5
2
63
8
STATE(N)
64
7
1
5
2
8
3
Goal state

26. 26
 h1(N) = number of misplaced tiles = 6
is admissible
 h2(N) = sum of the (Manhattan) distances of
every tile to its goal position
= 2 + 3 + 0 + 1 + 3 + 0 + 3 + 1 = 13
is admissible
 h3(N) = sum of permutation inversions
= 4 + 6 + 3 + 1 + 0 + 2 + 0 + 0 = 16
is ???
8-Puzzle Heuristics
14
7
5
2
63
8
STATE(N)
64
7
1
5
2
8
3
Goal state

27. 27
 h1(N) = number of misplaced tiles = 6
is admissible
 h2(N) = sum of the (Manhattan) distances of
every tile to its goal position
= 2 + 3 + 0 + 1 + 3 + 0 + 3 + 1 = 13
is admissible
 h3(N) = sum of permutation inversions
= 4 + 6 + 3 + 1 + 0 + 2 + 0 + 0 = 16
is not admissible
8-Puzzle Heuristics
14
7
5
2
63
8
STATE(N)
64
7
1
5
2
8
3
Goal state

28. 28
Robot Navigation Heuristics
Cost of one horizontal/vertical step = 1
Cost of one diagonal step = 2
2 2
g g1 N Nh (N) = (x -x ) +(y -y ) is admissible

29. 29
Robot Navigation Heuristics
Cost of one horizontal/vertical step = 1
Cost of one diagonal step = 2
h2(N) = |xN-xg| + |yN-yg| is ???

30. 30
Robot Navigation Heuristics
Cost of one horizontal/vertical step = 1
Cost of one diagonal step = 2
h2(N) = |xN-xg| + |yN-yg| is admissible if moving along
diagonals is not allowed, and
not admissible otherwiseh*(I) = 42
h2(I) = 8

31. 31
How to create an admissible h?
 An admissible heuristic can usually be seen as
the cost of an optimal solution to a relaxed
problem (one obtained by removing constraints)
 In robot navigation:
• The Manhattan distance corresponds to removing the
obstacles
• The Euclidean distance corresponds to removing both
the obstacles and the constraint that the robot
moves on a grid
 More on this topic later

32. 32
 By solving relaxed problems at each node
 In the 8-puzzle, the sum of the distances of
each tile to its goal position (h2) corresponds to
solving 8 simple problems:
How to create an admissible h?
14
7
5
2
63
8
64
7
1
5
2
8
3
5
5
di is the length of the
shortest path to move
tile i to its goal position,
ignoring the other tiles,
e.g., d5 = 2
h2 = Si=1,...8 di

33. 33
A* Search
(most popular algorithm in AI)
1) f(N) = g(N) + h(N), where:
• g(N) = cost of best path found so far to N
• h(N) = admissible heuristic function
2) for all arcs: cost(N,N’)   > 0
3) SEARCH#2 algorithm is used
 Best-first search is then called A* search

34. 34
Result #1
A* is complete and optimal

35. Optimality of A* (proof)
• Suppose some non-optimal goal G2 has been generated and is in
the fringe. Let n be an unexpanded node in the fringe such that
n is on a shortest path to an optimal goal G.
• f(G2) = g(G2) since h(G2) = 0
• g(G2) > g(G) since G2 is suboptimal
• f(G) = g(G) since h(G) = 0
• f(G2) > f(G) from above

36. Optimality of A* (proof)
• Suppose some non-optimal goal G2 has been generated and is in
the fringe. Let n be an unexpanded node in the fringe such that
n is on a shortest path to an optimal goal G.
• f(G2) > f(G) from above
• h(n) ≤ h^*(n) since h is admissible
• g(n) + h(n) ≤ g(n) + h*(n) =f(G)
• f(n) ≤ f(G)
Hence f(G2) > f(n), and A* will never select G2 for expansion

37. Properties of A*
• Complete? Yes (unless there are
infinitely many nodes.)
• Time? Exponential
• Space? Keeps all nodes in memory
• Optimal? Yes

38. 38
Time Limit Issue
 When a problem has no solution, A* runs for ever if
the state space is infinite. In other cases, it may take
a huge amount of time to terminate
 So, in practice, A* is given a time limit. If it has not
found a solution within this limit, it stops. Then there
is no way to know if the problem has no solution, or if
more time was needed to find it
 When AI systems are “small” and solving a single
search problem at a time, this is not too much of a
concern.
 When AI systems become larger, they solve many
search problems concurrently, some with no solution.
What should be the time limit for each of them?
This is a complicated work.

39. 39
8-Puzzle
0+4
1+5
1+5
1+3
3+3
3+4
3+4
3+2 4+1
5+2
5+0
2+3
2+4
2+3
f(N) = g(N) + h(N)
with h(N) = number of misplaced tiles

40. A Worked Example: Maze Traversal
1 2 3 4 5
A
B
D
C
E
Problem: To get from square A3 to square
E2, one step at a time, avoiding obstacles
(black squares).
Operators: (in order)
•go_left(n)
•go_down(n)
•go_right(n)
each operator costs 1.
Heuristic: Manhattan distance

41. Operators: (in order)
•go_left(n)
•go_down(n)
•go_right(n)
each operator costs 1.
A2
A3
B3 A4g(A2) = 1
h(A2) = 4
g(B3) = 1
h(B3) = 4
g(A4) = 1
h(A4) = 6
1 2 3 4 5
A
B
D
C
E
A2
B3
A4

42. Operators: (in order)
•go_left(n)
•go_down(n)
•go_right(n)
each operator costs 1.
A2
A3
B3 A4g(A2) = 1
h(A2) = 4
g(B3) = 1
h(B3) = 4
g(A4) = 1
h(A4) = 6
A1 g(A1) = 2
h(A1) = 5
1 2 3 4 5
A
B
D
C
E
A2
B3
A1 A4

43. Operators: (in order)
•go_left(n)
•go_down(n)
•go_right(n)
each operator costs 1.
A2
A3
B3 A4g(A2) = 1
h(A2) = 4
g(B3) = 1
h(B3) = 4
g(A4) = 1
h(A4) = 6
C3 B4g(C3) = 2
h(C3) = 3
g(B4) = 2
h(B4) = 5
A1 g(A1) = 2
h(A1) = 5
1 2 3 4 5
A
B
D
C
E
A2
B3
A4A1
C3
B4

44. Operators: (in order)
•go_left(n)
•go_down(n)
•go_right(n)
each operator costs 1.
A2
A3
B3 A4g(A2) = 1
h(A2) = 4
g(B3) = 1
h(B3) = 4
g(A4) = 1
h(A4) = 6
C3 B4g(C3) = 2
h(C3) = 3
g(B4) = 2
h(B4) = 5
A1 g(A1) = 2
h(A1) = 5
1 2 3 4 5
A
B
D
C
E
B1 g(B1) = 3
h(B1) = 4
A2
B3
A4A1
B1
C3
B4

45. Operators: (in order)
•go_left(n)
•go_down(n)
•go_right(n)
each operator costs 1.
A2
A3
B3 A4g(A2) = 1
h(A2) = 4
g(B3) = 1
h(B3) = 4
g(A4) = 1
h(A4) = 6
C3 B4g(C3) = 2
h(C3) = 3
g(B4) = 2
h(B4) = 5
A1 g(A1) = 2
h(A1) = 5
1 2 3 4 5
A
B
D
C
E
B1 g(B1) = 3
h(B1) = 4
B5 g(B5) = 3
h(B5) = 6
A2
B3
A4A1
B1
C3
B4 B5

46. 46
Heuristic Accuracy
Let h1 and h2 be two consistent heuristics such
that for all nodes N:
h1(N)  h2(N)
h2 is said to be more accurate (or more informed)
than h1
 h1(N) = number of misplaced
tiles
 h2(N) = sum of distances of
every tile to its goal position
 h2 is more accurate than h1
14
7
5
2
63
8
STATE(N)
64
7
1
5
2
8
3
Goal state

47. 47
What to do with revisited states?
c = 1
100
2
1
2
h = 100
0
90
1

48. 48
What to do with revisited states?
c = 1
100
2
1
2
h = 100
0
90
1
104
4+90
f = 1+100 2+1
?
If we discard this new node, then the search
algorithm expands the goal node next and
returns a non-optimal solution

49. 49
1
100
2
1
2
100
0
90
1
104
4+90
1+100 2+1
2+90
102
Instead, if we do not discard nodes revisiting
states, the search terminates with an optimal
solution
What to do with revisited states?

50. 50
But ...
If we do not discard nodes revisiting
states, the size of the search tree can be
exponential in the number of visited states
1
2
11
1
2
1
1
1+1 1+1
2+1 2+1 2+1 2+1
4 4 4 4 4 4 4 4

51. 51
But ...
If we do not discard nodes revisiting
states, the size of the search tree can be
exponential in the number of visited states
1
2
11
1
2
1
1
2n+1 states
1+1 1+1
2+1 2+1 2+1 2+1
4 4 4 4 4 4 4 4
O(2n) nodes

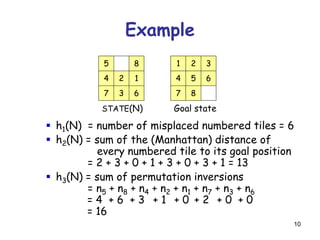
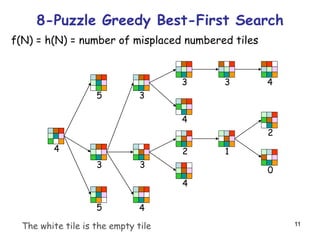
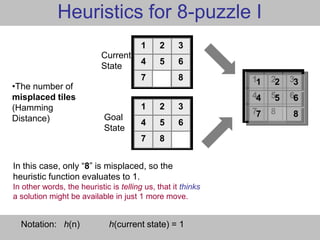
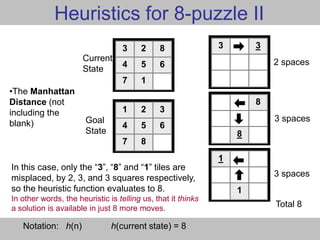
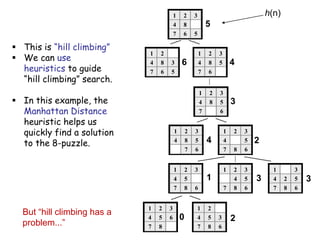
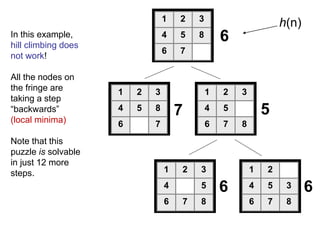
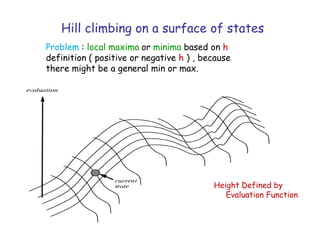
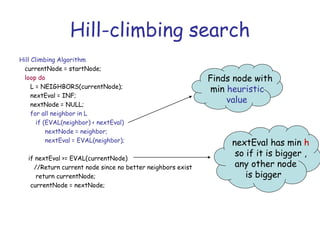
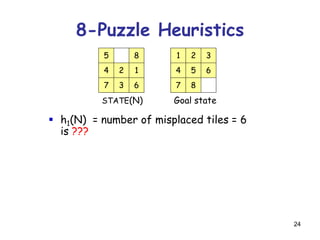
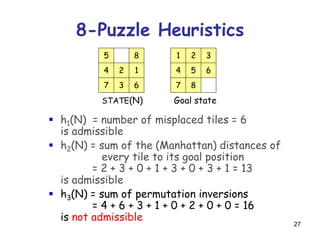
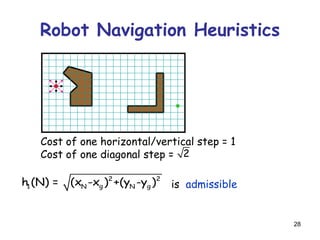
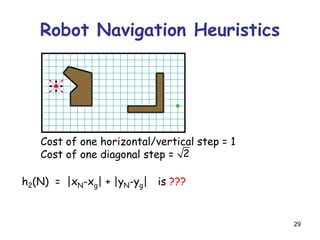
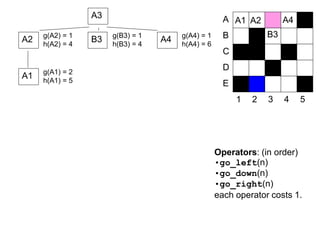
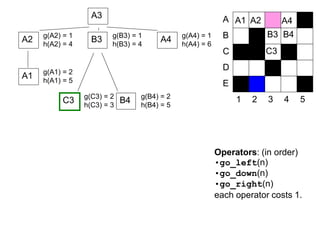
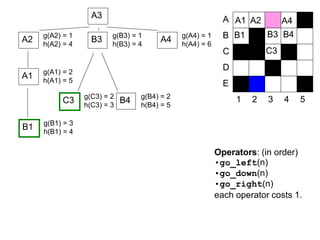
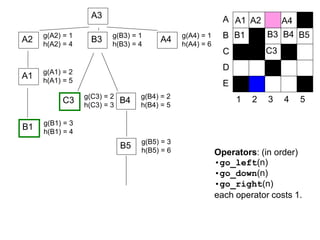
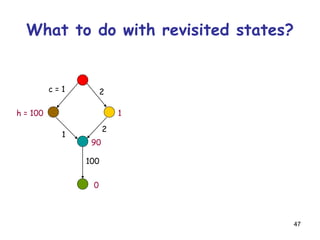
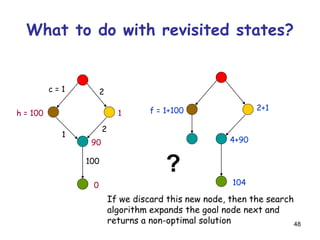
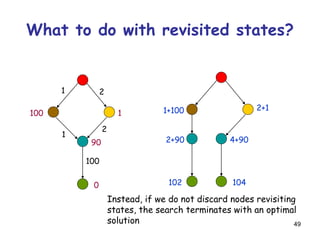
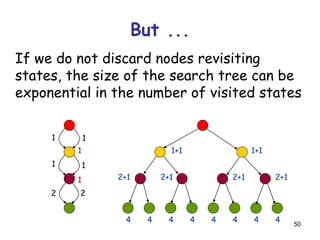
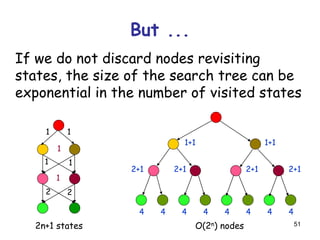
52. 52
 It is not harmful to discard a node revisiting
a state if the cost of the new path to this
state is  cost of the previous path
[so, in particular, one can discard a node if it re-visits
a state already visited by one of its ancestors]
 A* remains optimal, but states can still be re-
visited multiple times
[the size of the search tree can still be exponential in
the number of visited states]

53. Application
• Virus Scanning
• In virus scanning, an algorithm searches for
key pieces of code associated with particular
kinds or viruses, reducing the number of files
that need to be scanned. One of the benefits
of heuristic virus scanning is that different
viruses of the same family can be detected
without being known due to the common code
markers
53

54. • Virus identification is a balance between
two imperatives: the avoidance of false
negatives (the scanner fails to detect
an infection) and false positives (the
scanner detects a virus where none
exists).
• All levels of heuristic analysis add
processing overhead to scanning time,
and for some products, the slower
performance can be all too obvious.
54

55. THANKS FOR LISTENING
ANY QUESTIONS ?
55