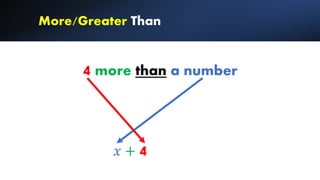
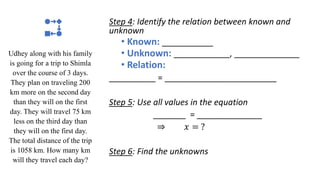
The document provides a comprehensive guide for eighth-grade students on translating word problems into algebraic expressions. It includes examples of mathematical operations such as addition, subtraction, multiplication, and division, along with real-life application problems that require comparisons and the identification of independent and dependent variables. Finally, it outlines a systematic 6-step approach to solving word problems, ensuring students can tackle various scenarios effectively.

1. WORD PROBLEMS CLASS 8

2. TEST YOURSELF
English Phrases Algebraic Translation
Three times a number increased by four is
subtracted from two times the same
number.
Five times a number increased by four is
divided by six times the same number.

3. OBJECTIVES
Read and translate word
problems.
Identify problems involving
comparisons.
Solve the problems in just
6 steps

4. KEYWORDS

5. KEYWORDS

6. KEYWORDS

7. More/Greater Than
4 more than a number
𝑥𝑥 + 4

8. Less/fewer Than
4 less than a number
𝑥𝑥 − 4

9. Subtracted From
4 is subtracted from a number
𝑥𝑥 − 4

10. ADDITION (+)
English Words English Phrases Algebraic Translation
sum The sum of a number and 4 𝑥𝑥 + 4
more than 4 more than a number 𝑥𝑥 + 4
increased A number increased by 4 𝑥𝑥 + 4
greater than 4 greater than a number 𝑥𝑥 + 4
Plus A number plus 4 𝑥𝑥 + 4
added to A number added to 4 𝑥𝑥 + 4

11. SUBTRACTION (−)
English Words English Phrases Algebraic Translation
difference
The difference between a
number and 4
𝑥𝑥 − 4
less than 4 less than a number 𝑥𝑥 − 4
decreased A number decreased by 4 𝑥𝑥 − 4
fewer than 4 fewer than a number 𝑥𝑥 − 4
minus A number minus 4 𝑥𝑥 − 4
subtracted 4 subtracted from a number 𝑥𝑥 − 4
less A number less 4 𝑥𝑥 − 4

12. MULTIPLICATION (×)
English Words English Phrases Algebraic Translation
product
The product of a
number and 4
4𝑥𝑥
times 4 times a number 4𝑥𝑥
of 4 of a number 4𝑥𝑥

13. TIMES (×)
English Words English Phrases Algebraic Translation
Double or twice Twice a number 2𝑥𝑥
triple or thrice Thrice a number 3𝑥𝑥

14. FRACTIONAL PART
English Words English Phrases Algebraic Translation
half half of the number
1
2
𝑥𝑥
One forth One forth of the number
1
4
𝑥𝑥
Two third Two third of the number
2
3
𝑥𝑥

15. DIVISION (÷)
English Words English Phrases Algebraic Translation
divided by
A number divided
by 4
𝑥𝑥
4
quotient
The quotient of a
number and 4
𝑥𝑥
4

16. EQUAL (=)
English Words English Phrases Algebraic Translation
is (or was, will be) A number plus 4 is 6. 𝑥𝑥 + 4 = 6
equals
A number plus 9 equals
15
𝑥𝑥 + 9 = 15

17. PRACTICE
English Phrases Algebraic Translation
5 more than a number
a number increased by 7
one-third of a number
A number times 9
half of the number

18. PRACTICE
English Phrases Algebraic Translation
a number subtract 10
10 subtracted from a number
10 less than a number
a number divided by 6
6 divided by a number

19. PRACTICE
English Phrases Algebraic Translation
A number subtract 15
A number subtracted from 15
15 less than a number
15 divided by a number

20. PRACTICE
English Phrases Algebraic Translation
double a number added to 15
one-fifth a number plus 17
6 times a number is taken from 12.
1.2 times a number plus 1
1.2 times the sum of a number and 1.

21. Let x be the amount of money Guri has. Write an algebraic expression for
each of the following.
(NOTE: Just write an algebraic expression. There is nothing to solve.)
English Phrases Algebraic Translation
Manjit has ₹6 less than Guri has.
Sukhjit has 3 times as much money as Guri.
Guneet has ₹5 more than Guri.

22. Let x the number miles Harsh drove. Write an algebraic expression for
each of the following.
(NOTE: Just write an algebraic expression. There is nothing to solve.)
English Phrases Algebraic Translation
Raman drove twice as far as Harsh drove.
Harman drove 12 miles less than Harsh drove.
Navi drove 17 miles more than Harsh drove.

23. COMPARISONS
• Jasreet has 11 fewer dresses than Harman. If Harman has 16 dresses,
how may dresses does Jasreet have?
• Ekam has 9 turbans. Sachkirat has 5 more turbans than Ekam. How
many turbans does Sachkirat have?
• Harkamal has 3 times as many bracelets as Taran. Taran has 2
bracelets. How many bracelets does Harkamal have?
• The length of Amrit’s back yard is four times the width. Width of the
back yard is 100 square meter. Find the length of the back yard.

24. Dependent Vs Independent
• Jasreet has 11 fewer dresses than Harman. If Harman has 16 dresses,
how may dresses does Jasreet have?
• Ekam has 9 turbans. Sachkirat has 5 more turbans than Ekam. How
many turbans does Sachkirat have?
• Harkamal has 3 times as many bracelets as Taran. Taran has 2
bracelets. How many bracelets does Harkamal have?
• The length of Amrit’s back yard is four times the width. Width of the
back yard is 100 square meter. Find the length of the back yard.

25. 6 STEPS TO SOLVE THE COMPARISON PROBLEMS
Find Find the unknowns
Use Use all values in the equation
Relate Identify the relation between known and unknown
Let Let the independent and dependent
Compare Identify the comparison statement
Identify Identify what you are looking for

26. PROBLEM - I
Chhavi wants to fence in a
rectangular region to be used for
gardening. Its length is 4 times
the width. If the perimeter of
the rectangle is 180 feet, what
are the dimensions of the
rectangle?

27. Chhavi wants to fence in a rectangular
region to be used for gardening. Its
length is 4 times the width. If the
perimeter of the rectangle is 180 feet,
what are the dimensions of the
rectangle?
Step 1: Identify what you are
looking for
_____________________
Step 2: Identify the comparison
statement
_____________________
Step 3: Let the Independent and
dependent
_________ = ____________
_________ = ____________

28. Chhavi wants to fence in a rectangular
region to be used for gardening. Its
length is 4 times the width. If the
perimeter of the rectangle is 180 feet,
what are the dimensions of the
rectangle?
Step 1: Identify what you are
looking for
Length, width
Step 2: Identify the comparison
statement
Length is 4 times the width
Step 3: Let the Independent and
dependent
Width = 𝒙𝒙
Length = 4 × 𝑥𝑥 = 4 𝑥𝑥

29. Chhavi wants to fence in a rectangular
region to be used gardening. Its length
is 4 times the width. If the perimeter
of the rectangle is 180 feet, what are
the dimensions of the rectangle?
Step 4: Identify the relation
between known and unknown
• Known: ____________
• Unknown: ______, _______
• Relation:
________ = ____________________
Step 5: Use all values in the
equation
______ = ____________
⇒ 𝑥𝑥 = ?
Step 6: Find the unknowns

30. Chhavi wants to fence in a rectangular
region to be used gardening. Its length
is 4 times the width. If the perimeter
of the rectangle is 180 feet, what are
the dimensions of the rectangle?
Step 4: Identify the relation between
known and unknown
• Known: Perimeter
• Unknown: Width, Length
• Relation:
Perimeter = 2 × (Width + length)
Step 5: Use all values in the equation
180 = 2 × 𝑥𝑥 + 4𝑥𝑥
180 = 2 × 5𝑥𝑥
180 = 10𝑥𝑥
⇒ 𝑥𝑥 = 18
Step 6: Find the unknowns
Width = 𝑥𝑥 = 18 feet
Length = 4𝑥𝑥 = 4 × 18 = 72 feet

31. GIVE IT A TRY.
Komal wants to put a decorative border
around her kitchen. Her kitchen is
rectangular in shape and although she
does not remember the exact dimensions,
she does remember that the width of the
kitchen is 5 feet more than the length. If
the perimeter of the kitchen is 70 feet,
find the dimensions of her kitchen.

32. Komal wants to put a
decorative border around
her kitchen. Her kitchen is
rectangular in shape and
although she does not
remember the exact
dimensions, she does
remember that the width
of the kitchen is 5 feet
more than the length. If
the perimeter of the
kitchen is 70 feet, find the
dimensions of her kitchen.
Step 1: Identify what you are looking for
_________, ___________
Step 2: Identify the comparison statement
______________________
Step 3: Let the Independent and dependent
_________ = __________
_________ = __________

33. Step 4: Identify the relation between known and
unknown
• Known: ___________
• Unknown: ____________, ______________
• Relation:
__________ = ________________________
Step 5: Use all values in the equation
_______= _______________
⇒ 𝑥𝑥 = ?
Step 6: Find the unknowns
Komal wants to put a
decorative border around
her kitchen. Her kitchen is
rectangular in shape and
although she does not
remember the exact
dimensions, she does
remember that the width
of the kitchen is 5 feet
more than the length. If
the perimeter of the
kitchen is 70 feet, find the
dimensions of her kitchen.

34. PROBLEM - II
Drishti School organized a trip to Hardy’s
World Ludhiana. A Total of 180 students
who went for the journey . Two buses of
different capacity were booked for the
journey. One bus carried 14 more students
than the other. How many students did
each bus carry ?

35. Drishti School organized a
trip to Hardy’s World
Ludhiana. A Total of 180
students who went for the
journey . Two buses of
different capacity were
booked for the journey.
Bus A carried 13 more
students than Bus B. How
many students did each
bus carry ?
Step 1: Identify what you are looking for
_________, ___________
Step 2: Identify the comparison statement
______________________
Step 3: Let the Independent and dependent
_________ = __________
_________ = __________

36. Drishti School organized a
trip to Hardy’s World
Ludhiana. A Total of 180
students who went for the
journey . Two buses of
different capacity were
booked for the journey.
Bus A carried 13 more
students than Bus B. How
many students did each
bus carry ?
Step 1: Identify what you are looking for
Students in Bus A, Students in Bus B
Step 2: Identify the comparison statement
Bus A carried 14 more students than Bus B
Step 3: Let the Independent and dependent
Students in Bus B = 𝒙𝒙
Students in Bus A = 𝒙𝒙 + 14

37. Drishti School organized a
trip to Hardy’s World
Ludhiana. A Total of 180
students who went for the
journey . Two buses of
different capacity were
booked for the journey.
Bus A carried 13 more
students than Bus B. How
many students did each
bus carry ?
Step 4: Identify the relation between known and
unknown
• Known: ___________
• Unknown: ____________, ______________
• Relation:
__________ = ________________________
Step 5: Use all values in the equation
_______ = _____________
⇒ 𝑥𝑥 = ?
Step 6: Find the unknowns

38. Drishti School organized a
trip to Hardy’s World
Ludhiana. A Total of 180
students who went for the
journey . Two buses of
different capacity were
booked for the journey.
Bus A carried 13 more
students than Bus B. How
many students did each
bus carry ?
Step 4: Identify the relation between known and
unknown
• Known: Total Students
• Unknown: Students in Bus A, Students in Bus B
• Relation:
Total Students = Students in Bus A + Students in Bus B
Step 5: Use all values in the equation
180 = 𝑥𝑥 + 𝑥𝑥 + 14
⇒ 𝑥𝑥 = ?
Step 6: Find the unknowns

39. GIVE IT A TRY.
Udhey along with his family is
going for a trip to Shimla over the
course of 3 days. They plan on
traveling 200 km more on the
second day than they will on the
first day. They will travel 75 km less
on the third day than they will on
the first day. To total distance of
the trip is 1058 km. How many km
will they travel each day?

40. Step 1: Identify what you are looking for
_________, ___________
Step 2: Identify the comparison statement
______________________
Step 3: Let the Independent and dependent
_________ = __________
_________ = __________
Udhey along with his family
is going for a trip to Shimla
over the course of 3 days.
They plan on traveling 200
km more on the second day
than they will on the first
day. They will travel 75 km
less on the third day than
they will on the first day.
The total distance of the trip
is 1058 km. How many km
will they travel each day?

41. Step 4: Identify the relation between known and
unknown
• Known: ___________
• Unknown: ____________, ______________
• Relation:
__________ = ________________________
Step 5: Use all values in the equation
_______ = ______________
⇒ 𝑥𝑥 = ?
Step 6: Find the unknowns
Udhey along with his family
is going for a trip to Shimla
over the course of 3 days.
They plan on traveling 200
km more on the second day
than they will on the first
day. They will travel 75 km
less on the third day than
they will on the first day.
The total distance of the trip
is 1058 km. How many km
will they travel each day?

42. PROBLEM - III
Jotvir needed to cut a piece of
wood into two smaller
segments. The shorter piece
was 1 feet longer than half
the longer piece. If the length
of the entire piece of wood
was 7 feet, what is the length
of each piece?

43. Step 1: Identify what you are looking for
_________, ___________
Step 2: Identify the comparison statement
______________________
Step 3: Let the Independent and dependent
_________ = __________
_________ = __________
Jotvir needed to cut a piece
of wood into two smaller
segments. The shorter piece
was 1 feet longer than half
the longer piece. If the
length of the entire piece of
wood was 7 feet, what is the
length of each piece?

44. Step 1: Identify what you are looking for
length of the long piece , length of the short piece
Step 2: Identify the comparison statement
Shorter piece was 1 feet longer than half the longer
piece
Step 3: Let the Independent and dependent
length of the long piece = 𝒙𝒙
length of the short piece =
𝟏𝟏
𝟐𝟐
𝒙𝒙 + 𝟏𝟏
Jotvir needed to cut a piece
of wood into two smaller
segments. The shorter piece
was 1 feet longer than half
the longer piece. If the
length of the entire piece of
wood was 7 feet, what is the
length of each piece?

45. Step 4: Identify the relation between known and
unknown
• Known: ___________
• Unknown: ____________, ______________
• Relation:
__________ = ________________________
Step 5: Use all values in the equation
_______ = ______________
⇒ 𝑥𝑥 = ?
Step 6: Find the unknowns
Jotvir needed to cut a piece
of wood into two smaller
segments. The shorter piece
was 1 feet longer than half
the longer piece. If the
length of the entire piece of
wood was 7 feet, what is the
length of each piece?

46. Step 4: Identify the relation between known and
unknown
• Known: length of the entire piece
• Unknown: short piece, long piece
• Relation:
length of the entire piece = short piece + long piece
Step 5: Use all values in the equation
7 =
1
2
𝑥𝑥 + 1 + 𝑥𝑥
⇒ 𝑥𝑥 = ?
Step 6: Find the unknowns
Jotvir needed to cut a piece
of wood into two smaller
segments. The shorter piece
was 1 feet longer than half
the longer piece. If the
length of the entire piece of
wood was 7 feet, what is the
length of each piece?

47. GIVE IT A TRY.
Malvika needs to cut a piece of
fabric into two strips. The longer
piece needs to be 4 m longer
than twice the shorter piece. If
the length of the entire piece of
fabric is 10 m, what is the length
of each piece?