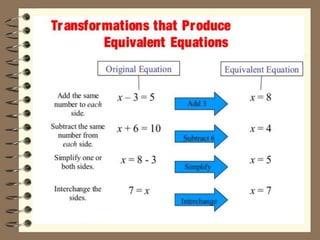
The document defines an equation as a condition of equality between two mathematical expressions. It provides examples of how to frame a simple equation using variables, coefficients, and constants. The key properties of equations are also outlined, such as how the left and right sides can be interchanged or terms can be added/subtracted/multiplied/divided if done to both sides. Examples are given to demonstrate solving equations using transposition or addition/subtraction/multiplication. Finally, word problems are presented and solved to find unknown values using simple equations.

1. Simple Equations
What is an Equation?
A condition of equality between two
mathematical expressions.

2. Framing an equation:
Example: Twice a number say x is added to
3 to get 7.
=> 2x + 3 = 7.
2 is the coefficient of x.
x is the variable.
3 and 7 are the constant terms.
(=) is the sign of equality.

3. Properties of an Equation.
The value of the variable for which the
equation is satisfied is called the solution of
the equation.
An equation remains the same if the L.H.S
and the R.H.S are interchanged.
In case of the balanced equation , if we add
subtract , multiply, divide both sides by the
same number, the balance remains
undisturbed i.e the value of L.H.S remains
equal to the value of R.H.S.

4. Solved example: addition.

5. Solved example:(subtraction
and division)

6. Solved example:
(subtraction & multiplication)

7. Transposition:
 The process of moving a term from one side of the
equation to the other side is called transposing. It is the
same as adding and subtracting a number from both sides
of the equation.
 Ex. Solve 5x + 9 = 19
 => Transposing 9 to the other side we get,
 => 5x = 19 – 9
 => 5x = 10
 Transposing 5 to the other side we get,
 x = 10/5
 x = 2
.

9. Word problems of simple
equation:
Q1.The denominator of a fraction exceeds the numerator by 5. If 3
be added to both, the fraction becomes 3/4. Find the fraction.
Solution :
Let "x" be the numerator.
"The denominator of the fraction exceeds the numerator"
From the above information,
Fraction = x / (x + 5) ----------(1)
"If 3 be added to both, the fraction becomes 3 / 4"
From the above information, we have
(x+3) / (x + 5 + 3) = 3 / 4

10.  Simplify.
 (x + 3) / (x + 8) = 3/4
 4(x + 3) = 3(x + 8)
 4x + 12 = 3x + 24
 x = 12
 Plug x = 12 in (1)
 Fraction = 12 / (12 + 5)
 Fraction = 12 / 17
 Hence, the required fraction is 12 / 17.

11.  Q2.If thrice of A's age 6 years ago be subtracted from twice his
present age, the result would be equal to his present age. Find A's
present age.
 Solution :
 Let "x" be A's present age.
 A's age 6 years ago = x - 6
 Thrice of A's age 6 years ago = 3(x-6)
 Twice his present age = 2x
 Given : Thrice of A's age 6 years ago be subtracted from twice his
present age, the result would be equal to his present age.
 So, we have
 2x - 3(x - 6) = x

12. Simplify.
2x - 3x + 18 = x
- x + 18 = x
18 = 2x
Divide both sides by 2.
9 = x
Hence, A's present age is 9 years.

13.  Q3.The fourth part of a number exceeds the sixth part by 4. Find
the number.
 Solution :
 Let "x" be the required number.
 Fourth part of the number = x/4
 Sixth part of the number = x/6
 Given : The fourth part of a number exceeds the sixth part by 4.
 x/4 - x/6 = 4
 L.C.M of (4, 6) is 12.
 (3x/12) - (2x/12) = 4
 .

14. Simplify.
(3x - 2x) / 12 = 4
x / 12 = 4
Multiply both sides by 12.
x = 48
Hence, the required number is 48.