This document presents an analysis of Java 7's dual pivot quicksort, highlighting its partitioning technique that utilizes two pivots instead of one. The comparison costs and effectiveness of the new algorithm are discussed, including its implementation details and benefits over the classic quicksort. The analysis draws from previous works and emphasizes the algorithm's performance and efficiency in sorting operations.

1. Average Case Analysis of
Java 7’s Dual Pivot Quicksort
Sebastian Wild Markus E. Nebel
[s_wild, nebel] @cs.uni-kl.de
Computer Science Department
University of Kaiserslautern
September 11, 2012
20th European Symposium on Algorithms
Sebastian Wild Java 7’s Dual Pivot Quicksort 2012/09/11 1 / 15

2. Classic Quicksort
Classic Quicksort with Hoare’s Crossing Pointer Technique
2 9 5 4 1 7 8 3 6
. . . by example
Sebastian Wild Java 7’s Dual Pivot Quicksort 2012/09/11 2 / 15

3. Classic Quicksort
Classic Quicksort with Hoare’s Crossing Pointer Technique
2 9 5 4 1 7 8 3 6
Select one element as pivot.
Sebastian Wild Java 7’s Dual Pivot Quicksort 2012/09/11 2 / 15

4. Classic Quicksort
Classic Quicksort with Hoare’s Crossing Pointer Technique
2 9 5 4 1 7 8 3 6
Only value relative to pivot counts.
Sebastian Wild Java 7’s Dual Pivot Quicksort 2012/09/11 2 / 15

5. Classic Quicksort
Classic Quicksort with Hoare’s Crossing Pointer Technique
2 9 5 4 1 7 8 3 6
Left pointer scans until first large element.
Sebastian Wild Java 7’s Dual Pivot Quicksort 2012/09/11 2 / 15

6. Classic Quicksort
Classic Quicksort with Hoare’s Crossing Pointer Technique
2 9 5 4 1 7 8 3 6
Right pointer scans until first small element.
Sebastian Wild Java 7’s Dual Pivot Quicksort 2012/09/11 2 / 15

7. Classic Quicksort
Classic Quicksort with Hoare’s Crossing Pointer Technique
2 9 5 4 1 7 8 3 6
Swap out-of-order pair.
Sebastian Wild Java 7’s Dual Pivot Quicksort 2012/09/11 2 / 15

8. Classic Quicksort
Classic Quicksort with Hoare’s Crossing Pointer Technique
2 3 5 4 1 7 8 9 6
Swap out-of-order pair.
Sebastian Wild Java 7’s Dual Pivot Quicksort 2012/09/11 2 / 15

9. Classic Quicksort
Classic Quicksort with Hoare’s Crossing Pointer Technique
2 3 5 4 1 7 8 9 6
Left pointer scans until first large element.
Sebastian Wild Java 7’s Dual Pivot Quicksort 2012/09/11 2 / 15

10. Classic Quicksort
Classic Quicksort with Hoare’s Crossing Pointer Technique
2 3 5 4 1 7 8 9 6
Right pointer scans until first small element.
Sebastian Wild Java 7’s Dual Pivot Quicksort 2012/09/11 2 / 15

11. Classic Quicksort
Classic Quicksort with Hoare’s Crossing Pointer Technique
2 3 5 4 1 7 8 9 6
The pointers have crossed!
Sebastian Wild Java 7’s Dual Pivot Quicksort 2012/09/11 2 / 15

12. Classic Quicksort
Classic Quicksort with Hoare’s Crossing Pointer Technique
2 3 5 4 1 7 8 9 6
Swap pivot to final position.
Sebastian Wild Java 7’s Dual Pivot Quicksort 2012/09/11 2 / 15

13. Classic Quicksort
Classic Quicksort with Hoare’s Crossing Pointer Technique
2 3 5 4 1 6 8 9 7
Partitioning done!
Sebastian Wild Java 7’s Dual Pivot Quicksort 2012/09/11 2 / 15

14. Classic Quicksort
Classic Quicksort with Hoare’s Crossing Pointer Technique
2 3 5 4 1 6 8 9 7
Recursively sort two sublists.
Sebastian Wild Java 7’s Dual Pivot Quicksort 2012/09/11 2 / 15

15. Classic Quicksort
Classic Quicksort with Hoare’s Crossing Pointer Technique
1 2 3 4 5 6 7 8 9
Done.
Sebastian Wild Java 7’s Dual Pivot Quicksort 2012/09/11 2 / 15

16. Dual Pivot Quicksort
“new” idea: use two pivots p < q
3 5 1 8 4 7 2 9 6
p q
How to do partitioning?
Sebastian Wild Java 7’s Dual Pivot Quicksort 2012/09/11 3 / 15

17. Dual Pivot Quicksort
“new” idea: use two pivots p < q
3 5 1 8 4 7 2 9 6
p q
How to do partitioning?
1 For each element x, determine its class
small for x < p
medium for p < x < q
large for q < x
by comparing x to p and/or q
2 Arrange elements according to classes p q
Sebastian Wild Java 7’s Dual Pivot Quicksort 2012/09/11 3 / 15

18. Dual Pivot Quicksort – Previous Work
Robert Sedgewick, 1975
in-place dual pivot Quicksort implementation
more comparisons and swaps than classic Quicksort
Pascal Hennequin, 1991
comparisons for list-based Quicksort with r pivots
r=2 same #comparisons as classic Quicksort
5
in one partitioning step: 3 comparisons per element
r>2 very small savings, but complicated partitioning
Sebastian Wild Java 7’s Dual Pivot Quicksort 2012/09/11 4 / 15

19. Dual Pivot Quicksort – Previous Work
Robert Sedgewick, 1975
in-place dual pivot Quicksort implementation
more comparisons and swaps than classic Quicksort
Pascal Hennequin, 1991
comparisons for list-based Quicksort with r pivots
r=2 same #comparisons as classic Quicksort
5
in one partitioning step: 3 comparisons per element
r>2 very small savings, but complicated partitioning
Using two pivots does not pay.
Sebastian Wild Java 7’s Dual Pivot Quicksort 2012/09/11 4 / 15

20. Dual Pivot Quicksort – Previous Work
Robert Sedgewick, 1975
in-place dual pivot Quicksort implementation
more comparisons and swaps than classic Quicksort
Pascal Hennequin, 1991
comparisons for list-based Quicksort with r pivots
r=2 same #comparisons as classic Quicksort
5
in one partitioning step: 3 comparisons per element
r>2 very small savings, but complicated partitioning
Using two pivots does not pay.
Vladimir Yaroslavskiy, 2009
new implementation of dual pivot Quicksort
now used in Java 7’s runtime library
runtime studies, no rigorous analysis
Sebastian Wild Java 7’s Dual Pivot Quicksort 2012/09/11 4 / 15

21. Dual Pivot Quicksort – Comparison Costs
How many comparisons to determine classes ( small , medium or large ) ?
Assume, we first compare with p.
small elements need 1, others 2 comparisons
on average: 1 of all elements are small
3
1 2 5
3 · 1 + 3 · 2 = 3 comparisons per element
if inputs are uniform random permutations,
classes of x and y are independent
Any partitioning method needs at least
5 20
3 (n − 2) ∼ 12 n comparisons on average?
Sebastian Wild Java 7’s Dual Pivot Quicksort 2012/09/11 5 / 15

22. Dual Pivot Quicksort – Comparison Costs
How many comparisons to determine classes ( small , medium or large ) ?
Assume, we first compare with p.
small elements need 1, others 2 comparisons
on average: 1 of all elements are small
3
1 2 5
3 · 1 + 3 · 2 = 3 comparisons per element
if inputs are uniform random permutations,
classes of x and y are independent
Any partitioning method needs at least
5 20
3 (n − 2) ∼ 12 n comparisons on average?
No! (Stay tuned . . . )
Sebastian Wild Java 7’s Dual Pivot Quicksort 2012/09/11 5 / 15

23. Beating the “Lower Bound”
∼ 20 n comparisons only needed,
12
if there is one comparison location,
then checks for x and y independent
But: Can have several comparison locations!
Here: Assume two locations C1 and C2 s. t.
C1 first compares with p. C1 executed often, iff p is large.
C2 first compares with q. C2 executed often, iff q is small.
C1 executed often
iff many small elements
iff good chance that C1 needs only one comparison
(C2 similar)
5
less comparisons than 3 per elements on average
Sebastian Wild Java 7’s Dual Pivot Quicksort 2012/09/11 6 / 15

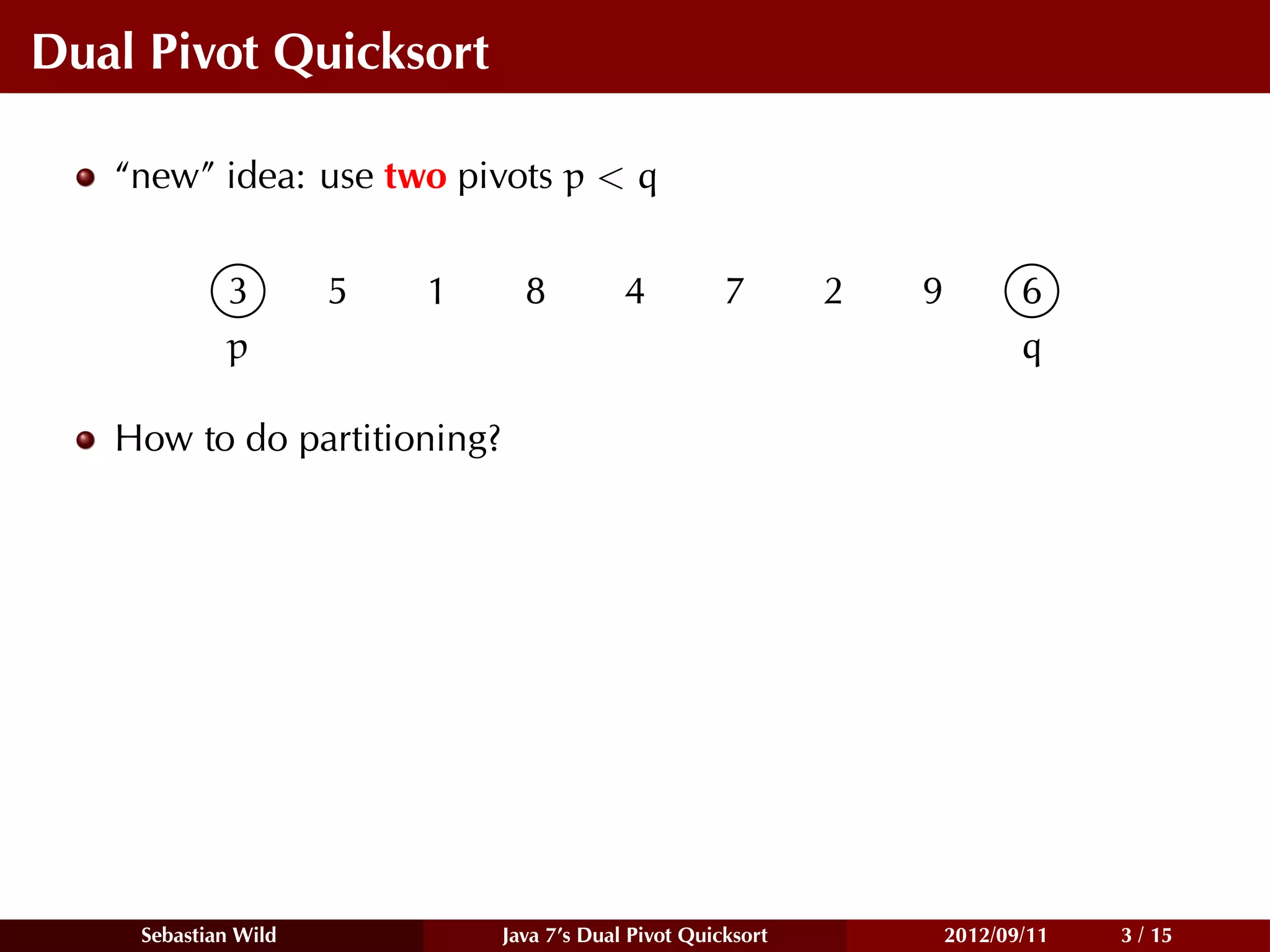
24. Yaroslavskiy’s Quicksort – Example
Yaroslavskiy’s Dual Pivot Quicksort
(used in Oracle’s Java 7 Arrays.sort(int[]))
p q
3 5 1 8 4 7 2 9 6
Select two elements as pivots.
Invariant: <p p ◦ q k ? g >q
→ → ←
Sebastian Wild Java 7’s Dual Pivot Quicksort 2012/09/11 7 / 15

25. Yaroslavskiy’s Quicksort – Example
Yaroslavskiy’s Dual Pivot Quicksort
(used in Oracle’s Java 7 Arrays.sort(int[]))
p q
3 5 1 8 4 7 2 9 6
Only value relative to pivot counts.
Invariant: <p p ◦ q k ? g >q
→ → ←
Sebastian Wild Java 7’s Dual Pivot Quicksort 2012/09/11 7 / 15

26. Yaroslavskiy’s Quicksort – Example
Yaroslavskiy’s Dual Pivot Quicksort
(used in Oracle’s Java 7 Arrays.sort(int[]))
k
3 5 1 8 4 7 2 9 6
A[k] is medium go on
Invariant: <p p ◦ q k ? g >q
→ → ←
Sebastian Wild Java 7’s Dual Pivot Quicksort 2012/09/11 7 / 15

27. Yaroslavskiy’s Quicksort – Example
Yaroslavskiy’s Dual Pivot Quicksort
(used in Oracle’s Java 7 Arrays.sort(int[]))
k
3 5 1 8 4 7 2 9 6
A[k] is small Swap to left
Invariant: <p p ◦ q k ? g >q
→ → ←
Sebastian Wild Java 7’s Dual Pivot Quicksort 2012/09/11 7 / 15

28. Yaroslavskiy’s Quicksort – Example
Yaroslavskiy’s Dual Pivot Quicksort
(used in Oracle’s Java 7 Arrays.sort(int[]))
k
3 5 1 8 4 7 2 9 6
Swap small element to left end.
Invariant: <p p ◦ q k ? g >q
→ → ←
Sebastian Wild Java 7’s Dual Pivot Quicksort 2012/09/11 7 / 15

29. Yaroslavskiy’s Quicksort – Example
Yaroslavskiy’s Dual Pivot Quicksort
(used in Oracle’s Java 7 Arrays.sort(int[]))
k
3 1 5 8 4 7 2 9 6
Swap small element to left end.
Invariant: <p p ◦ q k ? g >q
→ → ←
Sebastian Wild Java 7’s Dual Pivot Quicksort 2012/09/11 7 / 15

30. Yaroslavskiy’s Quicksort – Example
Yaroslavskiy’s Dual Pivot Quicksort
(used in Oracle’s Java 7 Arrays.sort(int[]))
k
3 1 5 8 4 7 2 9 6
A[k] is large Find swap partner.
Invariant: <p p ◦ q k ? g >q
→ → ←
Sebastian Wild Java 7’s Dual Pivot Quicksort 2012/09/11 7 / 15

31. Yaroslavskiy’s Quicksort – Example
Yaroslavskiy’s Dual Pivot Quicksort
(used in Oracle’s Java 7 Arrays.sort(int[]))
k g
3 1 5 8 4 7 2 9 6
A[k] is large Find swap partner:
g skips over large elements.
Invariant: <p p ◦ q k ? g >q
→ → ←
Sebastian Wild Java 7’s Dual Pivot Quicksort 2012/09/11 7 / 15

32. Yaroslavskiy’s Quicksort – Example
Yaroslavskiy’s Dual Pivot Quicksort
(used in Oracle’s Java 7 Arrays.sort(int[]))
k g
3 1 5 8 4 7 2 9 6
A[k] is large Swap
Invariant: <p p ◦ q k ? g >q
→ → ←
Sebastian Wild Java 7’s Dual Pivot Quicksort 2012/09/11 7 / 15

33. Yaroslavskiy’s Quicksort – Example
Yaroslavskiy’s Dual Pivot Quicksort
(used in Oracle’s Java 7 Arrays.sort(int[]))
k g
3 1 5 2 4 7 8 9 6
A[k] is large Swap
Invariant: <p p ◦ q k ? g >q
→ → ←
Sebastian Wild Java 7’s Dual Pivot Quicksort 2012/09/11 7 / 15

34. Yaroslavskiy’s Quicksort – Example
Yaroslavskiy’s Dual Pivot Quicksort
(used in Oracle’s Java 7 Arrays.sort(int[]))
k g
3 1 5 2 4 7 8 9 6
A[k] is old A[g], small Swap to left
Invariant: <p p ◦ q k ? g >q
→ → ←
Sebastian Wild Java 7’s Dual Pivot Quicksort 2012/09/11 7 / 15

35. Yaroslavskiy’s Quicksort – Example
Yaroslavskiy’s Dual Pivot Quicksort
(used in Oracle’s Java 7 Arrays.sort(int[]))
k g
3 1 2 5 4 7 8 9 6
A[k] is old A[g], small Swap to left
Invariant: <p p ◦ q k ? g >q
→ → ←
Sebastian Wild Java 7’s Dual Pivot Quicksort 2012/09/11 7 / 15

36. Yaroslavskiy’s Quicksort – Example
Yaroslavskiy’s Dual Pivot Quicksort
(used in Oracle’s Java 7 Arrays.sort(int[]))
k g
3 1 2 5 4 7 8 9 6
A[k] is medium go on
Invariant: <p p ◦ q k ? g >q
→ → ←
Sebastian Wild Java 7’s Dual Pivot Quicksort 2012/09/11 7 / 15

37. Yaroslavskiy’s Quicksort – Example
Yaroslavskiy’s Dual Pivot Quicksort
(used in Oracle’s Java 7 Arrays.sort(int[]))
k g
3 1 2 5 4 7 8 9 6
A[k] is large Find swap partner.
Invariant: <p p ◦ q k ? g >q
→ → ←
Sebastian Wild Java 7’s Dual Pivot Quicksort 2012/09/11 7 / 15

38. Yaroslavskiy’s Quicksort – Example
Yaroslavskiy’s Dual Pivot Quicksort
(used in Oracle’s Java 7 Arrays.sort(int[]))
g k
3 1 2 5 4 7 8 9 6
A[k] is large Find swap partner:
g skips over large elements.
Invariant: <p p ◦ q k ? g >q
→ → ←
Sebastian Wild Java 7’s Dual Pivot Quicksort 2012/09/11 7 / 15

39. Yaroslavskiy’s Quicksort – Example
Yaroslavskiy’s Dual Pivot Quicksort
(used in Oracle’s Java 7 Arrays.sort(int[]))
g k
3 1 2 5 4 7 8 9 6
g and k have crossed!
Swap pivots in place
Invariant: <p p ◦ q k ? g >q
→ → ←
Sebastian Wild Java 7’s Dual Pivot Quicksort 2012/09/11 7 / 15

40. Yaroslavskiy’s Quicksort – Example
Yaroslavskiy’s Dual Pivot Quicksort
(used in Oracle’s Java 7 Arrays.sort(int[]))
g k
2 1 3 5 4 6 8 9 7
g and k have crossed!
Swap pivots in place
Invariant: <p p ◦ q k ? g >q
→ → ←
Sebastian Wild Java 7’s Dual Pivot Quicksort 2012/09/11 7 / 15

41. Yaroslavskiy’s Quicksort – Example
Yaroslavskiy’s Dual Pivot Quicksort
(used in Oracle’s Java 7 Arrays.sort(int[]))
2 1 3 5 4 6 8 9 7
Partitioning done!
Invariant: <p p ◦ q k ? g >q
→ → ←
Sebastian Wild Java 7’s Dual Pivot Quicksort 2012/09/11 7 / 15

42. Yaroslavskiy’s Quicksort – Example
Yaroslavskiy’s Dual Pivot Quicksort
(used in Oracle’s Java 7 Arrays.sort(int[]))
2 1 3 5 4 6 8 9 7
Recursively sort three sublists.
Invariant: <p p ◦ q k ? g >q
→ → ←
Sebastian Wild Java 7’s Dual Pivot Quicksort 2012/09/11 7 / 15

43. Yaroslavskiy’s Quicksort – Example
Yaroslavskiy’s Dual Pivot Quicksort
(used in Oracle’s Java 7 Arrays.sort(int[]))
1 2 3 4 5 6 7 8 9
Done.
Invariant: <p p ◦ q k ? g >q
→ → ←
Sebastian Wild Java 7’s Dual Pivot Quicksort 2012/09/11 7 / 15

44. Yaroslavskiy’s Quicksort
DUALPIVOTQUICKSORT YAROSLAVSKIY(A, left, right)
1 if right − left 1
2 p := A[left]; q := A[right]
3 if p > q then Swap p and q end if
4 := left + 1; g := right − 1; k :=
5 while k g
6 if A[k] < p
7 Swap A[k] and A[ ] ; := + 1
8 else if A[k] q
9 while A[g] > q and k < g do g := g − 1 end while
10 Swap A[k] and A[g] ; g := g − 1
11 if A[k] < p
12 Swap A[k] and A[ ] ; := + 1
13 end if
14 end if
15 k := k + 1
16 end while
17 := − 1; g := g + 1
18 Swap A[left] and A[ ] ; Swap A[right] and A[g]
19 DUALPIVOTQUICKSORT YAROSLAVSKIY(A, left , − 1 )
20 DUALPIVOTQUICKSORT YAROSLAVSKIY(A, + 1 , g − 1)
21 DUALPIVOTQUICKSORT YAROSLAVSKIY(A, g + 1, right )
22 end if
Sebastian Wild Java 7’s Dual Pivot Quicksort 2012/09/11 8 / 15

45. Yaroslavskiy’s Quicksort
DUALPIVOTQUICKSORT YAROSLAVSKIY(A, left, right)
1 if right − left 1
2 p := A[left]; q := A[right] 2 comparison locations
3 if p > q then Swap p and q end if
4 := left + 1; g := right − 1; k := Ck handles pointer k
5 while k g
6 Ck if A[k] < p Cg handles pointer g
7 Swap A[k] and A[ ] ; := + 1
8 Ck else if A[k] q
9 Cg while A[g] > q and k < g do g := g − 1 end while
10 Swap A[k] and A[g] ; g := g − 1
11 Cg if A[k] < p
12 Swap A[k] and A[ ] ; := + 1
13 end if Ck first checks < p
14 end if Ck if needed q
15 k := k + 1
16 end while
Cg first checks > q
17 := − 1; g := g + 1
18 Swap A[left] and A[ ] ; Swap A[right] and A[g] Cg if needed < p
19 DUALPIVOTQUICKSORT YAROSLAVSKIY(A, left , − 1 )
20 DUALPIVOTQUICKSORT YAROSLAVSKIY(A, + 1 , g − 1)
21 DUALPIVOTQUICKSORT YAROSLAVSKIY(A, g + 1, right )
22 end if
Sebastian Wild Java 7’s Dual Pivot Quicksort 2012/09/11 8 / 15

46. Analysis of Yaroslavskiy’s Algorithm
In this talk:

only number of comparisons (swaps similar) 
all exact results
only leading term asymptotics
 in the paper
some marginal cases excluded
Cn expected #comparisons to sort random permutation of {1, . . . , n}
Cn satisfies recurrence relation
2
C n = cn + n(n−1) Cp−1 + Cq−p−1 + Cn−q ,
1 p<q n
with cn expected #comparisons in first partitioning step
recurrence solvable by standard methods
6
linear cn ∼ a · n yields Cn ∼ 5 a · n ln n.
need to compute cn
Sebastian Wild Java 7’s Dual Pivot Quicksort 2012/09/11 9 / 15

47. Analysis of Yaroslavskiy’s Algorithm
first comparison for all elements (at Ck or Cg )
∼ n comparisons
second comparison for some elements at Ck resp. Cg
. . . but how often are Ck resp. Cg reached?
Ck : all non- small elements reached by pointer k.
Cg : all non- large elements reached by pointer g.
second comparison for medium elements not avoidable
1
∼ 3 n comparisons in expectation
it remains to count:
large elements reached by k and
small elements reached by g.
Sebastian Wild Java 7’s Dual Pivot Quicksort 2012/09/11 10 / 15

48. Analysis of Yaroslavskiy’s Algorithm
Second comparisons for small and large elements?
Depends on location!
Ck l @ K: number of large elements at positions K.
Cg s @ G: number of small elements at positions G.
Recall invariant: <p p ◦ q k ? g >q
→ → ←
k and g cross at (rank of) q
l@K = 3 s@G = 2
p q
positions K = {2, . . . , q − 1} G = {q, . . . , n − 1}
for given p and q, l @ K hypergeometrically distributed
q−2
E [l @ K | p, q] = (n − q) n−2
Sebastian Wild Java 7’s Dual Pivot Quicksort 2012/09/11 11 / 15

49. Analysis of Yaroslavskiy’s Algorithm
law of total expectation:
q−2
E [l @ K] = Pr[pivots (p, q)] · (n − q) n−2 ∼ 1
6n
1 p<q n
Similarly: E [s @ G] ∼ 1
12 n.
Summing up contributions:
cn ∼ n first comparisons
1
+ 3n medium elements
1
+ 6n large elements at Ck
1
+ 12 n small elements at Cg
19
= 12 n
20
Recall: “lower bound” was 12 n.
Sebastian Wild Java 7’s Dual Pivot Quicksort 2012/09/11 12 / 15

50. Results
Comparisons:
6 19
Yaroslavskiy needs ∼ 5 · 12 n ln n = 1.9 n ln n on average.
Classic Quicksort needs ∼ 2 n ln n comparisons!
Swaps:
∼ 0.6 n ln n swaps for Yaroslavskiy’s algorithm vs.
∼ 0.3 n ln n swaps for classic Quicksort
Sebastian Wild Java 7’s Dual Pivot Quicksort 2012/09/11 13 / 15

51. Summary
We can exploit asymmetries to save comparisons!
Many extra swaps might hurt.
However, runtime studies favor dual pivot Quicksort:
more than 10 % faster!
Classic Quicksort
8 Yaroslavskiy
10−6 · n ln n
time
7.5
Normalized Java runtimes (in ms).
Average and standard deviation
7 of 1000 random permutations
per size.
0 0.5 1 1.5 2
n ·106
Sebastian Wild Java 7’s Dual Pivot Quicksort 2012/09/11 14 / 15

52. Open Questions
Closer look at runtime: Why is Yaroslavskiy so fast in practice?
experimental studies?
Input distributions other than random permutations
equal elements
presorted lists
Variances of Costs, Limiting Distributions?
Sebastian Wild Java 7’s Dual Pivot Quicksort 2012/09/11 15 / 15

53. Lower Bound on Comparisons
How clever can dual pivot paritioning be?
For lower bound, assume
random permutation model
pivots are selected uniformly
an oracle tells us, whether more small or more large elements occur
1 comparison for frequent extreme elements
2 comparisons for middle and rare extreme elements
2
(n − 2) + n(n−1) (q − p − 1) + min{p − 1, n − q}
1 p<q n
3 18
∼ 2n = 12 n
Even with unrealistic oracle, not much better than Yaroslavskiy
Sebastian Wild Java 7’s Dual Pivot Quicksort 2012/09/11 16 / 15

54. Counting Primitive Instructions à la Knuth
for implementations MMIX and Java bytecode
determine exact expected overall costs
MMIX: processor cycles “oops” υ and memory accesses “mems” µ
Bytecode: #executed instructions
divide program code into basic blocks
count cost contribution for blocks
determine expected execution frequencies of blocks
in first partitioning step
total frequency via recurrence relation
Sebastian Wild Java 7’s Dual Pivot Quicksort 2012/09/11 17 / 15

55. Counting Primitive Instructions à la Knuth
Results:
Algorithm total expected costs
MMIX Classic (11υ+2.6µ)(n+1)Hn +(11υ+3.7µ)n+(−11.5υ−4.5µ)
(13.1υ+2.8µ)(n + 1)Hn + (−1.695υ + 1.24µ)n
MMIX Yaroslavskiy
+ (−1.6783υ − 1.793µ)
Bytecode Classic 18(n + 1)Hn + 2n − 15
Bytecode
23.8(n + 1)Hn − 8.71n − 4.743
Yaroslavskiy
Classic Quicksort significantly better in both measures . . .
Why is Yaroslavskiy faster in practice?
Sebastian Wild Java 7’s Dual Pivot Quicksort 2012/09/11 18 / 15

56. Pivot Sampling
Idea: choose pivots from random sample of list
median for classic Quicksort
tertiles for dual pivot Quicksort
Sebastian Wild Java 7’s Dual Pivot Quicksort 2012/09/11 19 / 15

57. Pivot Sampling
Idea: choose pivots from random sample of list
median for classic Quicksort
tertiles for dual pivot Quicksort?
or asymmetric order statistics?
Here: sample of constant size k
choose pivots, such that t1 elements < p,
t2 elements between p and q,
t3 = k − 2 − t1 − t2 larger > q
Allows to “push” pivot towards desired order statistic of list
Sebastian Wild Java 7’s Dual Pivot Quicksort 2012/09/11 19 / 15

58. Pivot Sampling
leading n ln n term coefficient of
Comparisons for k = 11
tertiles
(t1 , t2 , t3 ) = (3, 3, 3)
∼ 1.609 n ln n
minimum
(t1 , t2 , t3 ) = (4, 2, 3)
∼ 1.585 n ln n
asymmetric order
statistics are better!
Sebastian Wild Java 7’s Dual Pivot Quicksort 2012/09/11 20 / 15