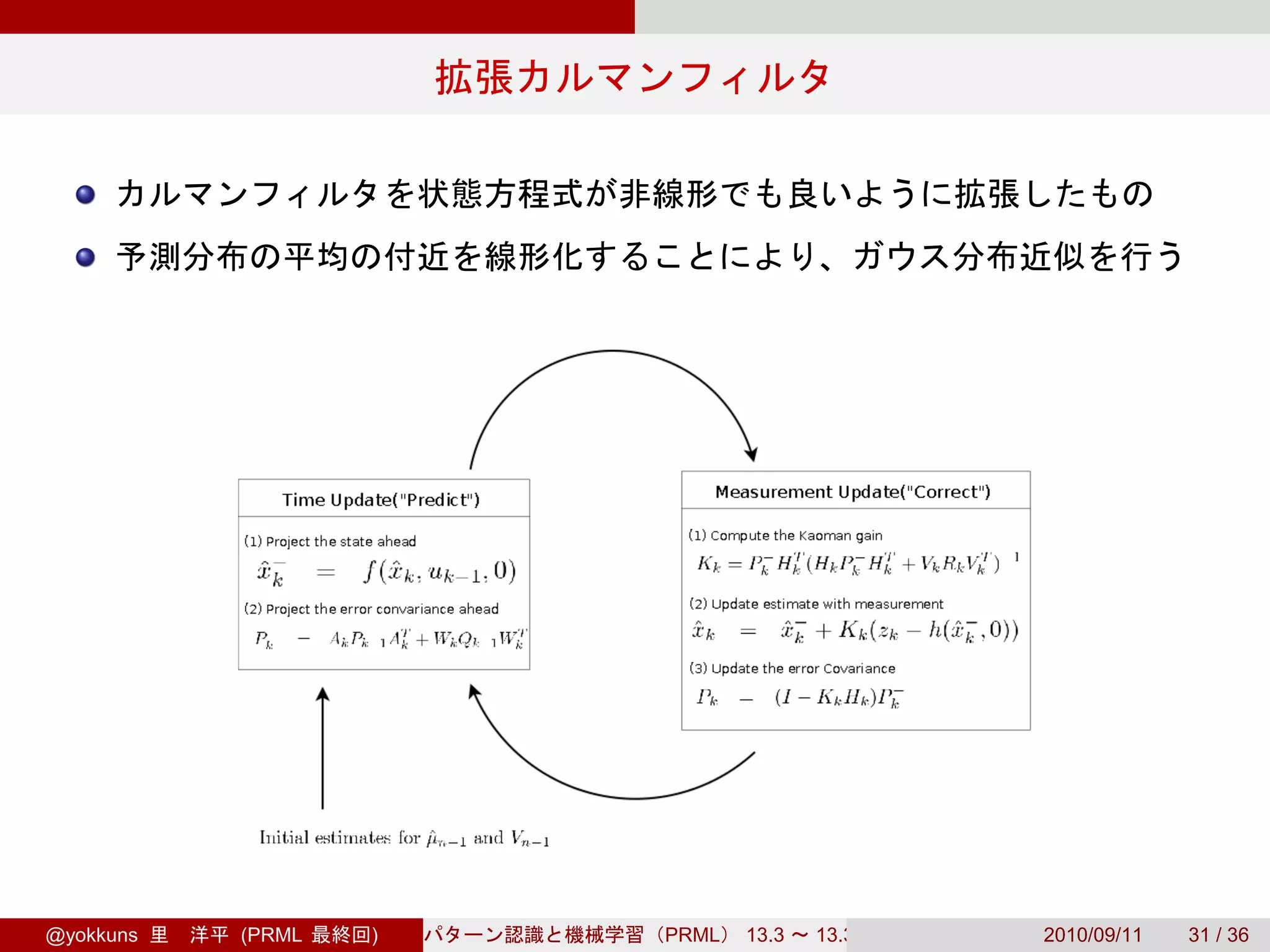
The document discusses linear dynamical systems (LDS) and their applications. It covers the basic LDS model and equations, parameter estimation using expectation-maximization (EM), and future event announcements for discussing LDS including a meeting of the Tokyo R user group on September 19. The summary is provided in 3 sentences or less as requested.

1. PRML
13.3 13.3.3
.
@yokkuns
.
PRML
2010/09/11
@yokkuns (PRML ) PRML 13.3 13.3.3 2010/09/11 1 / 36

2. PRML 13.3 13.3.3
@yokkuns (PRML ) PRML 13.3 13.3.3 2010/09/11 2 / 36

3. AGENDA
Linear Dynamical System
LDS
LDS
LDS
@yokkuns (PRML ) PRML 13.3 13.3.3 2010/09/11 3 / 36

4. AGENDA
Linear Dynamical System
LDS
LDS
LDS
@yokkuns (PRML ) PRML 13.3 13.3.3 2010/09/11 4 / 36

5. ID : yokkuns
:
: Web
http://twitter.com/yokkuns
@yokkuns (PRML ) PRML 13.3 13.3.3 2010/09/11 5 / 36

6. - 1
R Tokyo.R
http://groups.google.co.jp/group/r-study-tokyo
@yokkuns (PRML ) PRML 13.3 13.3.3 2010/09/11 6 / 36

7. - 2
PRML
http://groups.google.co.jp/group/grinning-math
@yokkuns (PRML ) PRML 13.3 13.3.3 2010/09/11 7 / 36

8. -
PRML
2010.09.11 RPML 13.3 13.3.3
9 R R II
2010.09.19
Tokyo.R#09 4
7
2010.09.25 +WEB
Tokyo.Webmining#7
@yokkuns (PRML ) PRML 13.3 13.3.3 2010/09/11 8 / 36

9. -
PRML
2010.09.11 RPML 13.3 13.3.3
9 R R II
2010.09.19
Tokyo.R#09 4
7
2010.09.25 +WEB
Tokyo.Webmining#7
@yokkuns (PRML ) PRML 13.3 13.3.3 2010/09/11 9 / 36

10. AGENDA
Linear Dynamical System
LDS
LDS
LDS
@yokkuns (PRML ) PRML 13.3 13.3.3 2010/09/11 10 / 36

11. @yokkuns (PRML ) PRML 13.3 13.3.3 2010/09/11 11 / 36

12. PCA
@yokkuns (PRML ) PRML 13.3 13.3.3 2010/09/11 12 / 36

13. p(z n|z n−1 ) = N(z n| Az n−1 , γ)
p(x n|z n) = N(x n|Cz n, σ)
p(z1 ) = N(z1 |µ0 , P0 )
@yokkuns (PRML ) PRML 13.3 13.3.3 2010/09/11 13 / 36

14. -
zn = Az n−1 + w n
x n = Cz n + v n
z 1 = µ0 + u
w ∼ N(x|0, Γ)
v ∼ N(v|0, Σ)
u ∼ N(u|0, V0 )
@yokkuns (PRML ) PRML 13.3 13.3.3 2010/09/11 14 / 36

15. x1:n
zn
zn
@yokkuns (PRML ) PRML 13.3 13.3.3 2010/09/11 15 / 36

16. zn
α
β
@yokkuns (PRML ) PRML 13.3 13.3.3 2010/09/11 16 / 36

17. AGENDA
Linear Dynamical System
LDS
LDS
LDS
@yokkuns (PRML ) PRML 13.3 13.3.3 2010/09/11 17 / 36

18. @yokkuns (PRML ) PRML 13.3 13.3.3 2010/09/11 18 / 36

19. p(z n|x1 , ..., x n)
α(z n) = N(z n|µ n, V n)
ˆ
(13.59)
∫
c nα(z n) =
ˆ p(x n|z n) α(z n−1 ) p(z n|z n−1 )dz n−1
ˆ
@yokkuns (PRML ) PRML 13.3 13.3.3 2010/09/11 19 / 36

20. (13.75) (13.76)
∫
c nN(z n|µ n, V n) = N(x n|Cz n, Σ) N(z n| Az n−1 , Γ)N(z n−1 |µ n−1 , V n−1 )dz n−1
(2.115)
∫
N(z n| Az n−1 , Γ)N(z n−1 |µ n−1 , V n−1 )dz n−1 = N(z n| Aµ n−1 , AV n−1 AT + Γ)
@yokkuns (PRML ) PRML 13.3 13.3.3 2010/09/11 20 / 36

21. (2.115) (2.116)
P n−1 = AV n−1 AT + Γ
µn = Aµ n−1 + K n(x n − C Aµ n−1 )
V n = (I − K nC)P n−1
K n = P n−1 CT (CP n−1 CT + Σ)−1
@yokkuns (PRML ) PRML 13.3 13.3.3 2010/09/11 21 / 36

22. @yokkuns (PRML ) PRML 13.3 13.3.3 2010/09/11 22 / 36

23. LDS β(z n)
ˆ
γ(z n) = α(z n)β(z n)
ˆ ˆ
γ(z n)
γ(z n) = N(z n|µ n, V n)
ˆ ˆ
∫
c n+1 β(z n) =
ˆ β(z n+1 )p(x n+1 |z n+1 )p(z n+1 |z n)dz n+1
ˆ
@yokkuns (PRML ) PRML 13.3 13.3.3 2010/09/11 23 / 36

24. µ n, V n
ˆ ˆ J n = V n AT (P n)−1
µ n = µ n + J n(µ n+1 − Aµ n)
ˆ ˆ
Vˆn = V n + J n(V n+1 − P n)J T
ˆ
n
µn Vn
@yokkuns (PRML ) PRML 13.3 13.3.3 2010/09/11 24 / 36

25. EM 2
(13.65)
ζ(z n−1 , z n) = (c n)−1 α(z n−1 )p(x n|z n)p(z n|z n−1 )β(z n)
ˆ ˆ
N(z n−1 |µ n−1 , V n−1 )N(z n|Az n−1 , Γ)N(x n|Cz n, Σ)N(z n|µ n, V n)
ˆ ˆ
=
c nα(z n)
ˆ
(13.84) α(z n)
ˆ ζ(z n−1 , z n)
[µ n−1 , µ n]T
ˆ ˆ
zn z n−1
cov[z n−1 , z n] = ˆ
J n−1 V n
@yokkuns (PRML ) PRML 13.3 13.3.3 2010/09/11 25 / 36

26. AGENDA
Linear Dynamical System
LDS
LDS
LDS
@yokkuns (PRML ) PRML 13.3 13.3.3 2010/09/11 26 / 36

27. LDS -
θ = { A, Γ, C, Σ, µ0 , V0 }
EM
θ old
p(Z|X, θ old )
(13.104)
E[z n] = µn
ˆ
E[z n zT ]
n−1
= J n−1 V n + µ nµT
ˆ ˆ ˆ n−1
E[z n zT ]
n = V n + µ nµT
ˆ ˆ ˆn
@yokkuns (PRML ) PRML 13.3 13.3.3 2010/09/11 27 / 36

28. LDS -
(13.6)
∑
N
ln p(X, Z|θ) = ln p(z1 |µ0 , V0 ) + ln p(z n|z n−1 , A, Γ)
n=2
∑
N
+ ln p(x n|z n, C, Σ)
n=1
p(Z|X, θ old )
Q(θ, θ old ) = E Z|θ old [ln p(X, Z|θ)]
θ = {A, Γ, C, Σ, µ0 , V0 }
@yokkuns (PRML ) PRML 13.3 13.3.3 2010/09/11 28 / 36

29. LDS -
µ0
new
= E[z1 ]
new
V0 = E[z1 zT ] − E[z1 ]E[z1T ]
1
 N  N −1
∑

  ∑

 


A new = 

 E[z n zT ] 

 E[z n−1 zT ]

 n−1   n 
n=2 n=2
1 ∑{
N
Γ new = E[z n zT ] − A new E[z n−1 zT ]
n n
N−1 n=2
}
−E[z n zT ]( A new )T + A new E[z n−1 zT ]( A new )T
n−1 n−1
 N  N −1
∑

  ∑

 


C new = 

 x n E[zT ] 
 E[z n zT ]

 n 
 n 
n=1 n=1
1 ∑{
N
Σ new = x n xT − (C new )T E[z n]xT
n n
N n=1
}
−x n E[zT ]C new + (C new )T E[z n zT ]C new
n n
@yokkuns (PRML ) PRML 13.3 13.3.3 2010/09/11 29 / 36

30. AGENDA
Linear Dynamical System
LDS
LDS
LDS
@yokkuns (PRML ) PRML 13.3 13.3.3 2010/09/11 30 / 36

31. @yokkuns (PRML ) PRML 13.3 13.3.3 2010/09/11 31 / 36

32. 1
1
@yokkuns (PRML ) PRML 13.3 13.3.3 2010/09/11 32 / 36

33. AGENDA
Linear Dynamical System
LDS
LDS
LDS
@yokkuns (PRML ) PRML 13.3 13.3.3 2010/09/11 33 / 36

34. 9/19( ) 9 R
@yokkuns (PRML ) PRML 13.3 13.3.3 2010/09/11 34 / 36

35. AGENDA
Linear Dynamical System
LDS
LDS
LDS
@yokkuns (PRML ) PRML 13.3 13.3.3 2010/09/11 35 / 36

36. @yokkuns (PRML ) PRML 13.3 13.3.3 2010/09/11 36 / 36