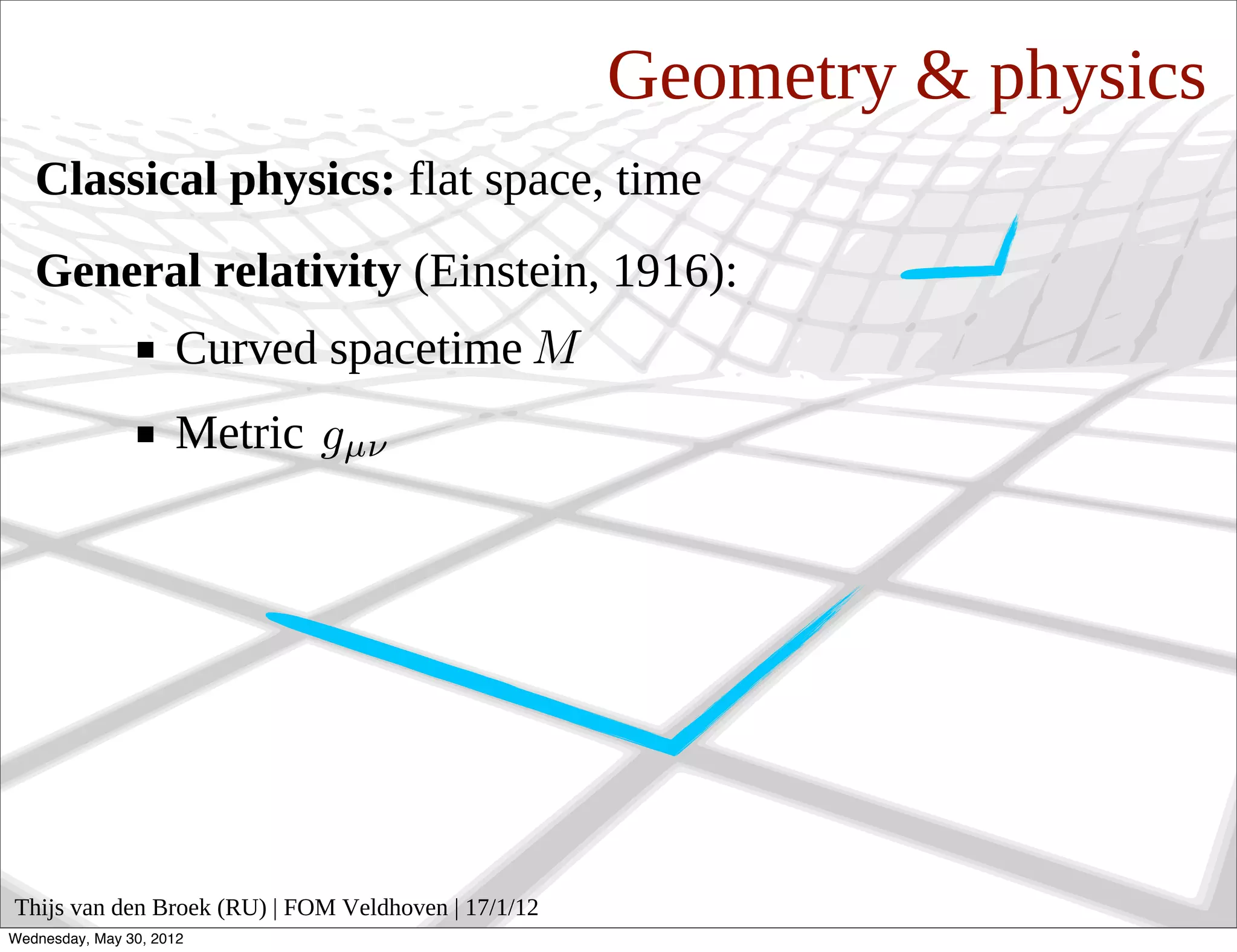
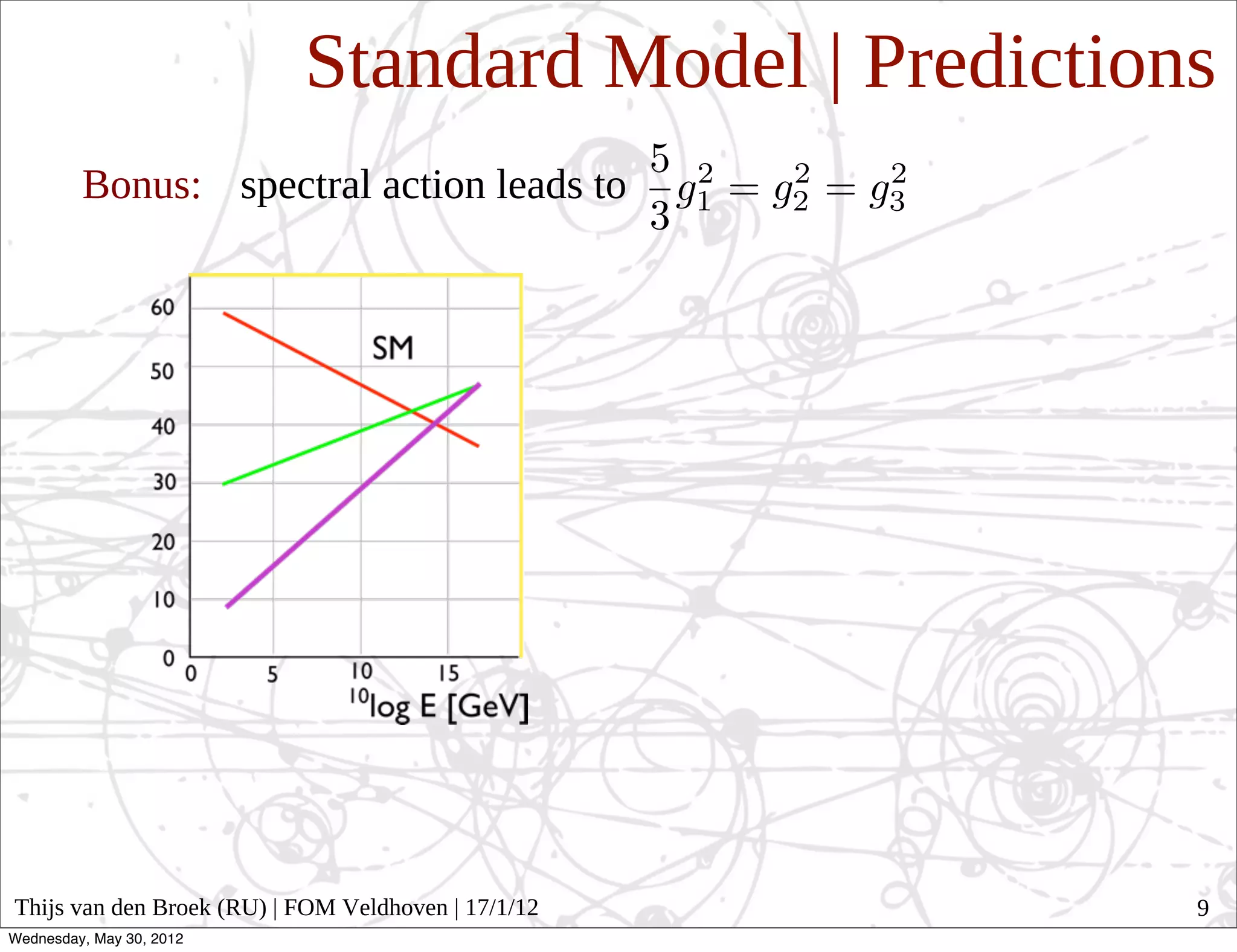
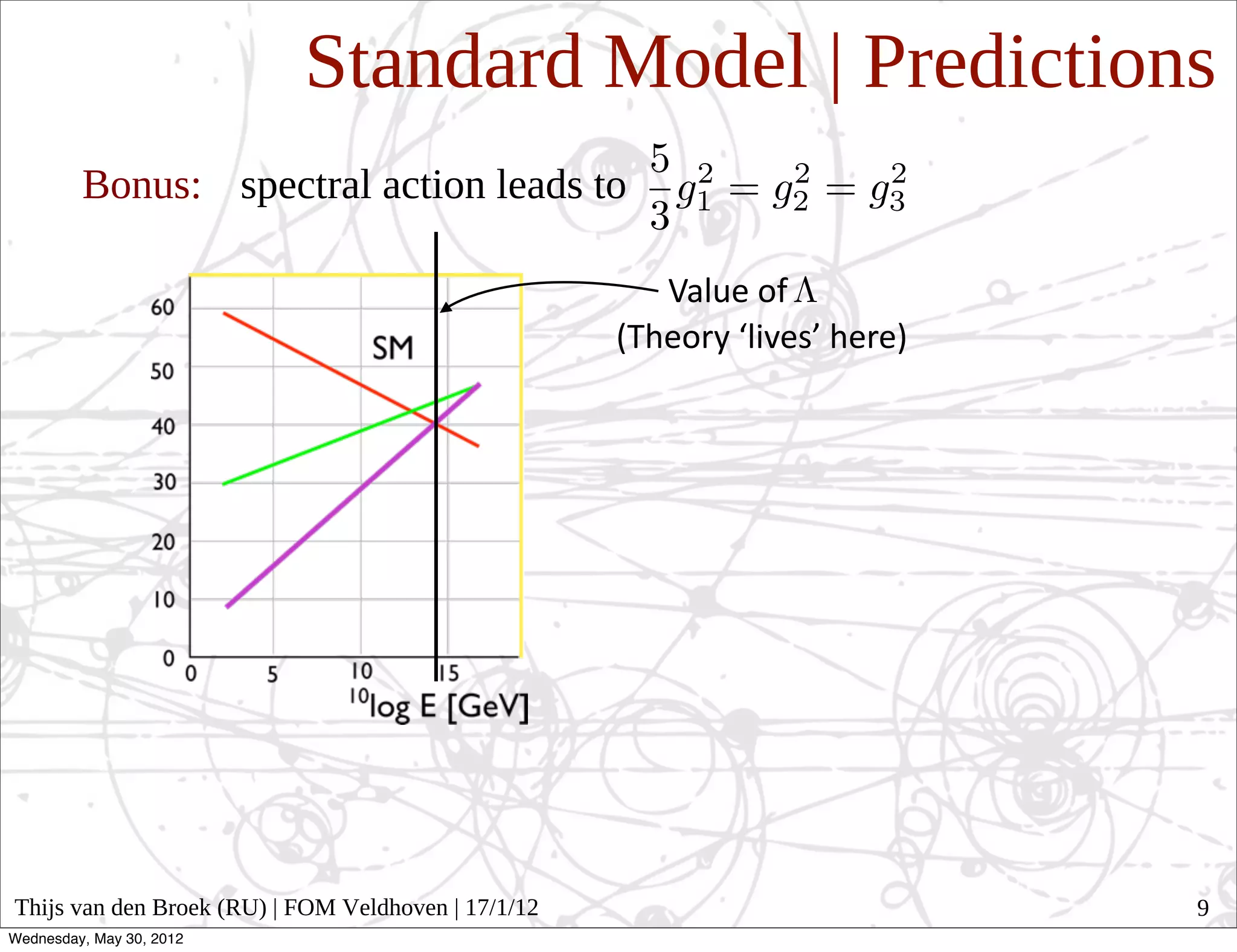
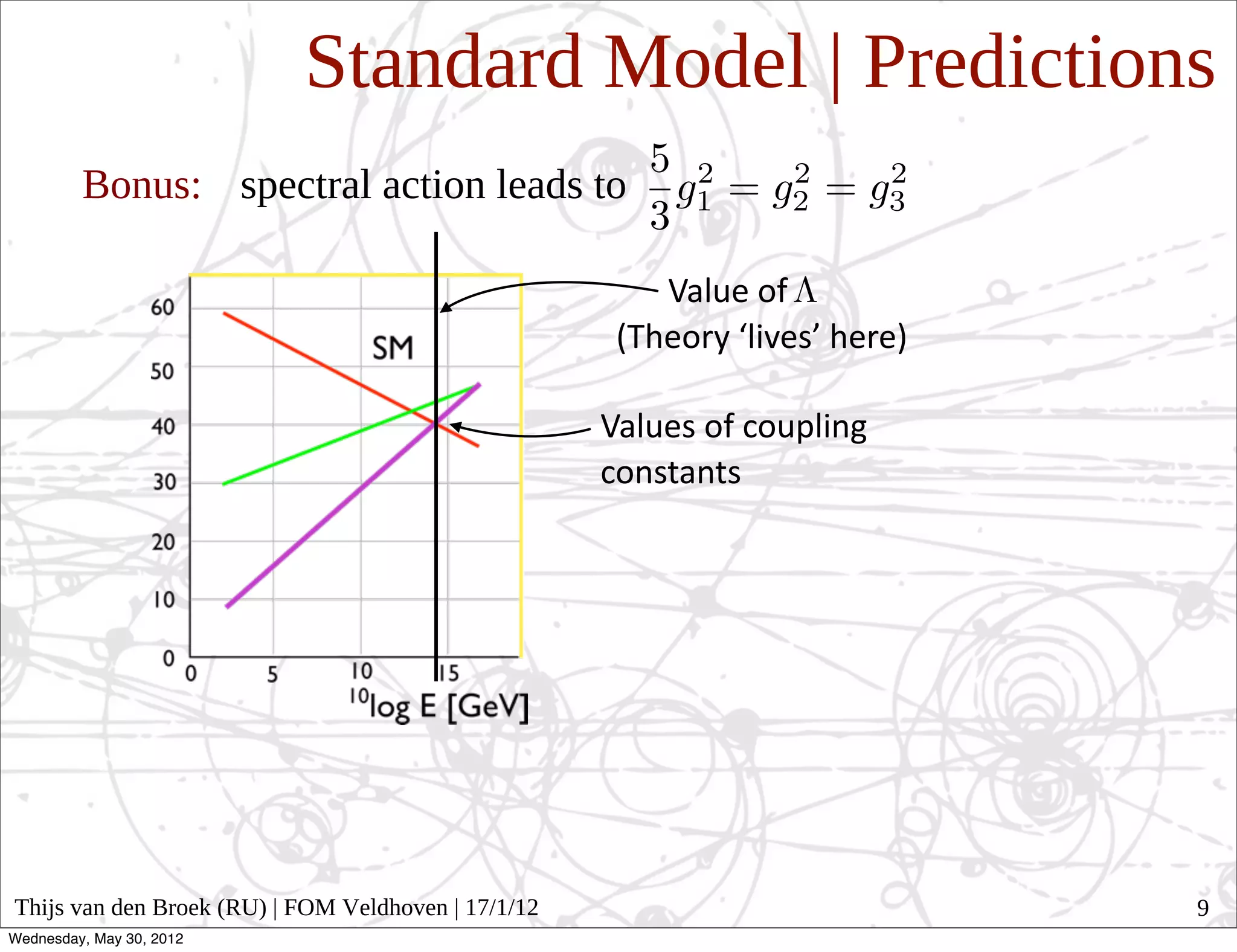
The document discusses noncommutative geometry and its relationship to physics. It begins by explaining how general relativity describes spacetime as curved via metrics. Noncommutative geometry generalizes this idea by replacing the commutative algebra of functions on a space with a noncommutative algebra, treating the coordinates as operators. This allows geometry to be defined even when coordinates do not commute. The document then discusses how noncommutative geometry can provide insights into formulating theories like general relativity and the standard model in terms of geometry. It suggests noncommutative geometry may offer a unified geometric understanding of fundamental physics.

1. Non[com,mut]ative geometry
&
Supersymmetry
yrtemmysrepuS
Is | Thijs van den Broek
From | Radboud University Nijmegen / Nikhef
With | Walter van Suijlekom & Wim Beenakker
Wednesday, May 30, 2012

2. Geometry & physics
Classical physics: flat space, time
Thijs van den Broek (RU) | FOM Veldhoven | 17/1/12
Wednesday, May 30, 2012

3. Geometry & physics
Classical physics: flat space, time
General relativity (Einstein, 1916):
Thijs van den Broek (RU) | FOM Veldhoven | 17/1/12
Wednesday, May 30, 2012

4. Geometry & physics
Classical physics: flat space, time
General relativity (Einstein, 1916):
Curved spacetime
Thijs van den Broek (RU) | FOM Veldhoven | 17/1/12
Wednesday, May 30, 2012

5. Geometry & physics
Classical physics: flat space, time
General relativity (Einstein, 1916):
Curved spacetime
Metric
Thijs van den Broek (RU) | FOM Veldhoven | 17/1/12
Wednesday, May 30, 2012

6. Geometry & physics
Classical physics: flat space, time
General relativity (Einstein, 1916):
Curved spacetime
Metric
Einstein equations:
Thijs van den Broek (RU) | FOM Veldhoven | 17/1/12
Wednesday, May 30, 2012

7. Geometry & physics
Classical physics: flat space, time
General relativity (Einstein, 1916):
Curved spacetime
Metric
Einstein equations:
Or: Einstein - Hilbert action
Thijs van den Broek (RU) | FOM Veldhoven | 17/1/12
Wednesday, May 30, 2012

8. ? Does this set-up allow for
generalisations to
noncommutative spaces
Wednesday, May 30, 2012
3

9. Noncommutative geometry | Basics
Analogy:
QM:
Thijs van den Broek (RU) | FOM Veldhoven | 17/1/12 4
Wednesday, May 30, 2012

10. Noncommutative geometry | Basics
Analogy:
QM: acting on wave functions.
Thijs van den Broek (RU) | FOM Veldhoven | 17/1/12 4
Wednesday, May 30, 2012

11. Noncommutative geometry | Basics
Analogy:
QM: acting on wave functions.
Thijs van den Broek (RU) | FOM Veldhoven | 17/1/12 4
Wednesday, May 30, 2012

12. Noncommutative geometry | Basics
Analogy:
QM: acting on wave functions.
Extend geometry to noncommutative geometry:
Thijs van den Broek (RU) | FOM Veldhoven | 17/1/12 4
Wednesday, May 30, 2012

13. Noncommutative geometry | Basics
Analogy:
QM: acting on wave functions.
Extend geometry to noncommutative geometry:
Thijs van den Broek (RU) | FOM Veldhoven | 17/1/12 4
Wednesday, May 30, 2012

14. Noncommutative geometry | Basics
Analogy:
QM: acting on wave functions.
Extend geometry to noncommutative geometry:
Noncommutative space (...)
Thijs van den Broek (RU) | FOM Veldhoven | 17/1/12 4
Wednesday, May 30, 2012

15. Noncommutative geometry | Basics
Analogy:
QM: acting on wave functions.
Extend geometry to noncommutative geometry:
Noncommutative space (...)
Thijs van den Broek (RU) | FOM Veldhoven | 17/1/12 4
Wednesday, May 30, 2012

16. Noncommutative geometry | Basics
Analogy:
QM: acting on wave functions.
Extend geometry to noncommutative geometry:
Determines metric
Noncommutative space (...)
Thijs van den Broek (RU) | FOM Veldhoven | 17/1/12 4
Wednesday, May 30, 2012

17. Noncommutative geometry | Basics
Analogy:
QM: acting on wave functions.
Extend geometry to noncommutative geometry:
Fermions / spinors
Determines metric
Noncommutative space (...)
Thijs van den Broek (RU) | FOM Veldhoven | 17/1/12 4
Wednesday, May 30, 2012

18. Noncommutative geometry | Basics
Analogy:
QM: acting on wave functions.
Extend geometry to noncommutative geometry:
Fermions / spinors
Determines metric
Noncommutative space (...)
Thijs van den Broek (RU) | FOM Veldhoven | 17/1/12 4
Wednesday, May 30, 2012

19. Noncommutative geometry | Basics
Analogy:
QM: acting on wave functions.
Extend geometry to noncommutative geometry:
Fermions / spinors
Determines metric
Noncommutative space (...)
GRT is a special example.
Thijs van den Broek (RU) | FOM Veldhoven | 17/1/12 4
Wednesday, May 30, 2012

20. NCG | Details
To be a bit more precise, we’re working with in the case
of GRT:
5
Wednesday, May 30, 2012

21. NCG | Details
To be a bit more precise, we’re working with in the case
of GRT:
5
Wednesday, May 30, 2012

22. NCG | Details
To be a bit more precise, we’re working with in the case
of GRT:
5
Wednesday, May 30, 2012

23. NCG | Details
To be a bit more precise, we’re working with in the case
of GRT:
5
Wednesday, May 30, 2012

24. NCG | Details
To be a bit more precise, we’re working with in the case
of GRT:
5
Wednesday, May 30, 2012

25. NCG | Details
To be a bit more precise, we’re working with in the case
of GRT:
5
Wednesday, May 30, 2012

26. NCG | Details
To be a bit more precise, we’re working with in the case
of GRT:
5
Wednesday, May 30, 2012

27. NCG | Details
To be a bit more precise, we’re working with in the case
of GRT:
5
Wednesday, May 30, 2012

28. NCG | Details
To be a bit more precise, we’re working with in the case
of GRT:
5
Wednesday, May 30, 2012

29. NCG | Details
To be a bit more precise, we’re working with in the case
of GRT:
5
Wednesday, May 30, 2012

30. NCG | Action
Wish: An action
Thijs van den Broek (RU) | FOM Veldhoven | 17/1/12 6
Wednesday, May 30, 2012

31. NCG | Action
Wish: An action
Ac#on / Feynman Cross
Lagrangian rules sec#ons
Thijs van den Broek (RU) | FOM Veldhoven | 17/1/12 6
Wednesday, May 30, 2012

32. NCG | Action
Wish: An action
That is fixed by the noncommutative geometry
Ac#on / Feynman Cross
Lagrangian rules sec#ons
Thijs van den Broek (RU) | FOM Veldhoven | 17/1/12 6
Wednesday, May 30, 2012

33. NCG | Action
Wish: An action
That is fixed by the noncommutative geometry
NCG Ac#on / Feynman Cross
Lagrangian rules sec#ons
Thijs van den Broek (RU) | FOM Veldhoven | 17/1/12 6
Wednesday, May 30, 2012

34. NCG | Action
Wish: An action
That is fixed by the noncommutative geometry
NCG Ac#on / Feynman Cross
Lagrangian rules sec#ons
‘Spectral action’:
Thijs van den Broek (RU) | FOM Veldhoven | 17/1/12 6
Wednesday, May 30, 2012

35. NCG | Action
Wish: An action
That is fixed by the noncommutative geometry
NCG Ac#on / Feynman Cross
Lagrangian rules sec#ons
‘Spectral action’:
Analogy:
Thijs van den Broek (RU) | FOM Veldhoven | 17/1/12 6
Wednesday, May 30, 2012

36. NCG | Action
Wish: An action
That is fixed by the noncommutative geometry
NCG Ac#on / Feynman Cross
Lagrangian rules sec#ons
‘Spectral action’:
Analogy:
Thijs van den Broek (RU) | FOM Veldhoven | 17/1/12 6
Wednesday, May 30, 2012

37. NCG | Action
Wish: An action
That is fixed by the noncommutative geometry
NCG Ac#on / Feynman Cross
Lagrangian rules sec#ons
‘Spectral action’:
Analogy:
Thijs van den Broek (RU) | FOM Veldhoven | 17/1/12 6
Wednesday, May 30, 2012

38. NCG | Action
Wish: An action
That is fixed by the noncommutative geometry
NCG Ac#on / Feynman Cross
Lagrangian rules sec#ons
‘Spectral action’:
Analogy:
Thijs van den Broek (RU) | FOM Veldhoven | 17/1/12 6
Wednesday, May 30, 2012

39. NCG | Action
Wish: An action
That is fixed by the noncommutative geometry
NCG Ac#on / Feynman Cross
Lagrangian rules sec#ons
‘Spectral action’:
Analogy:
Thijs van den Broek (RU) | FOM Veldhoven | 17/1/12 6
Wednesday, May 30, 2012

40. NCG | Action
Wish: An action
That is fixed by the noncommutative geometry
NCG Ac#on / Feynman Cross
Lagrangian rules sec#ons
‘Spectral action’:
Analogy:
Thijs van den Broek (RU) | FOM Veldhoven | 17/1/12 6
Wednesday, May 30, 2012

41. NCG | Action
Wish: An action
That is fixed by the noncommutative geometry
NCG Ac#on / Feynman Cross
Lagrangian rules sec#ons
‘Spectral action’:
Analogy:
GRT: gives Einstein - Hilbert action + more ( )
Thijs van den Broek (RU) | FOM Veldhoven | 17/1/12 6
Wednesday, May 30, 2012

42. ? How different are the internal
and external degrees of
freedom of a particle?
Wednesday, May 30, 2012

43. Standard Model | Set up
The geometry:
Thijs van den Broek (RU) | FOM Veldhoven | 17/1/12 8
Wednesday, May 30, 2012

44. Standard Model | Set up
The geometry:
Thijs van den Broek (RU) | FOM Veldhoven | 17/1/12 8
Wednesday, May 30, 2012

45. Standard Model | Set up
The geometry:
Thijs van den Broek (RU) | FOM Veldhoven | 17/1/12 8
Wednesday, May 30, 2012

46. Standard Model | Set up
“Gauge group”
The geometry: (internal degrees of freedom)
Curved spacetime
(external degrees of freedom)
Thijs van den Broek (RU) | FOM Veldhoven | 17/1/12 8
Wednesday, May 30, 2012

47. Standard Model | Set up
“Gauge group”
The geometry: (internal degrees of freedom)
Curved spacetime
(external degrees of freedom)
Choice for F automatically gives fermions (spinors)
‘inner structure’ (i.e. color etc).
Thijs van den Broek (RU) | FOM Veldhoven | 17/1/12 8
Wednesday, May 30, 2012

48. Standard Model | Set up
“Gauge group”
The geometry: (internal degrees of freedom)
Curved spacetime
(external degrees of freedom)
Choice for F automatically gives fermions (spinors)
‘inner structure’ (i.e. color etc).
Can naturally coincide with the SM particle content.
Thijs van den Broek (RU) | FOM Veldhoven | 17/1/12 8
Wednesday, May 30, 2012

49. Standard Model | Set up
“Gauge group”
The geometry: (internal degrees of freedom)
Curved spacetime
(external degrees of freedom)
Choice for F automatically gives fermions (spinors)
‘inner structure’ (i.e. color etc).
Can naturally coincide with the SM particle content.
Spectral action gives:
General Relativity + Standard Model + more ( )
Thijs van den Broek (RU) | FOM Veldhoven | 17/1/12 8
Wednesday, May 30, 2012

50. Standard Model | Set up
“Gauge group”
The geometry: (internal degrees of freedom)
Curved spacetime
(external degrees of freedom)
Choice for F automatically gives fermions (spinors)
‘inner structure’ (i.e. color etc).
Can naturally coincide with the SM particle content.
Spectral action gives:
General Relativity + Standard Model + more ( )
A geometrical understanding of the Standard Model!
Thijs van den Broek (RU) | FOM Veldhoven | 17/1/12 8
Wednesday, May 30, 2012

51. Standard Model | Predictions
Bonus: spectral action leads to
Thijs van den Broek (RU) | FOM Veldhoven | 17/1/12 9
Wednesday, May 30, 2012

52. Standard Model | Predictions
Bonus: spectral action leads to
Thijs van den Broek (RU) | FOM Veldhoven | 17/1/12 9
Wednesday, May 30, 2012

53. Standard Model | Predictions
Bonus: spectral action leads to
Value of
(Theory ‘lives’ here)
Thijs van den Broek (RU) | FOM Veldhoven | 17/1/12 9
Wednesday, May 30, 2012

54. Standard Model | Predictions
Bonus: spectral action leads to
Value of
(Theory ‘lives’ here)
Values of coupling
constants
Thijs van den Broek (RU) | FOM Veldhoven | 17/1/12 9
Wednesday, May 30, 2012

55. Standard Model | Predictions
Bonus: spectral action leads to
Value of
(Theory ‘lives’ here)
Values of coupling
constants
Thijs van den Broek (RU) | FOM Veldhoven | 17/1/12 9
Wednesday, May 30, 2012

56. Standard Model | Predictions
Bonus: spectral action leads to
Value of
(Theory ‘lives’ here)
Values of coupling
constants
Higgs mass predic#on: 158 -­‐ 173 GeV
Thijs van den Broek (RU) | FOM Veldhoven | 17/1/12 9
Wednesday, May 30, 2012

57. Supersymmetry & MSSM
N = 1 supersymmetry: each particle in the theory has a
superpartner, differing in spin by 1/2...
Thijs van den Broek (RU) | FOM Veldhoven | 17/1/12 10
Wednesday, May 30, 2012

58. Supersymmetry & MSSM
N = 1 supersymmetry: each particle in the theory has a
superpartner, differing in spin by 1/2...
... such that action is invariant under supersymmetry
transformations.
Thijs van den Broek (RU) | FOM Veldhoven | 17/1/12 10
Wednesday, May 30, 2012

59. Supersymmetry & MSSM
N = 1 supersymmetry: each particle in the theory has a
superpartner, differing in spin by 1/2...
... such that action is invariant under supersymmetry
transformations.
MSSM: N = 1 supersymmetric version of SM:
Thijs van den Broek (RU) | FOM Veldhoven | 17/1/12 10
Wednesday, May 30, 2012

60. Supersymmetry & MSSM
N = 1 supersymmetry: each particle in the theory has a
superpartner, differing in spin by 1/2...
... such that action is invariant under supersymmetry
transformations.
MSSM: N = 1 supersymmetric version of SM:
Chiral fermions (quarks, leptons)
Gauge bosons (gluons, ...)
Thijs van den Broek (RU) | FOM Veldhoven | 17/1/12 10
Wednesday, May 30, 2012

61. Supersymmetry & MSSM
N = 1 supersymmetry: each particle in the theory has a
superpartner, differing in spin by 1/2...
... such that action is invariant under supersymmetry
transformations.
MSSM: N = 1 supersymmetric version of SM:
Chiral fermions (quarks, leptons) Sfermions (squarks, sleptons)
Gauge bosons (gluons, ...) Gauginos (gluinos, ...)
Thijs van den Broek (RU) | FOM Veldhoven | 17/1/12 10
Wednesday, May 30, 2012

62. Supersymmetry & MSSM
N = 1 supersymmetry: each particle in the theory has a
superpartner, differing in spin by 1/2...
... such that action is invariant under supersymmetry
transformations.
MSSM: N = 1 supersymmetric version of SM:
Chiral fermions (quarks, leptons) Sfermions (squarks, sleptons)
Gauge bosons (gluons, ...) Gauginos (gluinos, ...)
Possible solution for various (theoretical) problems
(e.g. provides dark matter candidate).
Thijs van den Broek (RU) | FOM Veldhoven | 17/1/12 10
Wednesday, May 30, 2012

63. NCG & Supersymmetry
Complication:
Different origins of
particles
Thijs van den Broek (RU) | FOM Veldhoven | 17/1/12 11
Wednesday, May 30, 2012

64. NCG & Supersymmetry
SUSY NCG
Complication: Chiral fermions
Different origins of Sfermions (scalar)
particles Gauge bosons
Gauginos
Thijs van den Broek (RU) | FOM Veldhoven | 17/1/12 11
Wednesday, May 30, 2012

65. NCG & Supersymmetry
SUSY NCG
Complication: Chiral fermions
Different origins of Sfermions (scalar)
particles Gauge bosons
Gauginos
Moreover: different questions:
Thijs van den Broek (RU) | FOM Veldhoven | 17/1/12 11
Wednesday, May 30, 2012

66. NCG & Supersymmetry
SUSY NCG
Complication: Chiral fermions
Different origins of Sfermions (scalar)
particles Gauge bosons
Gauginos
Moreover: different questions:
SUSY: Which actions are supersymmetric?
Thijs van den Broek (RU) | FOM Veldhoven | 17/1/12 11
Wednesday, May 30, 2012

67. NCG & Supersymmetry
SUSY NCG
Complication: Chiral fermions
Different origins of Sfermions (scalar)
particles Gauge bosons
Gauginos
Moreover: different questions:
SUSY: Which actions are supersymmetric?
NCG: For which noncommutative geometries is the
spectral action supersymmetric?
Thijs van den Broek (RU) | FOM Veldhoven | 17/1/12 11
Wednesday, May 30, 2012

68. NCG & Supersymmetry
SUSY NCG
Complication: Chiral fermions
Different origins of Sfermions (scalar)
particles Gauge bosons
Gauginos
Moreover: different questions:
SUSY: Which actions are supersymmetric?
NCG: For which noncommutative geometries is the
spectral action supersymmetric?
Status: ✓ SYM
✓ super-QCD
Thijs van den Broek (RU) | FOM Veldhoven | 17/1/12 11
Wednesday, May 30, 2012

69. NCG & Supersymmetry
SUSY NCG
Complication: Chiral fermions
Different origins of Sfermions (scalar)
particles Gauge bosons
Gauginos
Moreover: different questions:
SUSY: Which actions are supersymmetric?
NCG: For which noncommutative geometries is the
spectral action supersymmetric?
Status: ✓ SYM
✓ super-QCD
General: soon to be finished.
Thijs van den Broek (RU) | FOM Veldhoven | 17/1/12 11
Wednesday, May 30, 2012

70. NCG & Supersymmetry
SUSY NCG
Complication: Chiral fermions
Different origins of Sfermions (scalar)
particles Gauge bosons
Gauginos
Moreover: different questions:
SUSY: Which actions are supersymmetric?
NCG: For which noncommutative geometries is the
spectral action supersymmetric?
Status: ✓ SYM Up next:
✓ super-QCD ? The Higgs mass.
General: soon to be finished.
Thijs van den Broek (RU) | FOM Veldhoven | 17/1/12 11
Wednesday, May 30, 2012

71. I Thank you.
Thijs van den Broek (RU) | FOM Veldhoven | 17/1/12 12
Wednesday, May 30, 2012