The document discusses linear data structures and lists. It introduces the list abstract data type (ADT) and describes common list operations like finding an element or inserting and deleting elements. It also describes different types of lists, including singly linked lists, circularly linked lists, and doubly linked lists. The document then discusses stack and queue ADTs and their applications.




![191ITC301T DATA STRUCTURES AND ALGORITHMS NOTES -I
K.P.REVATHI / ASSISTANT PROFESSOR,AI&DS,EEC |
Linear Data Structures: A data structure is called linear if all of its elements are arranged
in the linear order. In linear data structures, the elements are stored in non-hierarchical way where
each element has the successors and predecessors except the first and last element.
Types of Linear Data Structures are given below:
Arrays: An array is a collection of similar type of data items and each data item is called
an element of the array. The data type of the element may be any valid data type like char, int, float
or double.
The elements of array share the same variable name but each one carries a different index
number known as subscript. The array can be one dimensional, two dimensional or
multidimensional.
The individual elements of the array age are:
age[0], age[1], age[2], age[3],......... age[98], age[99].
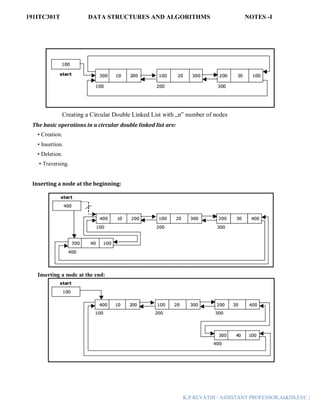
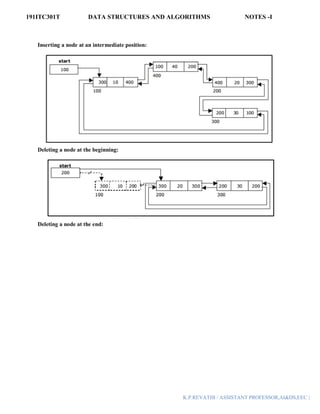
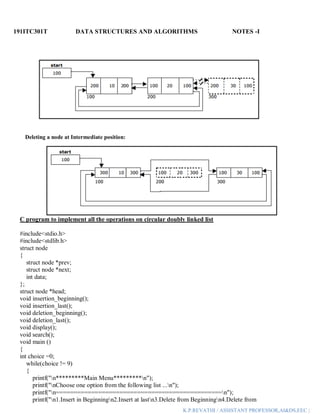
Linked List: Linked list is a linear data structure which is used to maintain a list in the
memory. It can be seen as the collection of nodes stored at non-contiguous memory locations. Each
node of the list contains a pointer to its adjacent node.
Stack: Stack is a linear list in which insertion and deletions are allowed only at one end,
called top.
A stack is an abstract data type (ADT), can be implemented in most of the programming
languages. It is named as stack because it behaves like a real-world stack, for example: - piles of](https://image.slidesharecdn.com/uniti-datastructures-220703042928-c632d447/85/UNIT-I-Data-Structures-pdf-5-320.jpg)






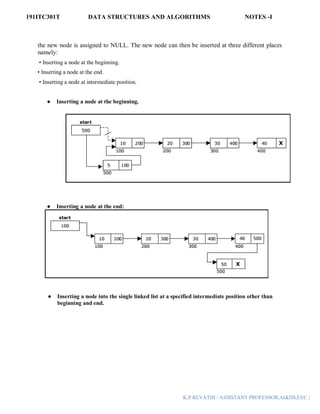














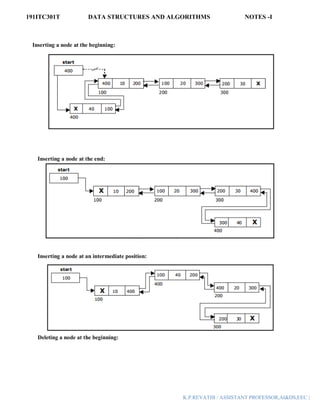
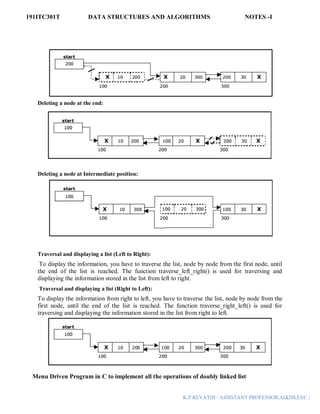














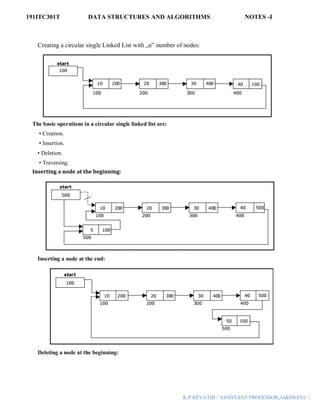












![191ITC301T DATA STRUCTURES AND ALGORITHMS NOTES -I
K.P.REVATHI / ASSISTANT PROFESSOR,AI&DS,EEC |
is full or not. If the stack is full it generates an error message "stack overflow".
Pop:
Pop operation is used to delete elements from the stack. At the time of deletion first check the stack is
empty or not. If the stack is empty it generates an error message "stack underflow".
Representation of a Stack using Arrays:
Let us consider a stack with 6 elements capacity. This is called as the size of the stack. The number of
elements to be added should not exceed the maximum size of the stack. If we attempt to add new element
beyond the maximum size, we will encounter a stack overflow condition. Similarly, you cannot remove
elements beyond the base of the stack. If such is the case, we will reach a stack underflow condition.
When a element is added to a stack, the operation is performed by push().
When an element is taken off from the stack, the operation is performed by pop().
Source code for stack operations, using array:
STACK: Stack is a linear data structure which works under the principle of last in first out. Basic
operations: push, pop, display.
1. PUSH: if (top==MAX), display Stack overflow else reading the data and making stack [top]
=data and incrementing the top value by doing top++.
2. POP: if (top==0), display Stack underflow else printing the element at the top of the stack and
decrementing the top value by doing the top.
3. DISPLAY: IF (TOP==0), display Stack is empty else printing the elements in the stack from stack [0]
to stack [top].
Example:
#include <stdio.h>](https://image.slidesharecdn.com/uniti-datastructures-220703042928-c632d447/85/UNIT-I-Data-Structures-pdf-59-320.jpg)
![191ITC301T DATA STRUCTURES AND ALGORITHMS NOTES -I
K.P.REVATHI / ASSISTANT PROFESSOR,AI&DS,EEC |
int stack[100],i,j,choice=0,n,top=-1;
void push();
void pop();
void show();
void main ()
{
printf("Enter the number of elements in the stack ");
scanf("%d",&n);
printf("*********Stack operations using array*********");
printf("n----------------------------------------------n");
while(choice != 4)
{
printf("Chose one from the below options...n");
printf("n1.Pushn2.Popn3.Shown4.Exit");
printf("n Enter your choice n");
scanf("%d",&choice);
switch(choice)
{
case 1:
{
push();
break;
}
case 2:
{
pop();
break;
}
case 3:
{
show();
break;
}
case 4:
{
printf("Exiting....");
break;
}
default:
{
printf("Please Enter valid choice ");
}
};
}
}](https://image.slidesharecdn.com/uniti-datastructures-220703042928-c632d447/85/UNIT-I-Data-Structures-pdf-60-320.jpg)
![191ITC301T DATA STRUCTURES AND ALGORITHMS NOTES -I
K.P.REVATHI / ASSISTANT PROFESSOR,AI&DS,EEC |
void push ()
{
int val;
if (top == n )
printf("n Overflow");
else
{
printf("Enter the value?");
scanf("%d",&val);
top = top +1;
stack[top] = val;
}
}
void pop ()
{
if(top == -1)
printf("Underflow");
else
top = top -1;
}
void show()
{
for (i=top;i>=0;i--)
{
printf("%dn",stack[i]);
}
if(top == -1)
{
printf("Stack is empty");
}
}
Linked List Implementation of Stacks
The first implementation of a stack uses a singly linked list. We perform a push by inserting
at the front of the list. We perform a pop by deleting the element at the front of the list. A top operation
merely examines the element at the front of the list, returning its value. Sometimes the pop and top
operations are combined into one.
Creating an empty stack is also simple. We merely create a header node; make_null sets the
next pointer to NULL.
The push is implemented as an insertion into the front of a linked list, where the front of the](https://image.slidesharecdn.com/uniti-datastructures-220703042928-c632d447/85/UNIT-I-Data-Structures-pdf-61-320.jpg)




![191ITC301T DATA STRUCTURES AND ALGORITHMS NOTES -I
K.P.REVATHI / ASSISTANT PROFESSOR,AI&DS,EEC |
free( first_cell );
} }
Stack Applications
Stack is used for the following applications.
1. Reversing of the string
2. Tower’s of Hanoi’s problem
3. Balancing Symbols
4. Conversion of Infix to postfix expression
5. Conversion of Infix to prefix expression
6. Evaluation of Postfix expression
7. Used in Function calls
Balancing Symbols
Compilers check your programs for syntax errors, but frequently a lack of one symbol
(such as a missing brace or comment starter) will cause the compiler to
spill out a hundred lines of diagnostics without identifying the real error.
A useful tool in this situation is a program that checks whether everything is balanced.
Thus, every right brace, bracket, and parenthesis must correspond to
their left counterparts.
The sequence [()] is legal, but [(]) is wrong. That it is easy to check these things. For simplicity,
we will just check for balancing of parentheses, brackets, and braces and ignore any other character
that appears.](https://image.slidesharecdn.com/uniti-datastructures-220703042928-c632d447/85/UNIT-I-Data-Structures-pdf-66-320.jpg)









![191ITC301T DATA STRUCTURES AND ALGORITHMS NOTES -I
K.P.REVATHI / ASSISTANT PROFESSOR,AI&DS,EEC |
Queue Model
The basic operations on a queue are
1. enqueue, which inserts an element at the end of the list (called the rear)
2. dequeue, which deletes (and returns) the element at the start of the list (known as
the front).
Abstract model of a queue
Array Implementation of Queues
● Like stacks, both the linked list and array implementations give fast O(1) running times for
every operation. The linked list implementation is straightforward and left as an exercise. We
will now discuss an array implementation of queues.
● For each queue data structure, we keep an array, QUEUE[], and the positions q_front and
q_rear, which represent the ends of the queue. We also keep track of the number of elements
that are actually in the queue, q_size.
The following figure shows a queue in some intermediate state.
● By the way, the cells that are blanks have undefined values in them. In particular, the first
two cells have elements that used to be in the queue.
● To enqueue an element x, we increment q_size and q_rear, then set QUEUE[q_rear] = x.](https://image.slidesharecdn.com/uniti-datastructures-220703042928-c632d447/85/UNIT-I-Data-Structures-pdf-76-320.jpg)
![191ITC301T DATA STRUCTURES AND ALGORITHMS NOTES -I
K.P.REVATHI / ASSISTANT PROFESSOR,AI&DS,EEC |
● To dequeue an element, we set the return value to QUEUE[q_front], decrement
q_size, and then increment q_front.. After 10 enqueues, the queue appears to be full, since
q_front is now 10, and the next enqueue would be in a nonexistent position.
● However, there might only be a few elements in the queue, because several elements may
have already been dequeued.
● The simple solution is that whenever q_front or q_rear gets to the end of the array, it is
wrapped around to the beginning. This is known as a circular array implementation.
If incrementing either q_rear or q_front causes it to go past the array, the value is reset to the first
position in the array.
There are two warnings about the circular array implementation of queues.
● First, it is important to check the queue for emptiness, because a dequeue when the queue is
empty will return an undefined value.
● Secondly, some programmers use different ways of representing the front and rear of a queue.
For instance, some do not use an entry to keep track of the size, because they rely on the base
case that when the queue is empty, q_rear = q_front - 1.
If the size is not part of the structure, then if the array size is A_SIZE, the queue is full when there
are A_SIZE -1 elements.
In applications where you are sure that the number of enqueues is not larger than the size
of the queue, the wraparound is not necessary.
The routine queue_create and queue_dispose routines also need to be provided. We also
provide routines to test whether a queue is empty and to make an empty queue.
Notice that q_rear is preinitialized to 1 before q_front. The final operation we will write is
the enqueue routine.
Type declarations for queue--array implementation
struct QueueRecord
{
int Capacity;](https://image.slidesharecdn.com/uniti-datastructures-220703042928-c632d447/85/UNIT-I-Data-Structures-pdf-77-320.jpg)


![191ITC301T DATA STRUCTURES AND ALGORITHMS NOTES -I
K.P.REVATHI / ASSISTANT PROFESSOR,AI&DS,EEC |
value = 0; return
value; }
Void enqueue( Elementtype x, Queue Q )
{
if( isfull( Q ) )
error("Full queue");
else
{
Q->Size++;
Q->Rear = succ( Q->Rear, Q ); Q-
>Array[ Q->Rear ] = x;
} }
Applications of Queues
The applications are,
1. When jobs are submitted to a printer, they are arranged in order of arrival. Then jobs sent to
a line printer are placed on a queue.
2. Lines at ticket counters are queues, because service is first-come first-served.
3. Another example concerns computer networks. There are many network setups of personal
computers in which the disk is attached to one machine, known as the file server.
4. Users on other machines are given access to files on a first-come first-served basis, so the
data structure is a queue.](https://image.slidesharecdn.com/uniti-datastructures-220703042928-c632d447/85/UNIT-I-Data-Structures-pdf-80-320.jpg)

![191GES205T PROGRAMMING AND DATA STRUCTURES USING C UNIT-II NOTES
82
In Circular Queue, the insertion of a new element is performed at the very first locations of the
queue if the last location of the queue is full, in which the first element comes after the last
element.
Advantages:
It overcomes the problem of unutilized space in linear queue, when it is implemented as arrays.
To perform the insertion of the element to the queue, the position of the element is calculated as
rear= (rear+1) % queue_size and set Q[rear]=value.
Similarly the element deleted from the queue using front = (front + 1) % queue_size.
Enqueue:
This routine insert the new element at rear position of the circular queue.](https://image.slidesharecdn.com/uniti-datastructures-220703042928-c632d447/85/UNIT-I-Data-Structures-pdf-82-320.jpg)
![191GES205T PROGRAMMING AND DATA STRUCTURES USING C UNIT-II NOTES
83
Dequeue:
This routine deletes the element from the front of the circular queue. void
CQ_dequeue( )
{
If(front==-1 && rear==-1)
Print(“Queue is empty”); Else
{
Temp=CQueue[front];
If(front==rear) Front=rear=-
1;
Else
Front=(front+1)% maxsize;
} }](https://image.slidesharecdn.com/uniti-datastructures-220703042928-c632d447/85/UNIT-I-Data-Structures-pdf-83-320.jpg)


![191GES205T PROGRAMMING AND DATA STRUCTURES USING C UNIT-II NOTES
86
o Removing the minimum element from the priority queue
As we know that in a max heap, the maximum element is the root node. When we remove the root node, it creates
an empty slot. The last inserted element will be added in this empty slot. Then, this element is compared with the
child nodes, i.e., left-child and right child, and swap with the smaller of the two. It keeps moving down the tree
until the heap property is restored.
Applications of Priority queue
The following are the applications of the priority queue:
o It is used in the Dijkstra's shortest path algorithm.
o It is used in prim's algorithm
o It is used in data compression techniques like Huffman code.
o It is used in heap sort.
o It is also used in operating system like priority scheduling, load balancing and interrupt handling.
Program to create the priority queue using the binary max heap.
#include <stdio.h>
#include <stdio.h>
int heap[40];
int size=-1;
// retrieving the parent node of the child node
int parent(int i)
{
return (i - 1) / 2;
}
// retrieving the left child of the parent node.
int left_child(int i)
{
return i+1;
}
// retrieving the right child of the parent](https://image.slidesharecdn.com/uniti-datastructures-220703042928-c632d447/85/UNIT-I-Data-Structures-pdf-86-320.jpg)
![191GES205T PROGRAMMING AND DATA STRUCTURES USING C UNIT-II NOTES
87
int right_child(int i)
{
return i+2;
}
// Returning the element having the highest priority
int get_Max()
{
return heap[0];
}
//Returning the element having the minimum priority
int get_Min()
{
return heap[size];
}
// function to move the node up the tree in order to restore the heap property.
void moveUp(int i)
{
while (i > 0)
{
// swapping parent node with a child node
if(heap[parent(i)] < heap[i]) {
int temp;
temp=heap[parent(i)];
heap[parent(i)]=heap[i];
heap[i]=temp;
}
// updating the value of i to i/2
i=i/2;
}
}
//function to move the node down the tree in order to restore the heap property.
void moveDown(int k)
{
int index = k;
// getting the location of the Left Child
int left = left_child(k);
if (left <= size && heap[left] > heap[index]) {
index = left;
}](https://image.slidesharecdn.com/uniti-datastructures-220703042928-c632d447/85/UNIT-I-Data-Structures-pdf-87-320.jpg)
![191GES205T PROGRAMMING AND DATA STRUCTURES USING C UNIT-II NOTES
88
// getting the location of the Right Child
int right = right_child(k);
if (right <= size && heap[right] > heap[index]) {
index = right;
}
// If k is not equal to index
if (k != index) {
int temp;
temp=heap[index];
heap[index]=heap[k];
heap[k]=temp;
moveDown(index);
}
}
// Removing the element of maximum priority
void removeMax()
{
int r= heap[0];
heap[0]=heap[size];
size=size-1;
moveDown(0);
}
//inserting the element in a priority queue
void insert(int p)
{
size = size + 1;
heap[size] = p;
// move Up to maintain heap property
moveUp(size);
}
//Removing the element from the priority queue at a given index i.
void delete(int i)
{
heap[i] = heap[0] + 1;
// move the node stored at ith location is shifted to the root node
moveUp(i);
// Removing the node having maximum priority
removeMax();
}](https://image.slidesharecdn.com/uniti-datastructures-220703042928-c632d447/85/UNIT-I-Data-Structures-pdf-88-320.jpg)
![191GES205T PROGRAMMING AND DATA STRUCTURES USING C UNIT-II NOTES
89
int main()
{
// Inserting the elements in a priority queue
insert(20);
insert(19);
insert(21);
insert(18);
insert(12);
insert(17);
insert(15);
insert(16);
insert(14);
int i=0;
printf("Elements in a priority queue are : ");
for(int i=0;i<=size;i++)
{
printf("%d ",heap[i]);
}
delete(2); // deleting the element whose index is 2.
printf("nElements in a priority queue after deleting the element are : ");
for(int i=0;i<=size;i++)
{
printf("%d ",heap[i]);
}
int max=get_Max();
printf("nThe element which is having the highest priority is %d: ",max);
int min=get_Min();
printf("nThe element which is having the minimum priority is : %d",min);
return 0;
}](https://image.slidesharecdn.com/uniti-datastructures-220703042928-c632d447/85/UNIT-I-Data-Structures-pdf-89-320.jpg)