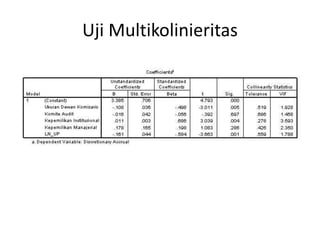
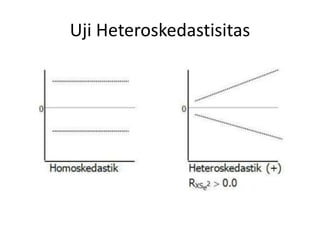
Dokumen ini membahas metode uji hipotesis untuk regresi linier berganda, termasuk uji asumsi klasik seperti normalitas, multikolinieritas, heteroskedastisitas, dan autokorelasi. Uji ini penting untuk memastikan kesesuaian model regresi dan keandalan prediksi yang dihasilkan. Berbagai uji statistik seperti Kolmogorov-Smirnov, VIF, dan Durbin-Watson digunakan untuk menganalisis dan memverifikasi asumsi-asumsi tersebut.