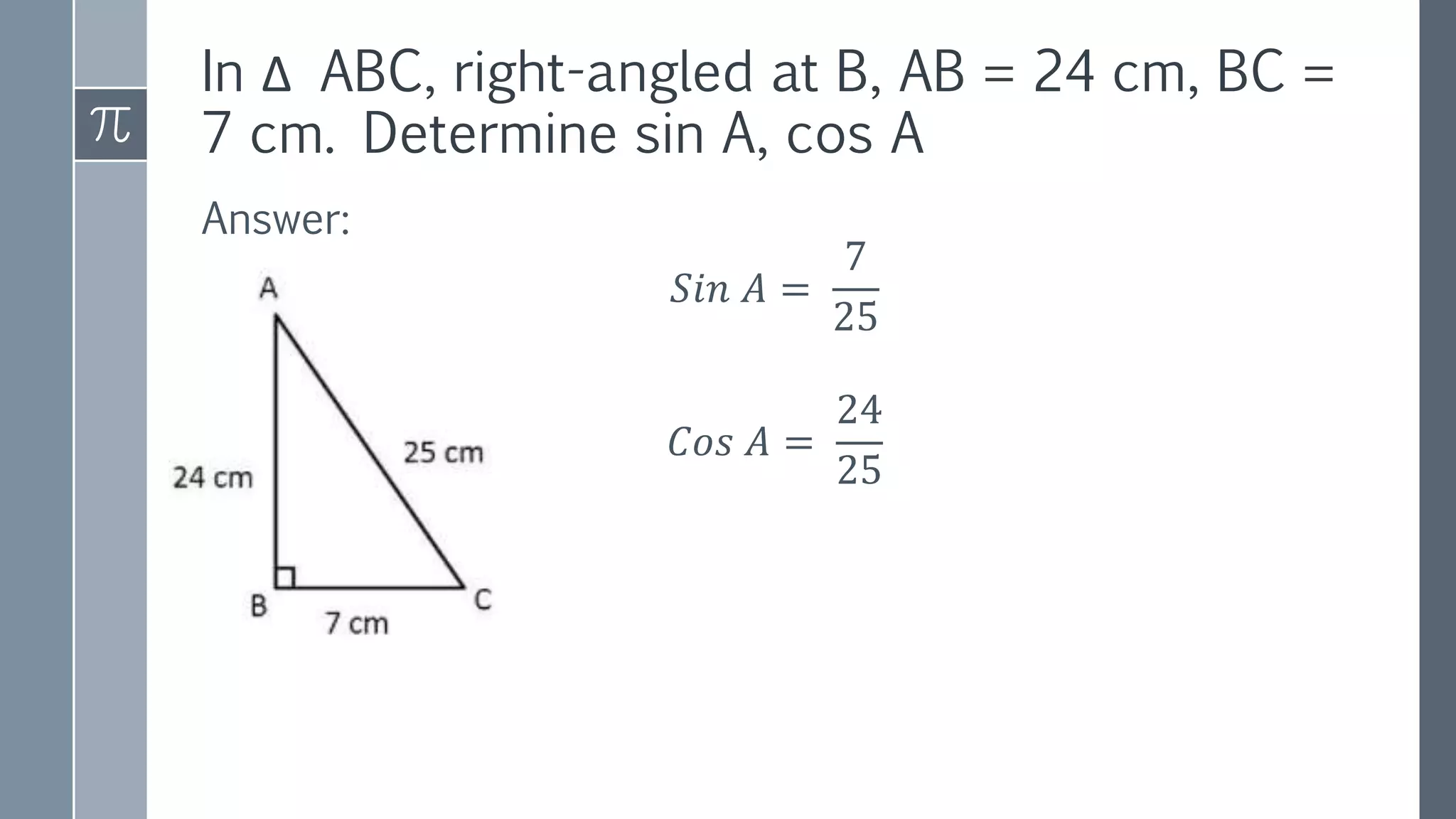
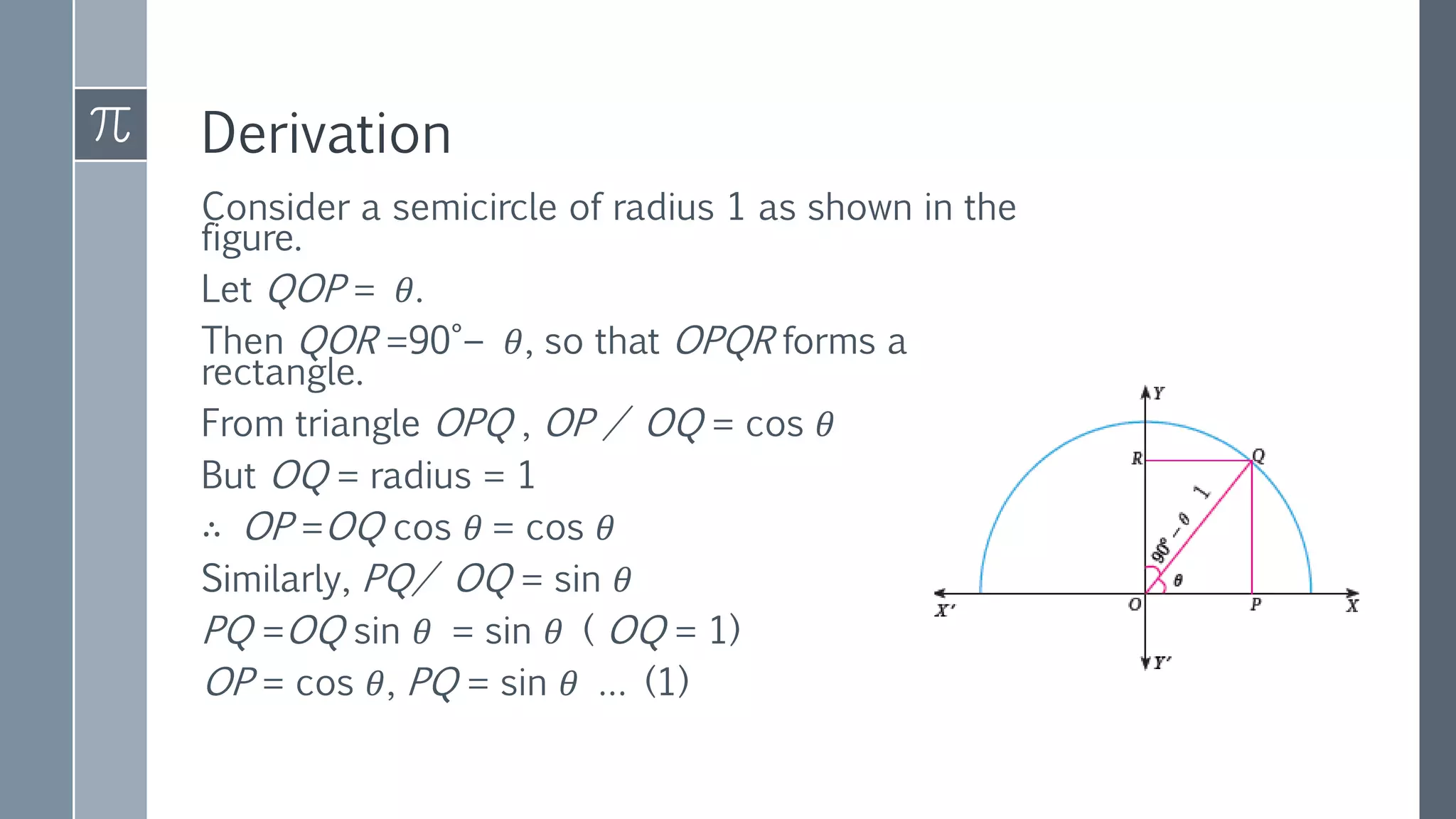
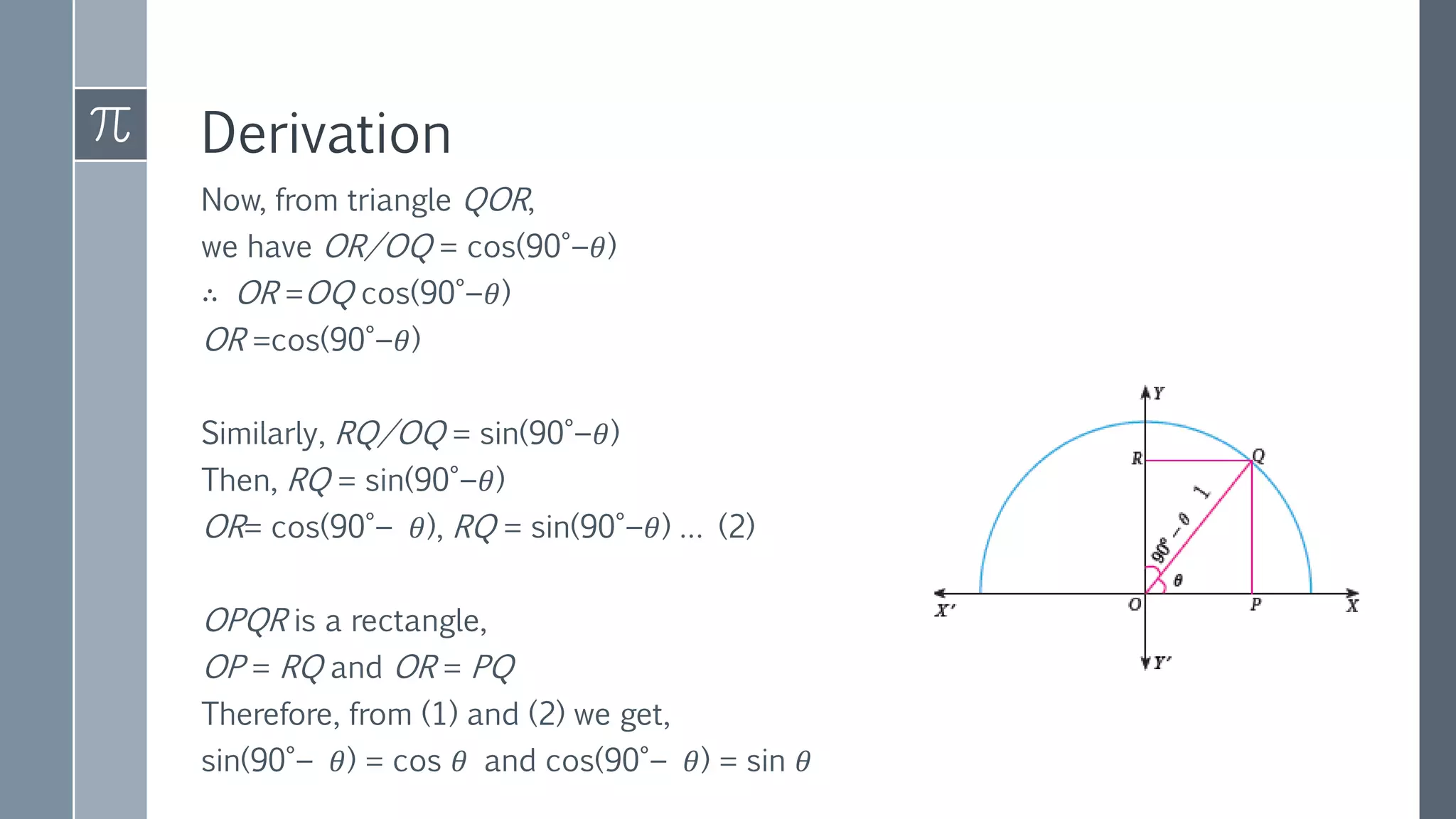
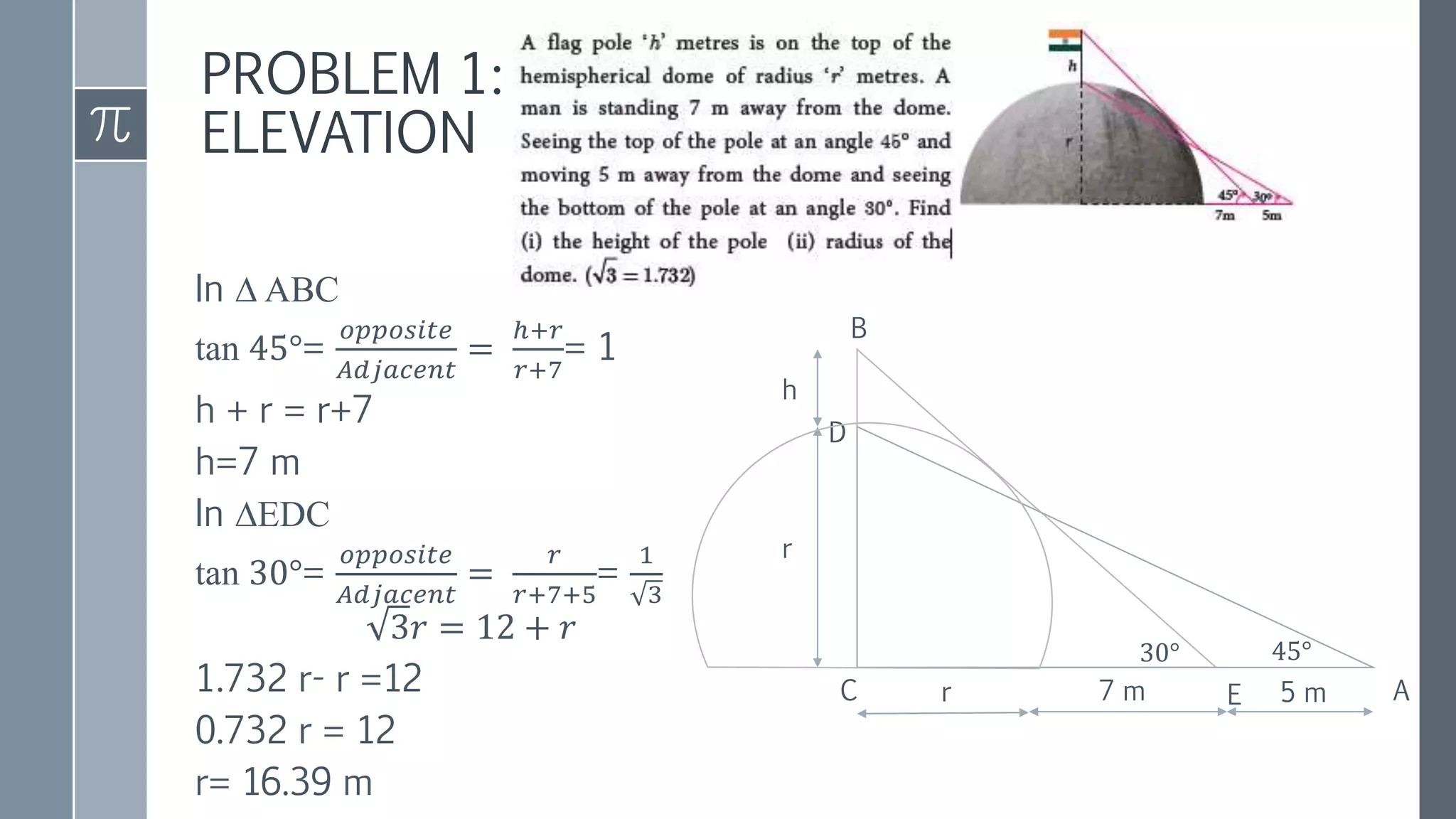
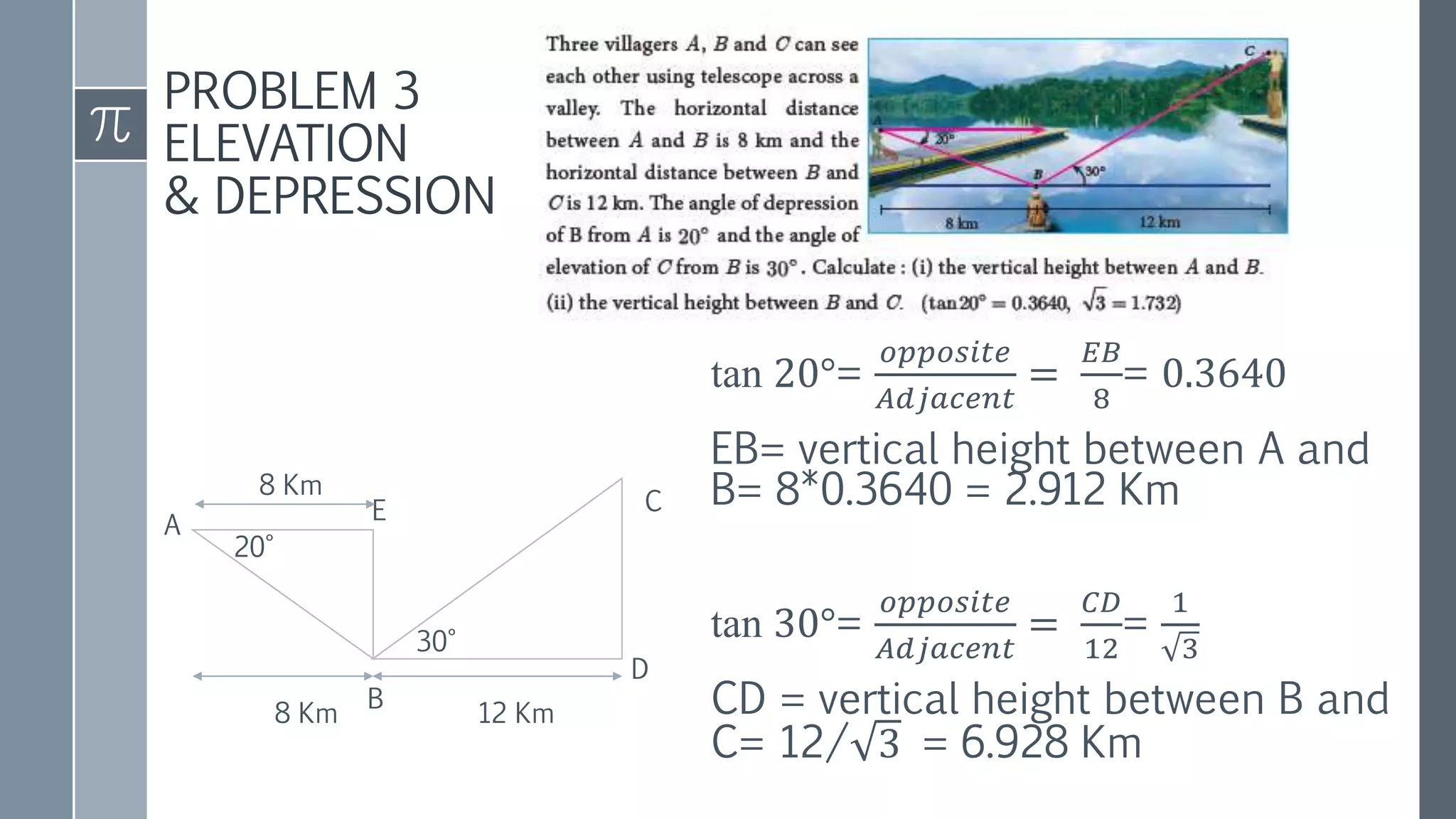
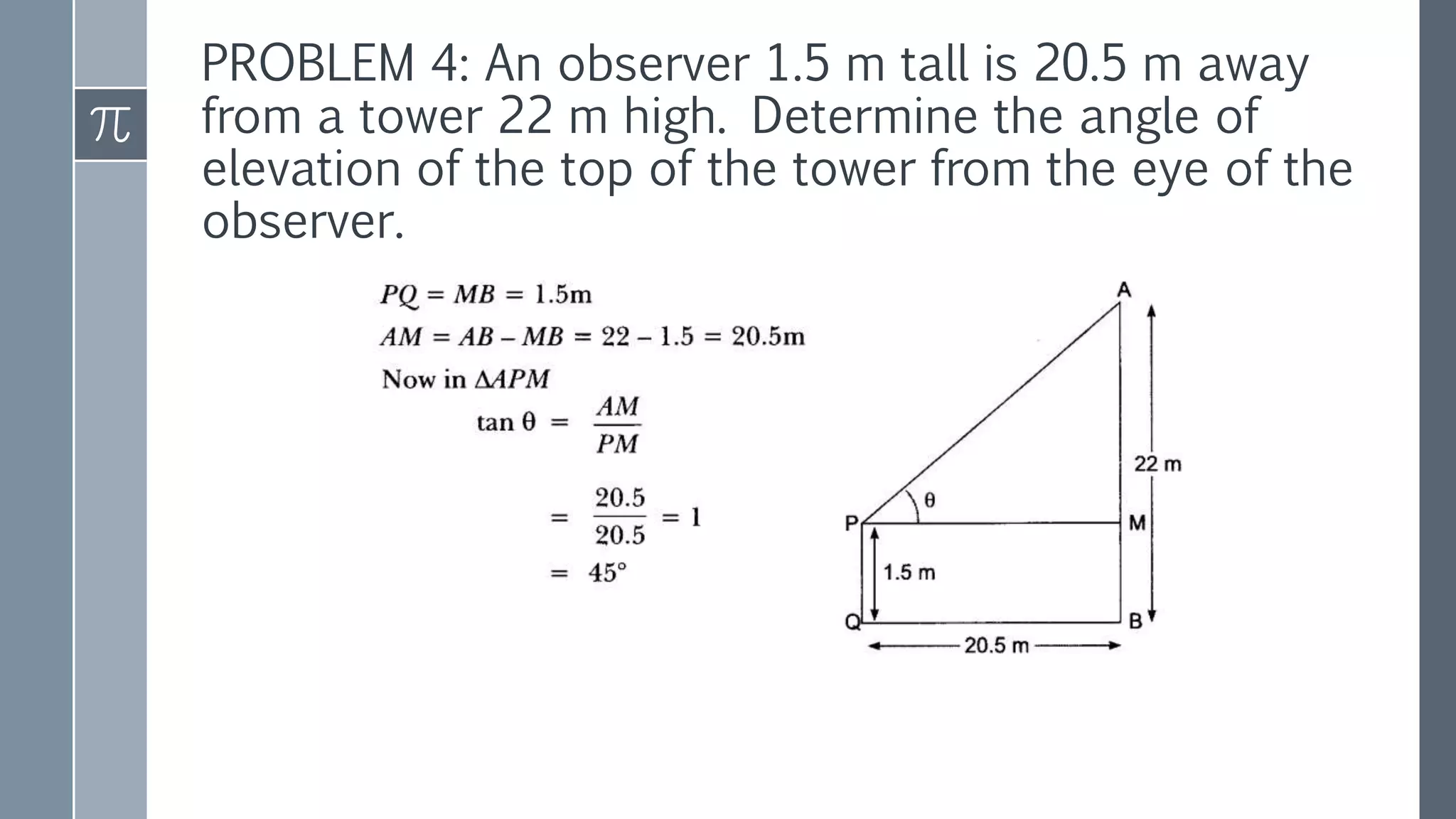
This document discusses trigonometry and its applications. It defines trigonometry as the study of relationships between sides and angles of triangles. It introduces trigonometric ratios like sine, cosine, and tangent and defines them in terms of right triangles. It discusses trigonometric ratios of complementary angles and specific angles like 30, 45, and 60 degrees. It also covers trigonometric identities like the Pythagorean identity and cofunction identities. Finally, it discusses how trigonometry can be used to calculate heights and distances without direct measurement using concepts like line of sight, angle of elevation, and angle of depression.

1. Trigonometry
Unit 6

2. Content
› Trigonometry meaning
› Trigonometric ratios
› Trigonometric ratios of complementary angle
› Trigonometric ratios of Some Specific Angles

3. Trigonometry
› The word ‘trigonometry’ is derived from the Greek words
‘tri’ (meaning three), ‘gon’ (meaning sides) and ‘metron’
(meaning measure). In fact, trigonometry is the study of
relationships between the sides and angles of a triangle.
› Hipparchus is considered as “The Father of
Trigonometry”.

4. Trigonometric ratio
Now we will study some ratios of the sides of a right triangle with
respect to its acute angles, called trigonometric ratios of the angle.
𝑠𝑖𝑛𝑒 𝑜𝑓 ∠ 𝐴 =
𝑠𝑖𝑑𝑒 𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒 𝑡𝑜 ∠𝐴
𝐻𝑦𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑒
=
𝐵𝐶
𝐴𝐶
𝑐𝑜𝑠𝑖𝑛𝑒 𝑜𝑓 ∠ 𝐴 =
𝑠𝑖𝑑𝑒 𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡 𝑡𝑜 ∠𝐴
𝐻𝑦𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑒
=
𝐴𝐵
𝐴𝐶
𝑇𝑎𝑛𝑔𝑒𝑛𝑡 𝑜𝑓 ∠ 𝐴 =
𝑠𝑖𝑑𝑒 𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒 𝑡𝑜 ∠𝐴
𝑠𝑖𝑑𝑒 𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡 𝑡𝑜 ∠ 𝐴
=
𝐵𝐶
𝐴𝐵

5. Trigonometric ratio
𝑇𝑎𝑛𝑔𝑒𝑛𝑡 𝑜𝑓 ∠ 𝐴 =
𝑠𝑖𝑛𝑒 ∠𝐴
𝑐𝑜𝑠𝑖𝑛𝑒 ∠𝐴
=
𝐵𝐶
𝐴𝐶
𝑐𝑜𝑡𝑎𝑛𝑔𝑒𝑛𝑡 𝑜𝑓 ∠ 𝐴 =
𝑐𝑜𝑠𝑖𝑛𝑒 ∠𝐴
𝑠𝑖𝑛𝑒 ∠𝐴
=
𝐴𝐶
𝐵𝐶
Also we see that, 𝑐𝑜𝑡𝑎𝑛𝑔𝑒𝑛𝑡 𝑜𝑓 ∠ 𝐴 =
1
𝑇𝑎𝑛𝑔𝑒𝑛𝑡 ∠𝐴
𝑐𝑜𝑠𝑒𝑐𝑎𝑛𝑡 𝑜𝑓 ∠ 𝐴 =
1
𝑠𝑖𝑛𝑒 ∠𝐴
𝑠𝑒𝑐𝑎𝑛𝑡 𝑜𝑓 ∠ 𝐴 =
1
𝑐𝑜𝑠𝑖𝑛𝑒 ∠𝐴

6. Pneumonic to remember ratios
SOH
SINE is OPPOSITE by
Hypotenuse
CAH
COS is ADJACENT by
Hypotenuse
TOA
TANGENT is OPPOSITE by
Adjacent
For Cosec and sec
Remember two “CO” will not
come together.
𝑐𝑜𝑠𝑒𝑐𝑎𝑛𝑡 𝑜𝑓 ∠ 𝐴 =
1
𝑠𝑖𝑛𝑒 ∠𝐴
𝑠𝑒𝑐𝑎𝑛𝑡 𝑜𝑓 ∠ 𝐴 =
1
𝑐𝑜𝑠𝑖𝑛𝑒 ∠𝐴
Remark : Since the hypotenuse is the longest side in a right triangle, the value
of sin A or cos A is always less than 1 (or, in particular, equal to 1).

7. 𝐻𝑦𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑒2
= 𝐴𝑑𝑗𝑎𝑐𝑒𝑛𝑡2
+ (𝑂𝑝𝑝𝑜𝑠𝑖𝑡𝑒2
)
Recall Pythagoras Theorem,

8. PROBLEM 1
𝑠𝑖𝑛𝑒 𝑜𝑓 ∠ 𝐴 =
𝑠𝑖𝑑𝑒 𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒 𝑡𝑜 ∠𝐴
𝐻𝑦𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑒
=
3
4
Let,
BC= 3X
AC= 4X
Using Pythagoras theorem,
𝐻𝑦𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑒2
= 𝐴𝑑𝑗𝑎𝑐𝑒𝑛𝑡2
+ (𝑂𝑝𝑝𝑜𝑠𝑖𝑡𝑒2
)
(4X2)= (adjacent2) + (3X2)
16X2 = (adjacent2) + 9X2
16X2 – 9X2 = (adjacent2)
7X2 = (adjacent2)
Adjacent = 7𝑋
If sin A = 3 /4 calculate
cos A and tan A.

9. PROBLEM 1
Now we find cos A and Tan A
𝑐𝑜𝑠𝑖𝑛𝑒 𝑜𝑓 ∠ 𝐴 =
𝑠𝑖𝑑𝑒 𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡 𝑡𝑜 ∠𝐴
𝐻𝑦𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑒
=
𝐴𝐵
𝐴𝐶
=
7𝑋
4𝑋
=
7
4
𝑇𝑎𝑛𝑔𝑒𝑛𝑡 𝑜𝑓 ∠ 𝐴 =
𝑠𝑖𝑑𝑒 𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒 𝑡𝑜 ∠𝐴
𝑠𝑖𝑑𝑒 𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡 𝑡𝑜 ∠ 𝐴
=
𝐵𝐶
𝐴𝐵
=
3𝑋
7𝑋
=
3
7
If sin A = 3 /4 calculate
cos A and tan A.

10. In Δ ABC, right-angled at B, AB = 24 cm, BC =
7 cm. Determine sin A, cos A
Answer:
𝑆𝑖𝑛 𝐴 =
7
25
𝐶𝑜𝑠 𝐴 =
24
25

11. Trigonometric ratios of complementary angle
› The sine of any acute angle is equal to the cosine of its
complement and vice versa.
› The cotangent of any acute angle is equal to the tangent
of its complement and vice versa.
› The cosecant of any acute angle is equal to the secant of
its complement and vice versa.
If the sum of two angles is one right angle or 90°, then
one angle is said to be complementary of the other.

12. Derivation
Consider a semicircle of radius 1 as shown in the
figure.
Let QOP = 𝜃.
Then QOR =90°− 𝜃, so that OPQR forms a
rectangle.
From triangle OPQ , OP / OQ = cos 𝜃
But OQ = radius = 1
∴ OP =OQ cos 𝜃 = cos 𝜃
Similarly, PQ/ OQ = sin 𝜃
PQ =OQ sin 𝜃 = sin 𝜃 ( OQ = 1)
OP = cos 𝜃, PQ = sin 𝜃 … (1)

13. Derivation
Now, from triangle QOR,
we have OR/OQ = cos(90°−𝜃)
∴ OR =OQ cos(90°−𝜃)
OR =cos(90°−𝜃)
Similarly, RQ/OQ = sin(90°−𝜃)
Then, RQ = sin(90°−𝜃)
OR= cos(90°− 𝜃), RQ = sin(90°−𝜃) … (2)
OPQR is a rectangle,
OP = RQ and OR = PQ
Therefore, from (1) and (2) we get,
sin(90°− 𝜃) = cos 𝜃 and cos(90°− 𝜃) = sin 𝜃

14. Trigonometric Ratios of Some Specific Angles
Trigonometric Ratios of 30° and 60°
Let us now calculate the trigonometric ratios of 30°
and 60°. Consider an equilateral triangle ABC. Since
each angle in an equilateral triangle is 60°, therefore,
∠ A = ∠ B = ∠ C = 60°.
Draw the perpendicular AD from A to the side BC.
Now Δ ABD ≅ Δ ACD
Therefore, BD = DC
and ∠ BAD = ∠ CAD (CPCT)
Now observe that:
Δ ABD is a right triangle, right-angled at D with
∠ BAD = 30° and ∠ ABD = 60°
3
6

15. Trigonometric Ratios of Some Specific Angles
Trigonometric Ratios of 30° and 60°
Using Pythagoras theorem,
𝐻𝑦𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑒2
= 𝐴𝑑𝑗𝑎𝑐𝑒𝑛𝑡2
+ (𝑂𝑝𝑝𝑜𝑠𝑖𝑡𝑒2
)
22
= 12
+ (ℎ2
)
ℎ = 3
𝑆𝑖𝑛 30° =
1
2
𝑆𝑖𝑛 60° =
3
2
𝐶𝑜𝑠 30° =
3
2
𝐶𝑜𝑠 60° =
1
2
tan 30° =
1
3
tan 60° =
3
1
3
6

16. Trigonometric Ratios of Some Specific Angles
› To find out trigonometric ratios of 45° we consider an
isosceles right triangle and proceed.

17. TRIGONOMETRIC
RATIOS OF SOME
SPECIFIC ANGLES
TIPS:
1. Cos 𝜃 will be reverse
order of Sin 𝜃.
2. tan 𝜃 will be sin 𝜃 divided
by cos 𝜃.
3. Cosec 𝜃, sec 𝜃 and cot
𝜃 will be reciprocal of sin
𝜃, cos 𝜃 and tan
𝜃 respectively.
REMEMBER only for Sin.

18. Trigonometry
Unit 6 – Part 2

19. Content
› Trigonometric Identities
› Heights and distance- Application of Trigonometry

20. Three Fundamental Identities of Trigonometry
Proof:
In the right angled ΔOMP
𝑂𝑀
𝑂𝑃
= Cos 𝜃 and
𝑃𝑀
𝑂𝑃
= Sin 𝜃---------(1)
By Pythagoras theorem
𝑀𝑃2 + 𝑂𝑀2 = 𝑂𝑃2-------------------(2)
Dividing each term on both sides by
OP2
𝑀𝑃
𝑂𝑃
2
+
𝑂𝑀
𝑂𝑃
2
=
𝑂𝑃
𝑂𝑃
2
From (1), Cos2𝜃 + Sin2𝜃 = 12
Hence, Cos2𝜃 + Sin2𝜃 = 1
Proof:
In the right angled ΔOMP,
𝑀𝑃
𝑂𝑃
= tan 𝜃 and
𝑂𝑃
𝑂𝑀
= Sec 𝜃---------(3)
From (2), 𝑀𝑃2
+ 𝑂𝑀2
= 𝑂𝑃2
Dividing each term on both sides by
OM2,
𝑀𝑃
𝑂𝑀
2
+
𝑂𝑀
𝑂𝑀
2
=
𝑂𝑃
𝑂𝑀
2
From (3), 12
+tanΘ2= 𝑠𝑒𝑐𝜃2
Hence, 1+tanΘ2= 𝑠𝑒𝑐𝜃2

21. PROBLEM 1
sin𝜃(1+ 𝑠𝑖𝑛2
𝜃) = 𝑐𝑜𝑠2
𝜃
Square both sides
sin2𝜃 (1+ 𝑠𝑖𝑛2
𝜃)2 = 𝑐𝑜𝑠4
𝜃
Now substitute
(1- Cos2𝜃) (1+1- Cos2𝜃)2 = 𝑐𝑜𝑠4
𝜃
(1- Cos2𝜃) (2- Cos2𝜃)2 = 𝑐𝑜𝑠4 𝜃
Using: (a-b)2 =a2+b2-2ab
(1- Cos2𝜃) (4+Cos4𝜃-4Cos2𝜃) = 𝑐𝑜𝑠4 𝜃
4+Cos4𝜃-4Cos2𝜃–4Cos2𝜃–Cos6𝜃+ 4Cos4
𝜃 = Cos4𝜃
On simplifying
𝑐𝑜𝑠6
𝜃−4 𝑐𝑜𝑠4
𝜃+ 8 𝑐𝑜𝑠2
𝜃= 4
If sin𝜃(1+ 𝑠𝑖𝑛2 𝜃) = 𝑐𝑜𝑠2 𝜃 ,
then prove that 𝑐𝑜𝑠6
𝜃−4
𝑐𝑜𝑠4 𝜃+ 8 𝑐𝑜𝑠2 𝜃= 4

22. PROBLEM 2
Prove the following identity

23. PROBLEM 3:

24. Heights and Distances
› Trigonometry can be used for finding the heights and
distances of various objects without actually measuring
them. For example, the height of a tower, mountain,
building or tree, distance of a ship from a light house,
width of a river, etc.
› The process of finding Heights and Distances is the best
example of applying trigonometry in real-life situations.

25. Terminologies in Heights and distances
› Line of Sight: The line of sight is
the line drawn from the eye of an
observer to the point in the object
viewed by the observer.
› Angle of Elevation: The angle of
elevation is an angle formed by the
line of sight with the horizontal
when the point being viewed is
above the horizontal level.
› Angle of Depression: The angle of
depression is an angle formed by
the line of sight with the horizontal
when the point is below the
horizontal level.

26. PROBLEM 1:
ELEVATION
A
B
D
C 7 m 5 m
h
r
45°
30°
E
r
In ∆ ABC
tan 45°=
𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒
𝐴𝑑𝑗𝑎𝑐𝑒𝑛𝑡
=
ℎ+𝑟
𝑟+7
= 1
h + r = r+7
h=7 m
In ∆EDC
tan 30°=
𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒
𝐴𝑑𝑗𝑎𝑐𝑒𝑛𝑡
=
𝑟
𝑟+7+5
=
1
3
3𝑟 = 12 + 𝑟
1.732 r- r =12
0.732 r = 12
r= 16.39 m

27. PROBLEM 2:
DEPRESSION
tan 30°=
𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒
𝐴𝑑𝑗𝑎𝑐𝑒𝑛𝑡
=
ℎ
𝑥
=
1
3
3ℎ =x
tan 60°=
𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒
𝐴𝑑𝑗𝑎𝑐𝑒𝑛𝑡
=
ℎ
𝑦
=
3
1
3𝑦 =h
The distance between ships = x+y
= 3ℎ+
ℎ
3
From the top of a
lighthouse, the angle of
depression of two ships on
the opposite sides of it are
observed to be 30° and
60°. If the height of the
lighthouse is h meters and
the line joining the ships
passes through the foot of
the lighthouse, show that
the distance between the
ships is 4h/√3 m.
4h/√3 m
30° 60°
30° 60°
h
y
x

28. PROBLEM 3
ELEVATION
& DEPRESSION
tan 20°=
𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒
𝐴𝑑𝑗𝑎𝑐𝑒𝑛𝑡
=
𝐸𝐵
8
= 0.3640
EB= vertical height between A and
B= 8*0.3640 = 2.912 Km
tan 30°=
𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒
𝐴𝑑𝑗𝑎𝑐𝑒𝑛𝑡
=
𝐶𝐷
12
=
1
3
CD = vertical height between B and
C= 12/ 3 = 6.928 Km
C
E
D
B
A
20°
30°
12 Km
8 Km
8 Km

29. PROBLEM 4: An observer 1.5 m tall is 20.5 m away
from a tower 22 m high. Determine the angle of
elevation of the top of the tower from the eye of the
observer.