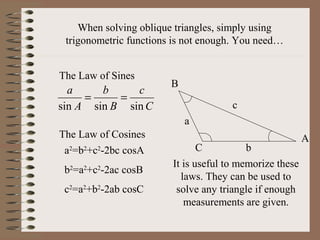
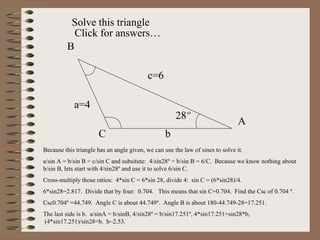
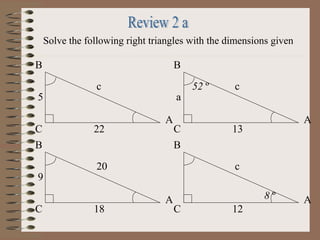
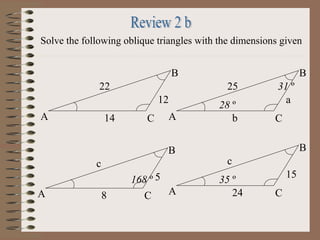
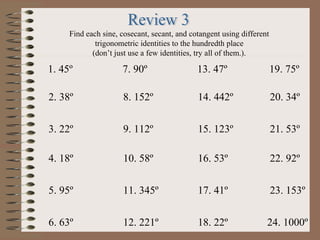
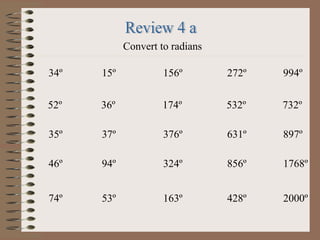
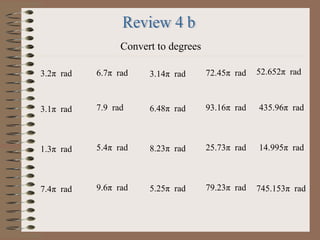
This PowerPoint presentation covers trigonometry and solving triangles using trigonometric functions and identities. It introduces trigonometric ratios like sine, cosine, and tangent and how they are used to solve right triangles. It then covers solving both right and oblique triangles using the Law of Sines and Law of Cosines. The presentation also discusses trigonometric identities and conversions between degrees and radians. Examples are provided to demonstrate solving triangles using the concepts introduced.

1. A mathematics PowerPoint
by Eric Zhao

2. Trigonometry is the study and solution of
Triangles. Solving a triangle means finding
the value of each of its sides and angles. The
following terminology and tactics will be
important in the solving of triangles.
Pythagorean Theorem (a2
+b2
=c2
). Only for right angle triangles
Sine (sin), Cosecant (csc or sin-1
)
Cosine (cos), Secant (sec or cos-1
)
Tangent (tan), Cotangent (cot or tan-1
)
Right/Oblique triangle

4. A trigonometric function is a ratio of certain parts of a triangle. The
names of these ratios are: The sine, cosine, tangent, cosecant, secant,
cotangent.
Let us look at this triangle…
a
c
b
ө A
B
C
Given the assigned letters to the sides and
angles, we can determine the following
trigonometric functions.
The Cosecant is the inversion of the
sine, the secant is the inversion of
the cosine, the cotangent is the
inversion of the tangent.
With this, we can find the sine of the
value of angle A by dividing side a
by side c. In order to find the angle
itself, we must take the sine of the
angle and invert it (in other words,
find the cosecant of the sine of the
angle).
Sinθ=
Cos θ=
Tan θ=
Side Opposite
Side Adjacent
Side Adjacent
Side Opposite
Hypothenuse
Hypothenuse
=
=
= a
b
c
a
b
c

5. Try finding the angles of the following triangle from the
side lengths using the trigonometric ratios from the
previous slide.
6
10
8
θ A
B
C
α
β
Click for the Answer…
The first step is to use the trigonometric
functions on angle A.
Sin θ =6/10
Sin θ =0.6
Csc0.6~36.9
Angle A~36.9
Because all angles add up to 180,
B=90-11.537=53.1
C
2
34º A
B
α
β
The measurements have changed. Find side BA and side AC
Sin34=2/BA
0.559=2/BA
0.559BA=2
BA=2/0.559
BA~3.578
The Pythagorean theorem when
used in this triangle states
that…
BC2
+AC2
=AB2
AC2
=AB2
-BC2
AC2
=12.802-4=8.802
AC=8.8020.5
~3

7. When solving oblique triangles, simply using
trigonometric functions is not enough. You need…
The Law of Sines
C
c
B
b
A
a
sinsinsin
==
The Law of Cosines
a2
=b2
+c2
-2bc cosA
b2
=a2
+c2
-2ac cosB
c2
=a2
+b2
-2ab cosC
It is useful to memorize these
laws. They can be used to
solve any triangle if enough
measurements are given.
a
c
b
A
B
C

8. When solving a triangle, you must remember to choose
the correct law to solve it with.
Whenever possible, the law of sines should be used.
Remember that at least one angle measurement must be
given in order to use the law of sines.
The law of cosines in much more difficult and time
consuming method than the law of sines and is harder to
memorize. This law, however, is the only way to solve a
triangle in which all sides but no angles are given.
Only triangles with all sides, an angle and two sides, or a
side and two angles given can be solved.

9. a=4
c=6
b
A
B
C
28º
Solve this triangle
Click for answers…
Because this triangle has an angle given, we can use the law of sines to solve it.
a/sin A = b/sin B = c/sin C and subsitute: 4/sin28º = b/sin B = 6/C. Because we know nothing about
b/sin B, lets start with 4/sin28º and use it to solve 6/sin C.
Cross-multiply those ratios: 4*sin C = 6*sin 28, divide 4: sin C = (6*sin28)/4.
6*sin28=2.817. Divide that by four: 0.704. This means that sin C=0.704. Find the Csc of 0.704 º.
Csc0.704º =44.749. Angle C is about 44.749º. Angle B is about 180-44.749-28=17.251.
The last side is b. a/sinA = b/sinB, 4/sin28º = b/sin17.251º, 4*sin17.251=sin28*b,
(4*sin17.251)/sin28=b. b~2.53.

10. a=2.4
c=5.2
b=3.5A
B
C
Solve this triangle:
Hint: use the law of cosines
Start with the law of cosines because there are no angles given.
a2
=b2
+c2
-2bc cosA. Substitute values. 2.42
=3.52
+5.22
-2(3.5)(5.2) cosA,
5.76-12.25-27.04=-2(3.5)(5.2) cos A, 33.53=36.4cosA, 33.53/36.4=cos A, 0.921=cos A, A=67.07.
Now for B.
b2
=a2
+c2
-2ac cosB, (3.5)2
=(2.4)2
+(5.2)2
-2(2.4)(5.2) cosB, 12.25=5.76+27.04-24.96 cos B.
12.25=5.76+27.04-24.96 cos B, 12.25-5.76-27.04=-24.96 cos B. 20.54/24.96=cos B. 0.823=cos B.
B=34.61.
C=180-34.61-67.07=78.32.

12. Trigonometric identities are ratios
and relationships between certain
trigonometric functions.
In the following few slides, you
will learn about different
trigonometric identities that take
place in each trigonometric
function.

13. What is the sine of 60º? 0.866. What is the cosine of 30º?
0.866. If you look at the name of cosine, you can actually
see that it is the cofunction of the sine (co-sine). The
cotangent is the cofunction of the tangent (co-tangent), and
the cosecant is the cofunction of the secant (co-secant).
Sine60º=Cosine30º
Secant60º=Cosecant30º
tangent30º=cotangent60º

14. Sin θ=1/csc θ
Cos θ=1/sec θ
Tan θ=1/cot θ
Csc θ=1/sin θ
Sec θ=1/cos θ
Tan θ=1/cot θ
The following trigonometric identities are useful to remember.
(sin θ)2
+ (cos θ)2
=1
1+(tan θ)2
=(sec θ)2
1+(cot θ)2
=(csc θ)2

16. Degrees and pi radians are two methods of
showing trigonometric info. To convert
between them, use the following equation.
2π radians = 360 degrees
1π radians= 180 degrees
Convert 500 degrees into radians.
2π radians = 360 degrees, 1 degree = 1π radians/180,
500 degrees = π radians/180 * 500
500 degrees = 25π radians/9

18. Write out the each of the trigonometric functions (sin, cos, and tan) of the following
degrees to the hundredth place.
(In degrees mode). Note: you do not have to do all of them 
1. 45º
2. 38º
3. 22º
4. 18º
5. 95º
6. 63º
7. 90º
8. 152º
9. 112º
10. 58º
11. 345º
12. 221º
13. 47º
14. 442º
15. 123º
16. 53º
17. 41º
18. 22º
19. 75º
20. 34º
21. 53º
22. 92º
23. 153º
24. 1000º

19. Solve the following right triangles with the dimensions given
5
c
22
A
B
C
9
20
18
A
B
C
A
a
c
13
B
C
52 º
c
12
8 º A
B
C

20. Solve the following oblique triangles with the dimensions given
12
22
14A
B
C
a
25
b
28 º
A
B
C
31 º
15
c
24
35 º
A
B
C
5
c
8A
B
C
168 º

21. 1. 45º
2. 38º
3. 22º
4. 18º
5. 95º
6. 63º
7. 90º
8. 152º
9. 112º
10. 58º
11. 345º
12. 221º
13. 47º
14. 442º
15. 123º
16. 53º
17. 41º
18. 22º
19. 75º
20. 34º
21. 53º
22. 92º
23. 153º
24. 1000º
Find each sine, cosecant, secant, and cotangent using different
trigonometric identities to the hundredth place
(don’t just use a few identities, try all of them.).

22. Convert to radians
52º
34º
35º
46º
74º
36º
15º
37º
94º
53º
174º
156º
376º
324º
163º
532º
272º
631º
856º
428º
732º
994º
897º
1768º
2000º

23. Convert to degrees
3.2π rad
3.1π rad
1.3π rad
7.4π rad
6.7π rad
7.9 rad
5.4π rad
9.6π rad
3.14π rad
6.48π rad
8.23π rad
5.25π rad
72.45π rad
93.16π rad
25.73π rad
79.23π rad
52.652π rad
435.96π rad
14.995π rad
745.153π rad

24. Creator
Eric Zhao
Director
Eric Zhao
Producer
Eric Zhao
Author
Eric ZhaoMathPower Nine, chapter 6Basic Mathematics Second edition
By Haym Kruglak, John T. Moore, Ramon Mata-Toledo