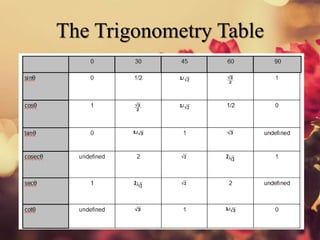
Trigonometry deals with triangles and the angles between sides. The main trigonometric ratios are defined using the sides of a right triangle: sine, cosine, and tangent. Trigonometric functions can convert between degrees and radians. Standard angle positions and trigonometric identities relate trig functions of summed and subtracted angles. The sine and cosine rules relate the sides and angles of any triangle, allowing for calculations of missing sides or angles given other information. Unit circle graphs further illustrate trigonometric functions.

1. Trigonometry

2. WHAT IS TRIGNOMETRY
• Trigonometry is a branch of mathematics
which deals with triangles and their
slides and the angles between these
slides.
• Word tri means three ,gon means sides
and metron means measure

3. Trigonometric Ratios
In this right angle triangle,
• the trigonometric ratios of angle
A in right angle ABC are:
• Sin A-side opp.to angle A/Hypotenus-BC/AC.
• Cos A-adjacent of angle A/hypotenus-AB/AC.
• Tan A-opp. Of angle A/adjacent-BC/AB.
• Cosec A- AC/BC(OPPOSITE OF SIN).
• Sec-AC/AB(OPPOSITE OF COS).
• COT-AB/BC(OPPOSITE OF TAN).

4. The Trigonometry Table

5. Conversion of Angles
• There are two systems of measurements of
angles i.e., degree and radian.
• Conversion of degree to radian;-)
Radian=DEGREE*(^/180)
• Conversion of radian to degree;-)
DEGREE=RADIAN*(180/^)

6. Angles in standard position

7. A-B Formula
sin(A+B)=sin A cos B + cos A sin B
sin(A-B)=sin A cos B - cos A sin B
cos(A+B)=cos A cos B - sin A sin B
cos(A-B)=cos A cos B + sin A sin B

8. SINE AND COSINE RULE-
• The sine and cosine rules relate the sides and angles in
any triangle.
• Consider a triangle ABC where a = BC, b = AC and c =
AB.
• If you are given the lengths of any two sides a and b
and the angle C between those two sides (the included
angle), then you can use the cosine rule to calculate
the length of the remaining side c: . A specific case of
this is the Pythagoras' theorem for right-angled
triangles, where C = π/2 radians or 90 degrees, then .
• If you are given the lengths of all three sides a, b and c,
then you can use the cosine rule to calculate any angle
within the triangle; for angle C this is: .

9. CONTINUE…
• If you are given any two angles A and B and the
length a side not in between these two angles -
either a or b, then you can use the sine rule to
calculate one of the missing sides: .
• If you are given the lengths of any two sides a and b,
and the angle A or B that is not in between the two
sides, then this is known as the ambiguous case as
the sine rule: will result in two possible sizes for one
of the missing angles: . In this case, determine which
one of the angles is not possible from the
information given in the question.
• The area of any triangle, given the lengths of any
two sides a and b and the included angle C, is:

10. FROM SINE/COSINE UNIT GRAPH

11. Bibliography
o Images-
http://jwilson.coe.uga.edu/emt668/EMAT668
0.2002.Fall/Wright/6690/lesson%203/lesson%
203.html
o Contents-ibid mathematics hl core 4th edition

12. .
Thank u
ppt made by-
Tarun Sharma