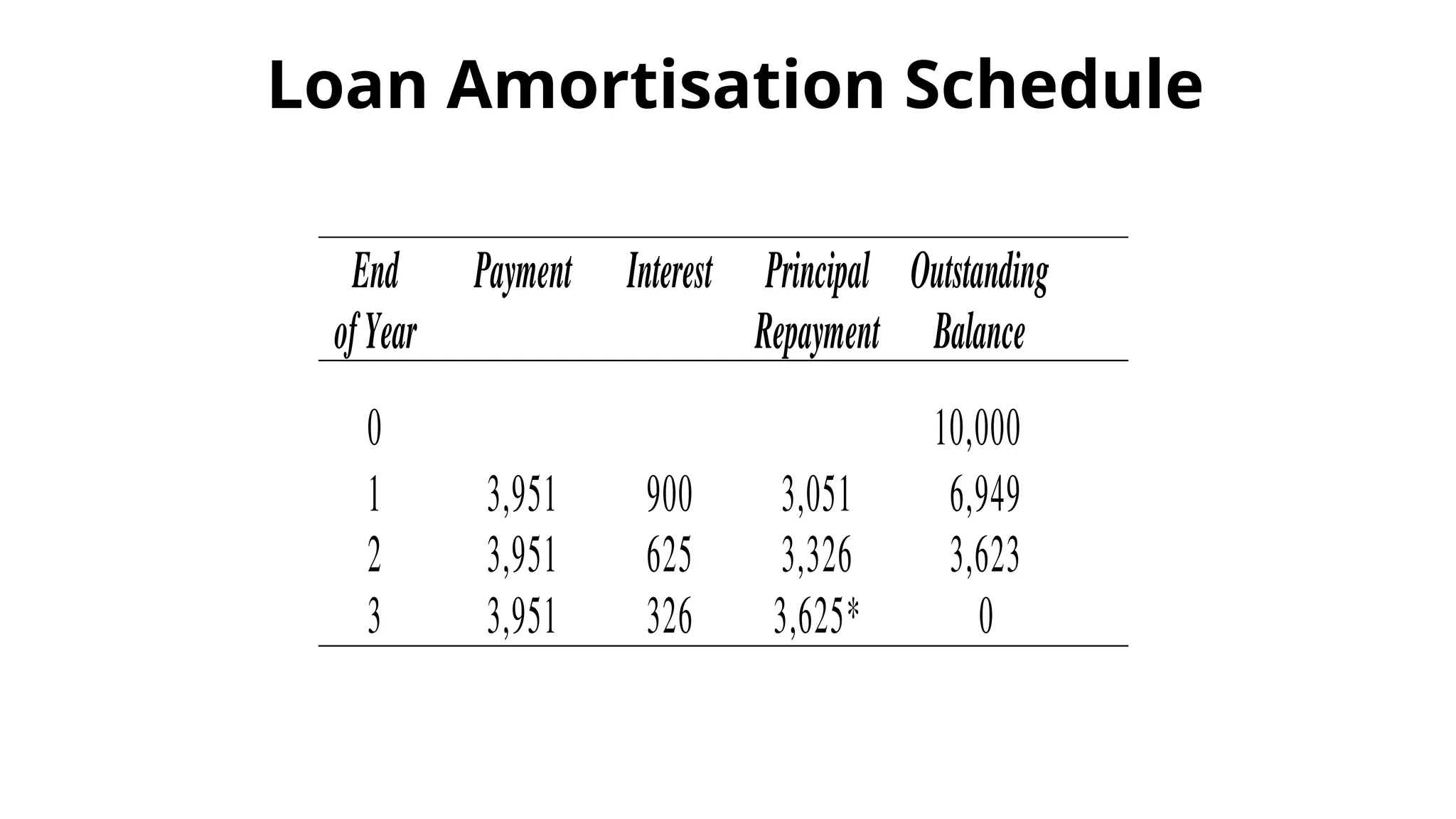
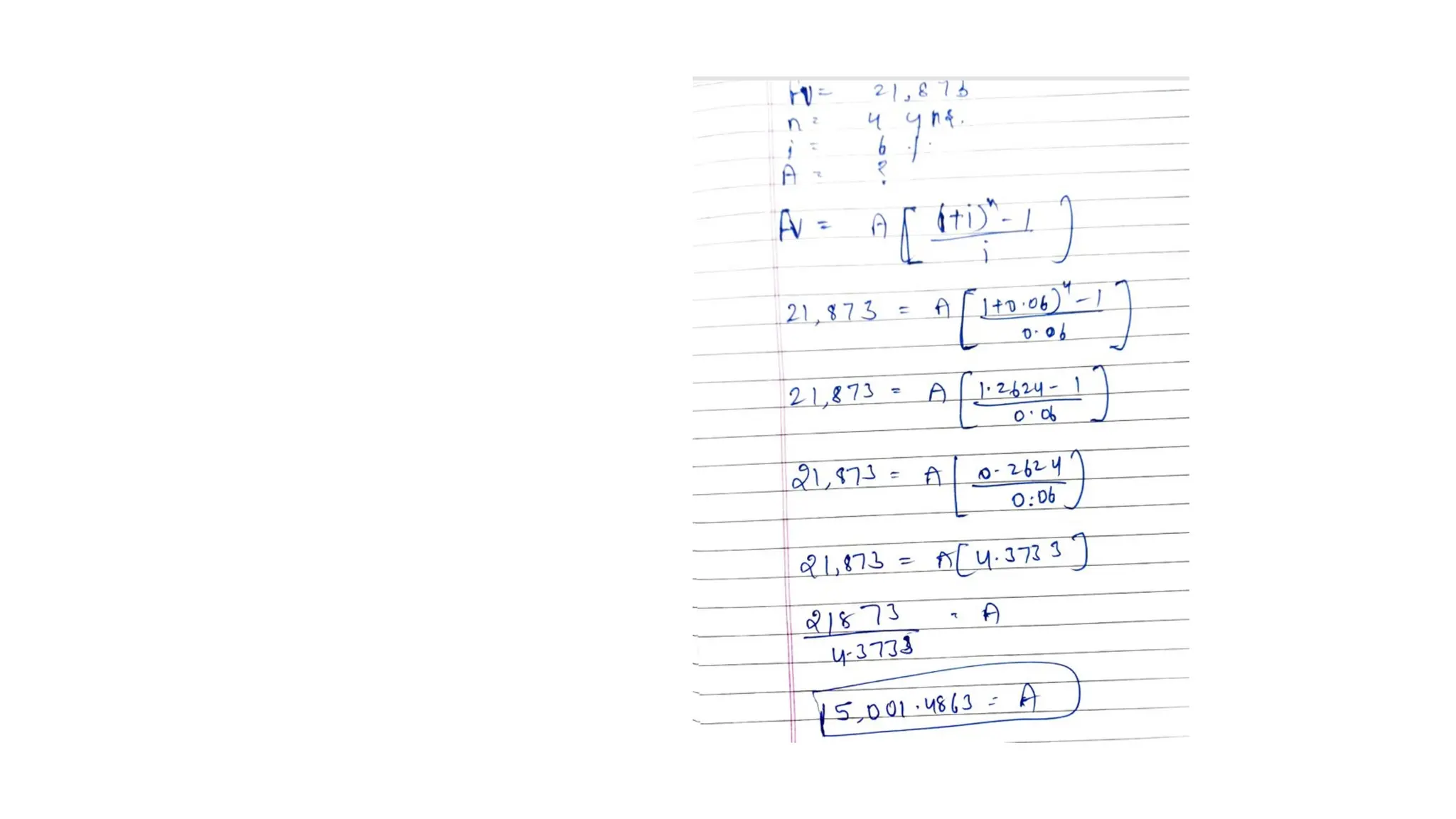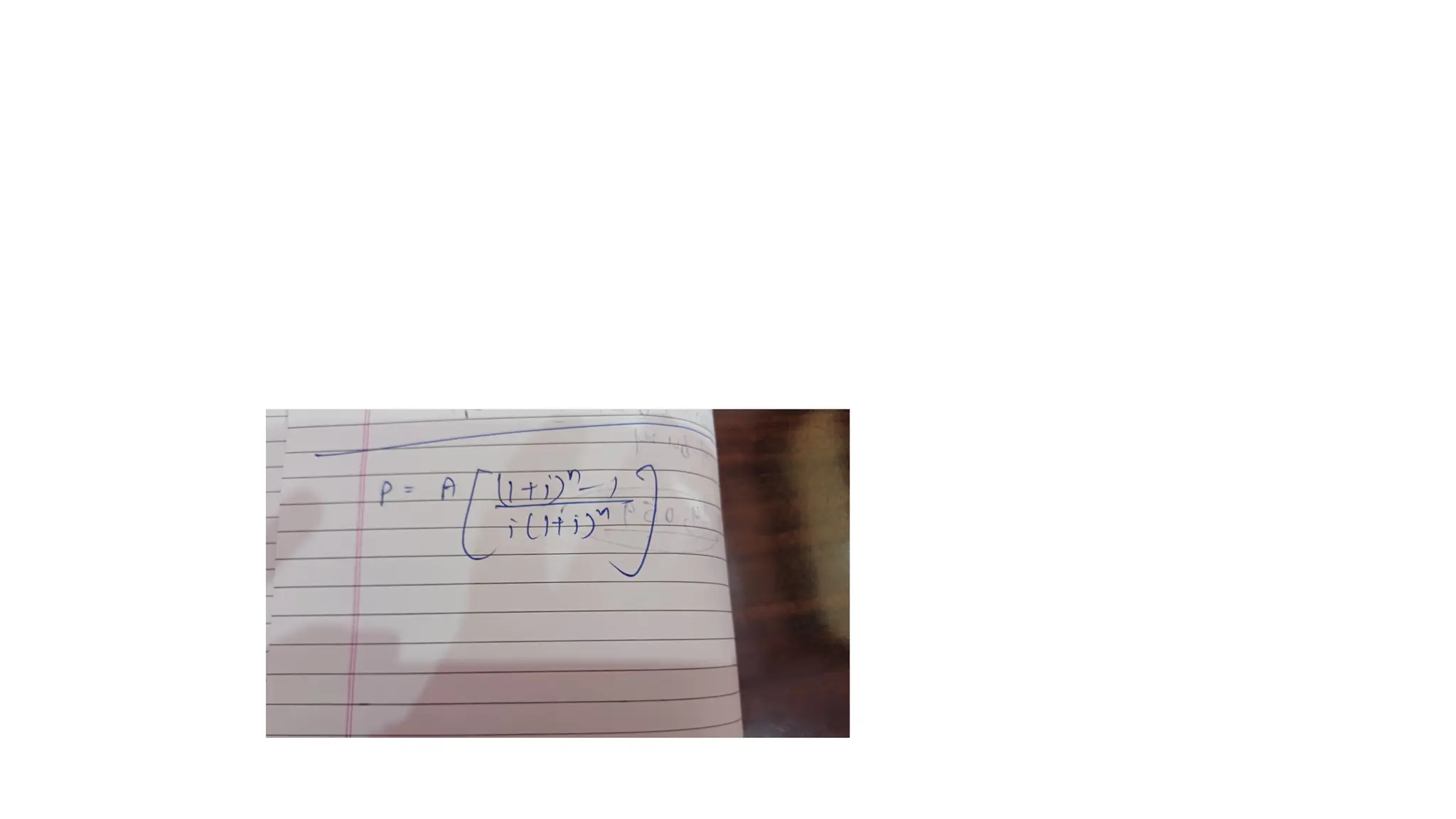The document explains the concept of the time value of money, detailing how present and future values are calculated and the importance of adjusting cash flows for time and risk. It introduces key concepts like time preference for money, required rate of return, and methods such as compounding and discounting. Real-world examples illustrate these principles, including future and present value calculations, annuities, and internal rate of return.

1. Time Value of Money

2. LEARNING OBJECTIVES
• Understand what gives money its time value.
• Explain the methods of calculating present and future
values.
• Highlight the use of present value technique (discounting) in
financial decisions.
• Introduce the concept of internal rate of return.

3. Time Preference for Money
• Time preference for money is an individual’s preference for
possession of a given amount of money now, rather than
the same amount at some future time.
• Three reasons may be attributed to the individual’s time
preference for money:
• risk
• preference for consumption
• investment opportunities

4. Required Rate of Return
• The time preference for money is generally expressed by an
interest rate. This rate will be positive even in the absence of
any risk. It may be therefore called the risk-free rate.
• An investor requires compensation for assuming risk, which
is called risk premium.
• The investor’s required rate of return is:
Risk-free rate + Risk premium.

5. Required Rate of Return
• Would an investor want Rs. 100 today or after one year?
• Cash flows occurring in different time periods are not comparable.
• It is necessary to adjust cash flows for their differences in timing and risk.
• Example : If preference rate =10 percent
• An investor can invest if Rs. 100 if he is offered Rs 110 after one year.
• Rs 110 is the future value of Rs 100 today at 10% interest rate.
• Also, Rs 100 today is the present value of Rs 110 after a year at 10% interest rate.
• If the investor gets less than Rs. 110 then he will not invest. Anything above Rs.
110 is favourable.

6. Time Value Adjustment
• Two most common methods of adjusting cash flows for time
value of money:
• Compounding—the process of calculating future values of cash
flows and
• Discounting—the process of calculating present values of cash
flows.

7. Future Value
• Compounding is the process of finding the future values of
cash flows by applying the concept of compound interest.
• Compound interest is the interest that is received on the
original amount (principal) as well as on any interest earned
but not withdrawn during earlier periods.
• Simple interest is the interest that is calculated only on the
original amount (principal), and thus, no compounding of
interest takes place.

8. Future Value
8

9. • 1) FV calculation of Lump sum
• Invested 50,000 for 4 years – Fixed deposit
• 2) FV calculation of Annuity
• Invested 10,000 every year for 4 years.

10. • In Microsoft Excel: Use FV function.
FV(rate,nper,pmt,pv,type)
Where: rate= interest rate. nper= n periods, pmt= annuity
value, pv= present value, type= 1 for beginning of the period
and 0 for end for end of period.

11. Future Value: Example

14. • P = Rs. 55,650
• i=15%
• n=10 years
• F = ? (To find)
• F = P(1+i)pow(n)
• F = 55,650 x (1+0.15)pow 10
• F = 55,650 x 4.0455
• F = Rs. 2,25,132

15. • Q: Suppose that `1,000 are placed in the savings account of
a bank at 5 per cent interest rate. How much shall it grow at
the end of three years

16. Solution

17. Future Value of an Annuity

18. Future Value of an Annuity: Example

19. • A = Rs 5,000
• n=4 years
• i=6%
• F=P (1+i) pow (n)
• F = 5000(1+0.06) pow (1)

20. Solution

22. Sinking Fund

23. • F = 10 lacs
• N = 15 years
• i=9%
• A = ??
• A = 34,059

24. Question
• Suppose we want to accumulate `21,873 at the end of four
years from now. How much should we deposit each year at
an interest rate of 6 per cent so that it grows to `21,873 at
the end of fourth year?

25. Solution

26. Example

27. Present Value
• Present value of a future cash flow (inflow or outflow) is the
amount of current cash that is of equivalent value to the
decision-maker.
• Discounting is the process of determining present value of
a series of future cash flows.
• The interest rate used for discounting cash flows is also
called the discount rate.

28. Present Value of a Single Cash Flow

29. • F = P(1+i) pow (n)

30. Example

31. Present Value of an Annuity

33. Example
33

34. Capital Recovery and Loan
Amortisation
34

35. Loan Amortisation Schedule
35
End Payment Interest Principal Outstanding
ofYear Repayment Balance
0 10,000
1 3,951 900 3,051 6,949
2 3,951 625 3,326 3,623
3 3,951 326 3,625* 0

36. Present Value of an Uneven Periodic
Sum
• In most instances the firm receives a stream
of uneven cash flows. Thus the present value
factors for an annuity cannot be used.
• The procedure is to calculate the present
value of each cash flow and aggregate all
present values.
36

37. PV of Uneven Cash Flows: Example
37

38. • Year 2025
• After 1 year (2026) = 1000
• Aftwer 2 years (2027) = 1500
• After 3 years (2028) = 800
• After 4 years (2029) = 1100
• After 5 years (2030) = 400
• What is the Present worth of the stream of cash flows.

39. • F = 1500
• I = 8%
• N=2
• P =

40. Present Value of Perpetuity
40

41. Present Value of a Perpetuity:
Example
41

42. Present Value of Growing Annuities
42

43. PV of growing annuity
• A = 1000
• g=5% per annum
• i=9% per annum
• N=8 years
• P = 6,465
• P = A/i-g

44. Example
44

45. Example
45

46. Value of an Annuity Due
46

47. Future Value of An Annuity: Example
47

48. Example
• The present value of Re 1 paid at the
beginning of each year for 4 years is
1 × 3.170 × 1.10 = Rs 3.487
48

49. Multi-Period Compounding
49

50. Effective Interest Rate:
Example
50

51. Continuous Compounding
51

52. Net Present Value
52

53. Present Value and Rate of
Return
• A bond that pays some specified amount in future
(without periodic interest) in exchange for the current
price today is called a zero-interest bond or zero-
coupon bond.
• In such situations, one would be interested to know
what rate of interest the advertiser is offering. One
can use the concept of present value to find out the
rate of return or yield of these offers.
• The rate of return of an investment is called internal
rate of return since it depends exclusively on the
cash flows of the investment.
53

54. Internal Rate of Return
54

55. IRR Calculation: Example of Trial-Error
Method
55