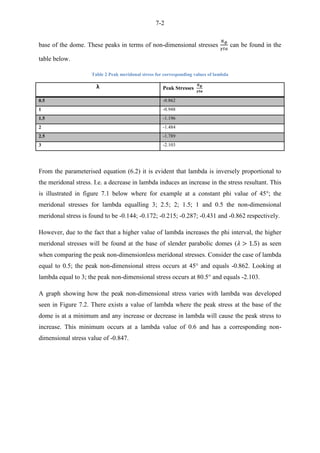
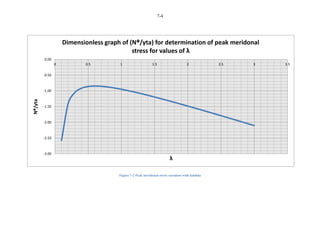
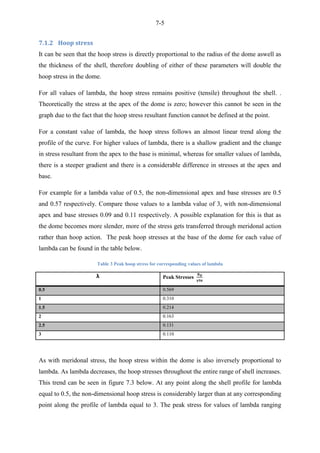
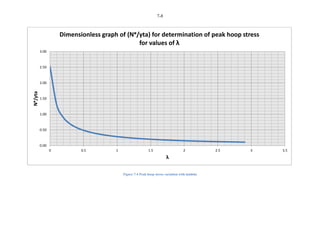
This document presents an undergraduate thesis analyzing the stress distribution in parabolic and ellipsoidal concrete domes. The student, Nazeer Slarmie, conducted a literature review on shell structures and shell theory. Slarmie then developed closed form solutions to determine the membrane stress equations for a parabolic dome of revolution and attempted to do the same for an ellipsoidal dome of revolution through a method of sections.






















![2-9
1 (2.1) General meridonal stress equation
N [∫ ( ) ]. (2.1)
2 (2.1) General hoop stress equation
(2.1)
This equation shows that the hoop stress is a function of meridonal stress, geometric
properties as well as the loading.
2.3.3 Deformation of Shells
The equations for the displacement of a spherical dome under axisymmetric loading were
determined by using the hoop and meridonal stresses found above. These displacements were
initially in the hoop and meridonal direction, however that for the sake of practicality, the
equations were developed such that the horizontal shell displacement as well as the rotation
of the meridian (δ and V respectively) can be calculated.
(N N ) (2.3)
* N – N (N N ) + (2.4)
2.4 Membrane analysis of concrete domes of revolution
The membrane field of internal forces comprises of the meridonal, hoop and a membrane
shear force. However, under axisymmetric loading conditions, the membrane shear force is
zero throughout the shell and the internal force field comprises of meridonal and hoop forces
only. The directions of principal normal stresses coincide with meridonal and hoop curve and
the shear stress will be zero along these directions.](https://image.slidesharecdn.com/4d589dfb-0192-4406-b7cb-91f9657402c7-161027121742/85/Thesis-2012-23-320.jpg)