La tesi di laurea di Giorgio Crasto, sotto la supervisione del prof. Natolino Mandas, esplora la simulazione dello strato limite atmosferico (SLA) su terreni con specifica orografia, focalizzandosi sulla collinetta di Askervein in Scozia. Viene fornita un'analisi dettagliata della fisica del SLA e delle metodologie di simulazione, inclusi i modelli di turbolenza e le impostazioni per le simulazioni 2D e 3D. Il lavoro è finalizzato a valutare il potenziale energetico eolico in base alla propagazione del SLA, contribuendo alla scelta ottimale per il posizionamento di turbine eoliche.

1. UNIVERSITA’ DEGLI STUDI DI CAGLIARI
FACOLTA’ DI INGEGNERIA
DIPARTIMENTO DI INGEGNERIA MECCANICA
Simulazioni della evoluzione dello SLA
(Strato Limite Atmosferico) su terreni dalla
orografia assegnata.
Relatore:
Prof. Ing. Natalino Mandas
Tesi di laurea di:
Giorgio Crasto
Correlatore:
Dott. Ing. Francesco Cambuli
ANNO ACCADEMICO 2002–2003

2. II
Ai miei genitori

3. III
Indice
Indice III
Ringraziamenti...................................................................................................................................VI
Nomenclatura ................................................................................................................................... VII
CAPITOLO 1 LO STRATO LIMITE ATMOSFERICO............................. 1
1.1 Introduzione. .......................................................................................................................... 1
1.2 Lo Strato Limite Atmosferico............................................................................................... 2
1.3 Statica dell’atmosfera............................................................................................................ 4
1.3.1 L’aria umida atmosferica................................................................................................ 4
1.3.2 Il gradiente verticale di temperatura e l’atmosfera politropica....................................... 5
1.3.3 La stabilità atmosferica. ................................................................................................. 5
1.4 Lo strato limite turbolento, flusso su pareti lisce. ............................................................... 9
1.4.1 Sottostrato Viscoso....................................................................................................... 10
1.4.2 Strato esterno................................................................................................................ 11
1.5 Effetto della rugosità delle pareti sullo strato limite turbolento...................................... 12
1.6 Effetto della stabilità atmosferica sul profilo di velocità del vento.................................. 16
1.7 La legge logaritmica modificata.......................................................................................... 18
1.8 Il vento alla Ekman.............................................................................................................. 18
1.9 Legge di resistenza geostrofica ed il vento geostrofico...................................................... 20
CAPITOLO 2 IMPOSTAZIONI PER LE SIMULAZIONI........................ 22
2.1 Le equazioni generali del moto. .......................................................................................... 22
2.2 La turbolenza. Modello di turbolenza utilizzato. .............................................................. 23
2.3 Il metodo numerico di risoluzione delle equazioni del moto. Discretizzazione del
dominio di calcolo e delle equazioni del modello............................................................... 26
2.4 Definizione delle caratteristiche fisiche dei materiali, fluidi e solidi, considerati nelle
simulazioni............................................................................................................................ 29
2.5 Valutazione del flusso a ridosso delle pareti. Flusso su superfici lisce. ........................... 33
2.5.1 Standard Wall Functions. ............................................................................................. 34

4. IV
2.5.2 Non-equilibrium wall functions. .................................................................................. 34
2.5.3 Two-Layer zonal model. .............................................................................................. 35
2.6 Valutazione del flusso a ridosso delle pareti. Flusso su superfici rugose......................... 35
2.7 Costruzione della griglia in prossimità delle pareti. ......................................................... 37
2.8 Scelta delle costanti del modello di turbolenza standard k-εεεε. ........................................... 42
2.9 Flusso su terreni pianeggianti............................................................................................. 43
2.9.1 Discretizzazione del dominio di calcolo e condizioni al contorno. .............................. 43
2.9.2 Profili in ingresso, andamento di alcune grandezze con la quota................................. 47
2.10 Condizioni operative............................................................................................................ 48
2.11 Risultati numerici delle simulazioni su superfici piane. ................................................... 49
2.12 Considerazioni sulla densità operativa............................................................................... 56
CAPITOLO 3 SIMULAZIONI 2D SULLA COLLINA DI ASKERVEIN... 57
3.1 Vento sopra terreni collinari............................................................................................... 57
3.2 Il progetto Askervein (The Askervein Hill Project)............................................................ 59
3.3 Costruzione della geometria bidimensionale..................................................................... 64
3.4 Le simulazioni 2D sulla collina di Askervein..................................................................... 66
3.4.1 Geometria e griglia....................................................................................................... 66
3.4.2 Condizioni al contorno. ................................................................................................ 67
3.4.3 Condizioni operative. ................................................................................................... 69
3.4.4 Scelta delle costanti caratteristiche del modello di turbolenza standard k-ε................ 70
3.4.5 Risultati numerici. ........................................................................................................ 70
CAPITOLO 4 SIMULAZIONI 3D SULLA COLLINA DI ASKERVEIN... 74
4.1 Geometria. Costruzione del dominio di calcolo................................................................. 74
4.2 Griglia. .................................................................................................................................. 81
4.3 Impostazioni delle simulazioni............................................................................................ 83
4.4 Elaborazione grafica dei risultati. ...................................................................................... 83
4.5 Calcolo della densità di energia. ......................................................................................... 89
Conclusioni. ........................................................................................................................................ 92

5. V
Appendice I – Costruzione dei file contenenti i profili in ingresso................................................. 94
Appendice II – Elaborazione dei file grd di terreni complessi. ...................................................... 95
Appendice III – Procedura seguita per i grafici di Capitolo 4. ...................................................... 97
Bibliografia. ........................................................................................................................................ 98

6. VI
Ringraziamenti
Questo lavoro non sarebbe stato possibile senza la collaborazione e la
disponibilità del Prof. Ing. N. Mandas e del Dott. Ing. F. Cambuli, della Università
degli Studi di Cagliari.
Desidero ringraziare il Dr. P. Taylor ed i suoi collaboratori Mr. W. Weng e Mr. J.
Walmsley, della University of York, Canada, per aver fornito le mappe digitalizzate
della collina di Askervein.
Sono stati di grande utilità il lavoro dell’Ing. J. Leroy e la tesi di PhD del Dr. G.
Eason, segnalati in bibliografia; li ringrazio in particolare per la scelta di rendere di
pubblico dominio i propri lavori.
Un ringraziamento va all’Ing. A. Caschili per il suo supporto tecnico.
Un ringraziamento particolare a mio padre, il Col. A. Crasto, del servizio
meteorologico dell’AM, che mi ha aiutato nell’approfondimento degli aspetti non
ingegneristici ma più prettamente fisici dell’argomento di tesi.

7. VII
Nomenclatura
Ah [m2
] area mediamente occupata da un ostacolo sulla parete (formula di
Lettau)
a0 [m-1
] grandezza di riferimento per il vento alla Ekman
cp [J/kg K] calore specifico a pressione costante dell’aria
cv [J/kg K] calore specifico a volume costante dell’aria
Cµ costante dei modelli k-ε
C1, C2, C3 costanti del modello standard k-ε
E costante del profilo di velocità del vento
e [J/kg] energia specifica
f [s-1
] parametro di Coriolis
Fx, Fy rapporto di velocità definite dalle (1.54) e (1.55)
g [m/s2
] accelerazione di gravità
Gk [kg/m s3
] produzione di energia cinetica turbolenta dovuta ai gradienti di
velocità
Gb [kg/m s3
] produzione di energia cinetica turbolenta dovuta alle forze di
galleggiamento
h [J/kg] entalpia
h [m] altezza media delle asperità di una parete
h [m] altezza di gradiente
h+
altezza delle asperità h adimensionalizzata con la velocità d’attrito
e la viscosità cinematica
h0 [J/kg] entalpia totale
H [m] altezza della collina misurata rispetto al territorio circostante
H0 [W/m kg] flusso di calore per unità di densità ed unità d’area
i [J/kg] energia interna
k [m2
/s2
] energia cinetica turbolenta, TKE (Turbulent Kinetic Energy)
KM [m2
/s] viscosità cinematica effettiva, ritenuta costante nel vento alla
Ekman
L [m] lunghezza di Monin-Obukhov
L [m] semi-ampiezza della collina, misurata a metà altezza nella
direzione di provenienza del vento

8. VIII
S [m] lunghezza di scala
[m] altezza alla quale si osserva il massimo incremento relativo di
velocità ∆S
m [kg] massa di aria contenuta nel volume V
mas [kg] massa di aria secca contenuta nel volume V
mV [kg] massa di vapore contenuta nel volume V
n, e, s, w punti medi dei segmenti P-N, P-E, P-S e P-W per una griglia 2D
N, E, S, W nodi adiacenti al nodo generico P per una griglia 2D
p [Pa] pressione
p0 [Pa] pressione al suolo
pas [Pa] pressione parziale dell’aria secca
pV [Pa] pressione parziale del vapore
pR [Pa] pressione di riferimento per la definizione della temperatura
potenziale, 1000 mbar
P nodo generico
Prt numero di Prandtl turbolento
q umidità specifica
R [J/kg K] costante specifica dell’aria umida
Ras [J/kg K] costante specifica dell’aria secca
RV [J/kg K] costante specifica del vapore
Ri numero di Richardson
Re* numero di Reynolds di rugosità (Roughness Reynolds number)
RH [m] Roughness Height, primo parametro usato da FLUENT per
descrivere la rugosità delle pareti
RH+
RH adimensionalizzato con la velocità d’attrito e la viscosità
cinematica
RC Roughness Constant, secondo parametro usato da FLUENT per
descrivere la rugosità delle pareti
S [m2
] superficie frontale dell’ostacolo nella formula di Lettau
S sorgente della grandezza generica φ per unità di volume, per unità
di tempo
S velocità normalizzata
SE [W/m3
] sorgente di energia per unità di volume, per unità di tempo
t [s] tempo
T [K] temperatura

9. IX
Tv [K] temperatura virtuale
T0 [K] temperatura al suolo
u, v, w [m/s] velocità istantanea in direzione x, y, z
U, V, W [m/s] componenti medie del vettore velocità
u', v’, w’ [m/s] componenti fluttuanti della velocità istantanea, in
direzione x, y, z
uw, u*, uτ [m/s] velocità d’attrito
u* gruppo adimensionale usato da FLUENT e definito dall’equazione
(2.23a)
u+
rapporto tra velocità media e velocità d’attrito
V [m3
] volume occupato dalla miscela aria umida
VS [m/s] velocità di scala
Vg [m/s] intensità del vento geostrofico
VH [m/s] velocità orizzontale media
x,y, z [m] coordinate cartesiane
y* gruppo adimensionale usato da FLUENT e definito dall’equazione
(2.23b)
y+
distanza y, normale alla parete, adimensionalizzata con densità,
velocità d’attrito e viscosità dinamica
z0 [m] lunghezza di rugosità
α angolo di rotazione del vento geostrofico rispetto al vento al suolo
β [Κ−1
] coefficiente di espansione termica
Γ [K/m] gradiente verticale di temperatura
Γ coefficiente di diffusione generico
Γad [K/m] gradiente adiabatico verticale di temperatura
δij delta di Kronecker
∆x, ∆y [m] dimensioni dell’area di controllo per discretizzare le equazioni di
conservazione attorno al nodo P
∆B funzione di rugosità (Roughness Function)
∆S incremento relativo di velocità
ε [m2
/s3
] velocità di dissipazione dell’energia cinetica turbolenta
(Turbulence Dissipation Rate o TDR)
ζ quota z adimensionalizzata con la lunghezza di Monin-Obukhov
θ [K] temperatura potenziale

10. X
θv [K] temperatura potenziale virtuale
θ’v [K] componente fluttuante della temperatura potenziale virtuale
λ [W/ m K] conducibilità termica
µ [Pa s] viscosità dinamica
µt [Pa s] viscosità dinamica turbolenta
µ parametro adimensionale di stabilità
υ [m2
/s] viscosità cinematica
ρ [kg/m3
] densità
ρ0 [kg/m3
] densità al suolo
σk numero di Prandtl turbolento per k (tke)
σε numero di Prandtl turbolento per ε (tdr)
τ [Pa] azione tangenziale
τw [Pa] azione tangenziale di parete
φ latitudine
φ grandezza generica
ψ(ζ) termine correttivo nella legge logaritmica che tiene conto della
stabilità termica
Ω [s-1
] velocità angolare di rotazione della Terra
Costanti
A ~2 costante della legge di resistenza geostrofica
B ~4,5 costante della legge di resistenza geostrofica
κ 0,42 costante di Von Karman
E 9,81 costante sperimentale
B 5,45
Grandezze vettoriali
F [m/s2
] forza per unità di massa
V [m/s] velocità

11. Capitolo 1 Lo Strato Limite Atmosferico.
1.1 Introduzione.
Le fonti rinnovabili di energia godono, in questi anni, di una particolare
attenzione, per la necessità di ridurre le emissioni nocive di sostanze inquinanti e gas
serra. L’Italia, in seguito alla sottoscrizione del protocollo di Kyoto, si è impegnata a
raggiungere nel giro di qualche anno una certa percentuale di produzione di energia
elettrica da fonti rinnovabili. Tale impegno dipende dall’anno di messa in esercizio
dei vari impianti, e, secondo le leggi vigenti attualmente, è regolata dal mercato dei
cosiddetti certificati verdi.
La legislazione corrente, in campo energetico, costringe i produttori di energia
elettrica a produrre una parte, se pur minima, a partire da fonti energetiche di tipo
rinnovabile.
Tra le fonti energetiche di maggiore interesse, per i rendimenti di conversione
ottenuti e per le ottime caratteristiche di rispetto per l’ambiente, è da citare l’energia
eolica, prodotta per mezzo di turbine eoliche a partire da una fonte energetica
perenne completamente pulita, il vento.
Tale risorsa gode di inevitabili vantaggi ma di un aspetto negativo fondamentale,
relativo alla sua disponibilità, in certi siti non sufficiente, dal punto di vista della
continuità e della intensità.
L’interesse verso la propagazione dello Strato Limite Atmosferico sui terreni reali
è dovuto alla necessità di valutare l’energia eolica estraibile in un dato sito. In
particolare, le simulazioni fluidodinamiche si propongono come strumento per
localizzare i posti più adatti al posizionamento degli aerogeneratori.
Il presente lavoro di tesi si inquadra nel programma di ricerca avviato dal
DIMECA sullo studio dello Strato Limite Atmosferico sui terreni di cui è nota
l’orografia.
Il lavoro presente si può suddividere in diverse sezioni. Nel primo capitolo
vengono illustrate alcune nozioni sulla fisica dello SLA. Il secondo capitolo è
dedicato alla descrizione di alcune caratteristiche del codice di calcolo ed alle
impostazioni utilizzate nelle simulazioni.
Nei capitoli terzo e quarto sono riportati i risultati delle simulazioni sulla
evoluzione dello SLA sopra la collina di Askervein, nelle isole Ebridi, in Scozia. Il
terzo capitolo concerne le simulazioni bidimensionali, il quarto capitolo quelle
tridimensionali.

12. 2
Si è scelto di studiare la propagazione dello SLA sulla collina di Askervein perché
sono disponibili in letteratura diversi dati anemometrici necessari per verificare
l’attendibilità delle simulazioni svolte.
Tutte le simulazioni effettuate nel presente lavoro sono state eseguite col codice di
calcolo FLUENT ed i domini di calcolo sono stati realizzati e discretizzati col pre-
processore GAMBIT, entrambi della FLUENT INC.
1.2 Lo Strato Limite Atmosferico.
Nello studio della dinamica dell’atmosfera si fa riferimento a diverse scale
dimensionali. Si analizzano, in genere, movimenti in scala piccola, media o grande.
Quando si parla di scala piccola i domini di studio hanno dimensioni di qualche
chilometro, in scala media le dimensioni orizzontali sono dell’ordine di qualche
centinaia di chilometri e possono comprendere, ad esempio, un’isola delle
dimensioni della Sardegna, mentre, quando si studia il movimento delle masse d’aria
in scala grande, detta anche sinottica, vengono considerati moti circolatori che
possono comprendere diversi stati o anche continenti.
Tutte le simulazioni numeriche portate avanti nel presente lavoro trattano studi in
piccola scala, e le dimensioni dei domini sono infatti qualche chilometro in
orizzontale e massimo due chilometri in verticale. In tale situazione si analizza quella
parte di atmosfera che interagisce direttamente col terreno nota come SLA.
Per Strato Limite Atmosferico (SLA), detto anche Strato Limite Planetario (SLP),
s’intende quella porzione di troposfera all’interno della quale avvengono tutte le
interazioni, o quasi, tra atmosfera e suolo, inteso come mare o come terra. Le
interazioni, gli scambi, tra suolo ed atmosfera sono intesi in termini di scambi di
masse d’acqua (evaporazione, condensazione e precipitazioni), e di energia (calore
sensibile, calore latente e radiazione).
Per come è stato definito lo Strato Limite Atmosferico, risulta piuttosto difficile
delimitarne un confine netto col resto dell’atmosfera e quindi definirne in maniera
precisa il suo spessore. Dove per spessore dello SLA s’intende quella quota alla
quale il terreno non influenza più l’evoluzione delle masse d’aria.
Lo spessore dello Strato Limite Atmosferico in una zona dipende infatti dalla
particolare condizione meteorologica, per cui, una volta assegnata la località, non è
noto lo spessore dello SLA.
Lo spessore dello SLA è, per esempio, fortemente legato al concetto di stabilità
atmosferica, concetto che sarà chiarito in seguito. In notti chiare e poco ventilate,
condizione di stabilità termica, lo spessore dello strato limite è di 100 m circa; in una

13. 3
giornata estiva molto soleggiata, condizione di instabilità, lo SLA può estendersi
fino a 2 km.
Lo spessore dello SLA è inoltre legato alla rugosità del terreno ed alla sua
complessità, dove per complessità di un terreno intendiamo una sua caratteristica
legata alla distribuzione sul territorio di colline e montagne ed alla pendenza dei loro
versanti. Sul mare lo spessore dello SLA è minore che in terra ferma dove aumenta
ulteriormente quando l’orografia diventa particolarmente complessa.
Per quanto riguarda l’ambito della tesi, è lecito considerare lo SLA esteso fino a
1000 m di quota dove i rilievi sono alti al massimo 200m. In tutte le simulazioni del
presente lavoro si farà riferimento a condizioni di stabilità neutra dell’atmosfera, con
altezza dello SLA dipendente in genere dalla complessità dell’orografia ovvero dalla
dimensione dei rilievi del terreno in studio.
Canopy
layer
Figura 1-1 – Strato Limite Atmosferico (SLA).
In figura 1-1 è rappresentato un tipico profilo di velocità del vento, wind shear, in
esso si riconoscono diversi sottostrati. Il sottostrato più vicino al terreno è chiamato
“Strato delle asperità” (Canopy Layer), il quale si estende al di sotto dell’altezza
media delle asperità, quali edifici, alberi ecc.. Il flusso principale nel Canopy Layer è
fortemente disturbato dalle singole asperità e risulta quindi disordinato e molto poco
omogeneo, rendendo difficile il suo studio che viene sovente trascurato
Al di sopra delle asperità si estende lo Strato Limite Superficiale (SLS), che
occupa il 10% circa dello SLA. All’interno dello SLS non si osserva una deviazione
del vento medio provocato dalla forza deviante (forza di Coriolis). L’altezza dello

14. 4
strato superficiale è tipicamente di 50m ma può variare in un intervallo compreso tra
5m e 200m in relazione all’altezza dello SLA.
L’ultimo sottostrato dello SLP è lo strato di Ekman o strato esterno (Outer Layer).
Nello strato di Ekman si verifica una rotazione del vento dalla direzione che esso
possiede al suolo fino alla direzione del vento indisturbato, alla cosiddetta altezza di
gradiente (Gradient Height) che è generalmente dell’ordine di 2000m.
Quando le isobare sono tra loro parallele, al di fuori dello SLA si instaura il vento
geostrofico che è, esso stesso, parallelo alle isobare. Il vento geostrofico è una
condizione ideale ma utile ai fini del presente lavoro.
Molti studi teorici e sperimentali sullo SLA escludono dalle loro
considerazioni la parte più bassa dello SLA, lo strato delle asperità (canopy layer) o
strato rugoso, inoltre, visti gli obbiettivi di questo lavoro, rivolti alla possibilità di
sfruttamento dell’energia eolica, è utile concentrare l’attenzione sui i primi 200m di
altitudine, all’interno dello Strato Superficiale, dove si possono trascurare gli effetti
della forza di Coriolis.
1.3 Statica dell’atmosfera.
Prima di descrivere alcune caratteristiche della dinamica dell’atmosfera utili allo
studio dello SLA, si vogliono fare dei brevi richiami di termodinamica e statica
dell’atmosfera.
1.3.1 L’aria umida atmosferica.
Senza entrare nel merito della composizione chimica, l’aria umida atmosferica si
può considerare costituita da una miscela bifasica di aria secca e vapore acqueo.
L’equazione di stato dei gas ideali per l’aria secca è data da:
TRmVp asasas ⋅⋅=⋅ (1.1)
Per il vapore acqueo invece si ha:
TRmVp VVV ⋅⋅=⋅ (1.2)
Per la miscela “aria umida” si ha invece l’equazione
TRmVp ⋅⋅=⋅ (1.3)
Passando attraverso la definizione di umidità specifica q si può definire una nuova
temperatura detta temperatura virtuale Tv.
m
m
q V
= umidità specifica (frazione massica) (1.4)
TqRmVp as ⋅⋅+⋅⋅=⋅ )61,01( (1.5)

15. 5
TqTV ⋅⋅+= )61,01( temperatura virtuale (1.6)
Con la temperatura virtuale si può scrivere l’equazione di stato dell’aria umida
continuando ad utilizzare nell’equazione di stato la costante specifica dell’aria secca.
Vas TRmVp ⋅⋅=⋅ (1.7)
1.3.2 Il gradiente verticale di temperatura e l’atmosfera politropica.
Si definisce gradiente verticale di temperatura Γ dalla relazione seguente:
z
T
∂
∂
=Γ gradiente verticale di temperatura (1.8)
All’interno dell’atmosfera la temperatura varia con la quota z in maniera variabile
con le condizioni attuali dei vari strati che la compongono. Se limitiamo l’attenzione
alla bassa atmosfera, cioè allo SLA, tra le atmosfere “convenzionali” quella che
approssima maggiormente la realtà è l’atmosfera politropica. Si ha un’atmosfera
politropica quando il gradiente verticale di temperatura è costante con la quota,
ovvero quando la temperatura T varia linearmente con la quota z.
02
2
=
∂
∂
=
∂
Γ∂
z
T
z
condizione di atmosfera politropica (1.9)
zTzT ⋅Γ+= 0)( profilo di temperatura per la (1.9) (1.10)
Applicando l’equazione fondamentale della statica dei fluidi, l’equazione di stato
(1.3), e considerando inoltre costante l’umidità specifica q, si ottengono i seguenti
profili di pressione e densità.
Γ⋅
−






⋅=
R
g
T
zT
pp
0
0
)(
profilo di pressione per la (1.9) (1.11)
Γ⋅
Γ⋅+
−






⋅=
R
Rg
T
zT
0
0
)(
ρρ profilo di densità per la (1.9) (1.12)
1.3.3 La stabilità atmosferica.
Il concetto di stabilità atmosferica è legato al gradiente verticale di temperatura.
Supponiamo di seguire una bolla d’aria che sale nell’atmosfera a velocità costante w,
considerando che la bolla, nel suo moto ascendente, non scambi né calore né lavoro
con l’ambiente circostante, questa si raffredda seguendo una trasformazione
adiabatica.

16. 6
Così, a seconda del gradiente verticale di temperatura dell’atmosfera, la bolla, che
viaggia verticalmente, si può trovare immersa in un ambiente a temperatura
maggiore, uguale o inferiore.
Se la bolla si trova immersa in una massa d’aria a temperatura inferiore essa
continuerà a salire e la condizione si dice instabile; se la bolla si trova immersa in
una massa d’aria a temperatura maggiore il suo moto ascensionale viene ostacolato e
l’atmosfera è stabile. Se il gradiente reale è pari alla variazione di temperatura della
bolla per metro percorso la condizione e di stabilità neutra.
In condizione di stabilità neutra l’atmosfera si dice adiabatica e, in effetti solo in
questo caso, sono inibiti gli scambi di calore tra bolla d’aria e ambiente circostante.
Il concetto stesso di “bolla d’aria” è un’astrazione dato che si sono ignorati i
processi di rimescolamento delle masse d’aria “bolla” e “atmosfera circostante”.
Quando si definisce la stabilità dell’atmosfera si mette a confronto quindi il
gradiente reale di temperatura col gradiente adiabatico. Il gradiente adiabatico può
essere ricavato partendo dall’equazione dell’energia:
=0 dh0
dzgdwdh ⋅++= 2
2
1
0
Considerando la velocità ascensionale w costante
dzgdh ⋅+=0
dzgdTcp ⋅+=0
Da cui si ottiene il gradiente adiabatico per l’aria secca, pari a:
mCmC
c
g
dz
dT
pad
ad 100/1/009.0
5.1004
066.9
°≅°=−=−==Γ (1.13)
Come gradiente adiabatico secco si considera, in genere, una diminuzione di 1°C
ogni 100 m di quota.
Il gradiente reale di temperatura varia con la quota ed è dato dalla derivata prima
di T rispetto alla quota z, equazione (1.15):
T=T(z) profilo di temperatura (1.14)
z
zT
z
∂
∂
=Γ
)(
)( gradiente verticale di temperatura (1.15)
A causa dell’umidità dell’aria, il concetto di stabilità atmosferica si complica.
Quando l’aria non è satura si può considerare ancora il gradiente adiabatico secco,
ma quando l’aria raggiunge la condizione di saturazione occorre considerare il
gradiente adiabatico saturo, pari a 0,65 °C/100m. Il gradiente adiabatico saturo tiene

17. 7
conto della cessione, sia di calore sensibile sia di calore latente da parte del vapore
che condensa.
Da quanto detto precedentemente si possono individuare tre condizioni di
stabilità, a cui corrispondono tre diversi tipi di atmosfera:
Tabella 1-1 – Classificazione delle condizioni atmosferiche secondo le condizioni di stabilità.
Per essere più precisi nel determinare la condizione di stabilità si utilizza una
classificazione introdotta nel 1961 da Pasquill e Gilford, secondo la qulae si passa da
condizioni di instabilità (classi A, B e C) alla classe di stabilità neutra (D), fino alle
condizioni di stabilità (classi E, F e G). Le classi di stabilità Pasquill si differenziano
secondo il gradiente di temperatura come riportato in tabella 1-2.
Classe Pasquill
Grado di stabilità
dell’atmosfera
Gradiente termico
dell’atmosfera
(°C/100 m)
A Instabilità forte <-1,9
B Instabilità moderata -1,9÷-1,7
C Instabilità debole -1,7÷-1,5
D Neutralità -1,5÷-0,5
E Stabilità debole -0,5÷1,5
F Stabilità moderata 1,5÷4,0
G Stabilità forte >4,0
Tabella 1-2 – Classificazione della stabilità atmosferica, secondo il gradiente di temperatura (Finzi e
Brusasca, 1991), fonte [1].
La stabilità dell’atmosfera può essere determinata anche attraverso un gruppo
adimensionale detto numero di Richardson:
Numero di Richardson:
2






∂
∂
∂
∂
=
z
u
zg
Ri
θ
θ
(1.16)
Stabilità Γ > Γad atmosfera super-adiabatica
Stabilità neutra Γ = Γad atmosfera adiabatica
Instabilità Γ < Γad atmosfera sub-adiabatica

18. 8
Dove θ è la temperatura potenziale, definita come la temperatura acquistata da
una massa d’aria in seguito ad una trasformazione adiabatica che la porti alla
pressione di riferimento pR di 1000 mbar.
pc
R
Rp
p
T
−






⋅=θ temperatura potenziale (1.17)
In condizione di saturazione si sostituisce nell’espressione (1.16) del numero di
Richardson la temperatura potenziale virtuale θv al posto della temperatura
potenziale θ:
Numero di Richardson per aria satura:
2






∂
∂
∂
∂
=
z
u
zg
Ri
V
V
θ
θ
. (1.18)
In condizione di saturazione si usa la temperatura potenziale virtuale:
pc
R
R
VV
p
p
T
−






⋅=θ temperatura potenziale virtuale (1.19)
In condizione di non saturazione:
0<
∂
∂
z
θ
Ri<0 Instabilità
0=
∂
∂
z
θ
Ri=0 Stabilità neutra
0>
∂
∂
z
θ
Ri>0 Stabilità
In condizione di saturazione:
0<
∂
∂
z
Vθ
Ri<0 Instabilità
0=
∂
∂
z
Vθ
Ri=0 Stabilità neutra
0>
∂
∂
z
Vθ
Ri>0 Stabilità

19. 9
Esiste anche una terza grandezza che serve a descrivere la stabilità atmosferica.
Questa grandezza è la lunghezza di Monin-Obukhov, L, detta anche lunghezza di
stabilità. Essa si può ricavare dall’equazione dell’energia cinetica turbolenta TKE
(Turbulent Kinetic Energy). Secondo la definizione data in [5] la lunghezza di
Monin-Obukhov L è data da:
0
3
0
*
H
uc
g
T
L
p ⋅
⋅
=
κ
(1.20)
Dove T0 è la temperatura, H0 è invece definito dalla (1.21), il pedice 0 indica che
le grandezze sono valutate al suolo.
( )00 '' Vp wcH θ⋅⋅= . (1.21)
Dove ρΗ0 è il flusso di potenza termica, per unità d’area, in un flusso turbolento il
flusso di calore avviene principalmente a causa del miscelamento turbolento.
Nella teoria di similitudine proposta da Monin e Obukhov viene utilizzato il
gruppo adimensionale ζ, ovvero la quota z adimensionalizzata con la lunghezza di
Monin-Obukhov L.
L
z
=ζ
La lunghezza di Monin-Obukhov è definita anche come l’altezza z=L alla quale il
numero di Richardson assume valore unitario quando il terreno è riscaldato (H0
positivo), cioè quando il calore fluisce dal terreno all’atmosfera:
V
V
w
u
g
L
''
*2
θκ
θ
⋅
⋅
−= (1.22)
1.4 Lo strato limite turbolento, flusso su pareti lisce.
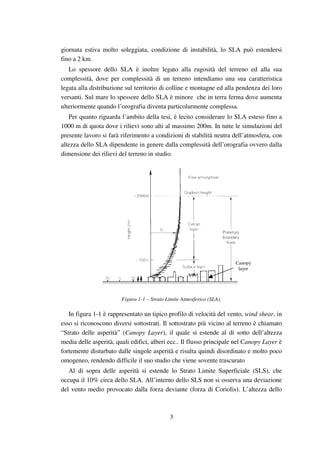
Come si vede dalla figura 1-2, si suole suddividere lo strato limite turbolento in
almeno tre regioni principali:
1. sottostrato viscoso – dove prevale l’effetto dell’attrito viscoso (flusso
laminare)
2. strato di sovrapposizione – nel quale gli effetti delle τ laminari e turbolente
sono di pari importanza
3. strato esterno – il flusso è turbolento, dominano gli effetti delle azioni
tangenziali turbolente

20. 10
Figura 1-2 – Profilo di strato limite turbolento su parete liscia.
1.4.1 Sottostrato Viscoso.
La velocità u dipende dalla τ di parete τw, dalla distanza dalla parete y, e dalle
proprietà del fluido ρ e µ ma è indipendente dallo spessore dello strato (Prandtl
1930)
),,,( µρτφ wyu =
Applicando l’analisi dimensionale si ricava l’espressione:








=
υ
ρτ
ρτ
w
w
y
f
u
Introducendo le coordinate di Von Karman u+
, y+
così definite:
τu
u
u =+
e
υ
τ yu
y =+
dove l’espressione ρτ w è definita come velocità d’attrito uτ si ottiene
( )++
=




 ⋅
== yf
uy
f
u
u
u
υ
τ
τ
.
Il sotto strato viscoso è molto sottile ed al suo interno le azioni tangenziali τ si
possono considerare costanti e uguali a quelle di parete τw, per cui:
=≈
∂
∂
= w
y
u
τµτ costante

21. 11
Integrando da y=0 ad un generico y, applicando la condizione di non-
scivolamento per y=0 (u=0) e la definizione di velocità di attrito si può scrivere
un’espressione del profilo di velocità, valido nel sottostrato laminare, espresso
secondo le coordinate di Von Karman.
++
=
⋅
== y
uy
u
u
u
υ
τ
τ
(1.24)
1.4.2 Strato esterno.
All’interno dell’intervallo indicato in figura 1-2 come fully turbulent region o log-
law region il profilo di velocità può essere espresso mediante una legge logaritmica
(log-law), che, per pareti lisce, è data dall’equazione.
( ) By
u
u
u +== ++
ln
1
κτ
(1.25)
I valori delle costanti κ e B sono stati ricavati sperimentalmente e si trovano in
letteratura. Generalmente, per κ, la costante di Von Karman, si assume un valore pari
a 0,42, mentre per B, si ha un valore di 5,45.
L’equazione (1.25), che rappresenta la legge logaritmica per pareti lisce, può
essere scritta anche in diversa forma:
( )++
⋅= yEu ln
1
κ
(1.26)
La costante E della (1.26) è tale che )ln(
1
EB
κ
= ovvero:
86,9)42,045,5exp()exp( =⋅=⋅= κBE
In letteratura si possono trovare valori leggermente diversi delle costanti E, B e
κ. Lo SLA è praticamente sempre di tipo turbolento, per lo meno quando il vento è
sufficientemente elevato da potersi sfruttare per fini energetici, ma, come si vedrà in
avanti, per lo SLA si utilizzano leggi modificate, che tengono conto della rugosità del
terreno, della stabilità atmosferica e della forza di Coriolis.

22. 12
1.5 Effetto della rugosità delle pareti sullo strato limite
turbolento.
La rugosità del terreno, o di qualsiasi altra parete, ha, sullo strato limite
turbolento, un’influenza in termini di forma del profilo di velocità. Quando la
rugosità delle pareti non influisce sul profilo di velocità si instaura un regime che si
definisce idrodinamicamente liscio; quando la rugosità è sufficientemente elevata si
instaura un regime detto idrodinamicamente rugoso. In figura 1-3 sono rappresentati
sul piano semilogaritmico (u+
,y+
) due profili di strato limite turbolento, uno per il
regime idrodinamicamente liscio, analogo alla figura 1-2, e l’altro per regime un
regime idrodinamicamente rugoso.
Lo strato limite atmosferico è notevolmente influenzato dalla rugosità del terreno.
Infatti superfici lisce come il mare od i terreni innevati presentano piccole resistenze
al flusso, mentre superfici con notevoli asperità, come le città o le foreste, offrono
una elevata resistenza. Il profilo di velocità del vento relativo ad un certo terreno è
espresso generalmente con delle leggi di tipo logaritmico oppure di tipo potenziale.
0.1 1 10 100 1 .10
30
5
10
15
20
25
regime idrodinamicamente liscio
regime idrodinamicamente rugoso
y+
u+
8 30
Figura 1-3 – Profili di velocità nel caso di flussi su pareti in regime idrodinamicamente liscio e
rugoso.
La legge logaritmica che descrive il profilo di velocità, nel caso di pareti non
lisce, si esprime secondo l’equazione (1.27).
( ) ByEu ∆−⋅= ++
ln
1
κ
(1.27)

23. 13
L’equazione precedente comprende la legge valida per pareti lisce (1.26), quando
il termine ∆B a secondo membro si annulla. Il termine ∆B prende il nome di
Funzione di Rugosità (Roughness Function), ed ha l’effetto di traslare il profilo
logaritmico per pareti lisce sul piano semi-logaritmico u+
ln(y+
), come si vede dalla
figura 1-3.
La Funzione di Rugosità ∆B si può trovare in letteratura espressa anche come
∆U/uτ, dove, se con ∆U s’intende il rallentamento rispetto al flusso su pareti lisce ∆B
risulta il rallentamento ∆U adimensionalizzato con la velocità d’attrito uτ.
Un’altra maniera per esprimere il profilo di velocità del vento è dato dalla
seguente equazione.






=+
0
ln
1
z
z
u
κ
legge logaritmica (log-law) (1.28)
Il parametro z0 che compare nell’equazione (1.28) prende il nome di Lunghezza di
Rugosità (Roughness Length). La lunghezza di rugosità z0 è legata alla rugosità del
terreno, ed è legata alla Funzione di Rugosità ∆B. Dal confronto dell’equazione
(1.27) con la (1.28) si ottiene una relazione tra la lunghezza di rugosità z0 e la
funzione di rugosità ∆B.
Infatti:
( ) ByE
z
z
∆−⋅=




 +
ln
1
ln
1
0 κκ
B
uz
E
z
z
∆−




 ⋅⋅
⋅=





µ
ρ
κκ
τ
ln
1
ln
1
0





 ⋅⋅
⋅=∆
µ
ρ
κ
τuz
EB 0
ln
1
, ed infine
( )Re*ln
1
⋅=∆ EB
κ
(1.29)
Il gruppo adimensionale Re* che compare nell’espressione (1.29) è detto numero
di Reynolds di rugosità (roughness Reynolds number). Si noti che Re* assume un
valore minimo nel caso di flusso su pareti lisce (∆B=0).
( ) 0Re*ln
1
=⋅E
κ
1*Re =⋅E
( ) 102,0
81,9
11
Re* min =≈=
E

24. 14
In letteratura si possono trovare dei valori leggermente diversi del minimo valore
di Re*, secondo il valore assunto per E.
Per quanto riguarda lo strato limite atmosferico, la rugosità del terreno è definibile
in diversi modi. Si potrebbe pensare ad esempio, alla stessa definizione data per le
tubazioni come l’altezza media h delle asperità che sporgono dalla superficie.
Intuitivamente si può pensare che lo Strato Limite Atmosferico sia influenzato non
solo dall’altezza media degli ostacoli h, ma anche dalla loro distribuzione sul
territorio e dalla superficie frontale S che, mediamente, ogni ostacolo espone al
vento.
Si può definire un’altezza delle asperità adimensionalizzata h+
in maniera analoga
a Re*.
µ
ρ hu
h
⋅⋅
=+ *
(1.30)
È da notare che, per come sono definiti i gruppi adimensionali h+
e Re*, vale
l’eguaglianza:
+
=
hh
z Re*0
(1.31)
In letteratura, vedi [5] e [9], si trovano diverse formule empiriche che danno un
legame tra l’altezza media delle asperità h e lunghezza di rugosità z0. Ad esempio la
seguente relazione dovuta a Nikuradse [9]
30
0
h
z = (1.32)
La relazione proposta da Nikuradse è stata ottenuta per flusso all’interno di
tubazioni con le pareti ricoperte da uno strato uniforme di sabbia. Il valore di h in
questo caso è da considerarsi pari al diametro medio dei granelli di sabbia.
Il caso studiato da Nikuradse si adatta male alla propagazione dello Strato Limite
Atmosferico, altre formule empiriche, ricavate da esperimenti in galleria del vento o
da studi diretti sullo SLA, sono utilizzate per ottenere il rapporto z0/h.
Detta Ah la superficie di suolo mediamente occupata da un ostacolo, ed S la
superficie dell’ostacolo esposta frontalmente al vento, Lettau [5] propose nel 1969 la
seguente formula:
hA
Sh
z
⋅
⋅= 5.00 (1.33)
Da risultati sperimentali ottenuti in galleria del vento e riportati in [9], il rapporto
z0/h si assesta a valori di 1/15 per valori di Re*>1 o di h+
>20.
per Re*>1 o (h+
>20):

25. 15
15
0
h
z ≈ Snyder e Castro [9]. (1.34)
La lunghezza di rugosità z0 è riportata in letteratura per diversi tipi di superfici ed
alcuni valori, relativi a vari tipi di terreno sono rappresentati in tabella 1-3 e in figura
1-4 con i corrispondenti profili del vento.
Tipologia del terreno z0 [m]
Terreni fangosi,paludi, ghiacci Da 10-5
a 3 10-5
Mare calmo Da 2 10-4
a 3 10-5
Sabbia Da 2 10-4
a 10-3
Pascoli erbosi Da 0,001 a 0,01
Erba bassa Da 0,01 a 0,04
Campo incolto Da 0,02 a 0,03
Erba alta Da 0,04 a 0,1
Foreste e boschi Da 0,1 a 1
Abitato tipo sobborgo Da 1 a 2
Città Da 1 a 4
Tabella 1-3 – Lunghezze di rugosità z0, fonte [5].
Figura 1-4 – Profili del vento corrispondenti a quattro diverse lunghezze di rugosità. Si vede come
dipenda dalla rugosità del terreno sia l’intensità del vento al suolo che l’altezza dello SLA.

26. 16
Le relazioni (1.31) e (1.32), proposte da Nikuradse e Lettau, non tengono conto di
Re*. Gli studi sperimentali di Snyder e Castro, ma anche le equazioni implementate
nel codice di calcolo utilizzato in questo lavoro tengono conto di come il rapporto
z0/h si modifichi al variare di Re* e h+
, ovvero secondo i diversi regimi idrodinamici.
La relazione di Lettau è specifica per strato limite atmosferico e tiene conto di uno
strato limite turbolento in regime idrodinamicamente rugoso. La formula di
Nikuradse è stata verificata sperimentalmente in galleria del vento da [9] solo per
valori di Re* e h+
molto piccoli. Quindi la formula di Lettau è da ritenersi più adatta
allo strato limite atmosferico rispetto alla formula di Nikuradse.
1.6 Effetto della stabilità atmosferica sul profilo di
velocità del vento.
Alcune delle relazioni che esprimono il profilo di velocità del vento, che tengono
conto della stabilità dell’aria, utilizzano il parametro adimensionale ζ=z/L.
( )





−





⋅= ζψ
κ 0
ln
1
* z
z
u
u
(1.35)
Nell’equazione (1.35) ψ=0 in condizioni di stabilità neutra si ricade nella legge
logaritmica (1.28). La funzione ψ(ζ) che compare in (1.35) viene espressa in diversa
maniera nei vari lavori scientifici, Jensen et al.(1984) proposero per essa la seguente
equazione (1.36), che poi è quella implementata nel codice WAsP:
( )



⋅−
−⋅−
=
ζ
ζ
ζψ
7.4
1161
)(
4/1
fonte [5]. (1.36)
La prima relazione in (1.36) è valida in condizioni di instabilità, la seconda in
condizioni di stabilità, per atmosfera adiabatica ψ=0 e si ricade nella (1.28).
Oltre a far riferimento ai profili del vento con andamento logaritmico si possono
considerare dei profili con legge di potenza. L’EPA (Environmental Protection
Agency) suggerisce, per quanto riguarda la dispersione degli inquinanti, l’uso di leggi
di potenza che tengono conto anche della classe di stabilità dell’aria oltre che della
rugosità del terreno.
p
z
z
u
u






=
1
2
1
2
fonte [1] (1.37)
dove con i pedici 1 e 2 si indicano due generiche quote z1 e z2 e con p un
parametro che varia da 0,09 per classe di stabilità A e suolo liscio, fino a 0,4 per
suolo rugoso e classi di stabilità F-G.
I valori del parametro p della (1.37) sono mostrati nella seguente tabella 1-4.

27. 17
Classe Pasquill Suolo rugoso Suolo liscio
A 0,15 0,09
B 0,15 0,09
C 0,20 0,12
D 0,25 0,15
E 0,40 0,24
F-G 0,40 0,24
Tabella 1-4 – Coefficienti p dell’equazione (1.37).
Utilizzando i coefficienti di tabella 1-4 si possono elaborare dei profili del vento
come quelli riportati in figura 1-5.
0 500 1000 1500 2000
0
10
20
30
40
50
classi A e B, suolo rugoso
classe C, suolo rugoso
classe D, suolo rugoso
classi E, F e G, suolo rugoso
classi A e B, suolo liscio
classe C, suolo liscio
classe D, suolo liscio
classi E, F e G, suolo liscio
quota z [m]
velocitàu[m/s]
Figura 1-5 – Profili di velocità del vento calcolati tramite la formula (1.37) per una velocità a 10 m
dal suolo di 5 m/s. I coefficienti p utilizzati sono quelli riportati in tabella 1-4.

28. 18
1.7 La legge logaritmica modificata.
La legge logaritmica (1.28) può essere modificata per tenere conto degli effetti
della forza di Coriolis. Si ottiene così la legge logaritmica modificata (modified log
law) [2], equazione (1.38), che si può ritenere valida fino a una quota di 300m in
condizioni di stabilità neutra.






⋅+





⋅=
h
z
z
zu
zU 75,5ln
*
)(
0κ
(1.38)
Con h, altezza di gradiente, che può essere stimata con la relazione seguente [2]:
f
u
h
⋅
≈
6
*
altezza di gradiente (1.39)
)sin(2 ϕ⋅Ω⋅=f parametro di Coriolis (1.40)
Un’altra legge logaritmica modificata è quella data da [14]:






⋅+




 +
⋅=
h
z
z
zzu
zU 75,5ln
*
)(
0
0
κ
(1.41)
1.8 Il vento alla Ekman.
Ekman trovò una soluzione analitica alle equazioni del moto all’interno dello SLA
sotto particolari ipotesi semplificative. Tra le varie ipotesi sotto le quali valgono le
relazioni proposte da Ekman c’è quella che KM, la viscosità cinematica effettiva, sia
costante. In questa maniera Ekman poté trattare analiticamente lo SLA in maniera
analoga ad uno strato limite laminare e mettere in evidenza la rotazione della
direzione del vento al variare della quota da quella che esso assume al suolo,
inclinata rispetto alle isobare, fino alla direzione del vento geostrofico, parallela alle
isobare.
Nelle equazioni seguenti sono riprodotti i valori delle componenti medie della
velocità U e V secondo la spirale di Ekman.
( ) ( )[ ]zazaVzU g ⋅⋅⋅−−⋅= 00 cosexp1)( (1.42)
( ) ( )zazaVfzV g ⋅⋅⋅−⋅⋅= 00 sinexpsgn)( (1.43)
Dove a0 è dato dalla relazione seguente:
MK
f
a
⋅
=
2
2
0 (1.44)
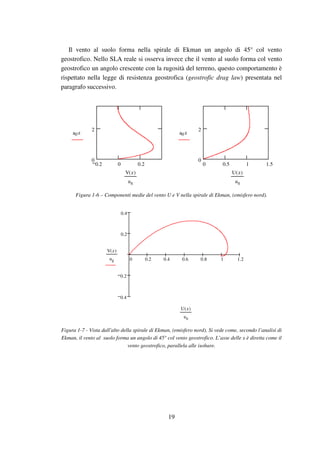
In figura 1-6 sono rappresentate le componenti U(z) e V(z) date rispettivamente
dalla (1.42) e (1.43); in figura 1-7 è tracciata la spirale di Ekman vista dall’alto.

29. 19
Il vento al suolo forma nella spirale di Ekman un angolo di 45° col vento
geostrofico. Nello SLA reale si osserva invece che il vento al suolo forma col vento
geostrofico un angolo crescente con la rugosità del terreno, questo comportamento è
rispettato nella legge di resistenza geostrofica (geostrofic drag law) presentata nel
paragrafo successivo.
0.2 0 0.2
0
2
a0 z⋅
V z( )
ug
0 0.5 1 1.5
0
2
a0 z⋅
U z( )
ug
Figura 1-6 – Componenti medie del vento U e V nella spirale di Ekman, (emisfero nord).
0 0.2 0.4 0.6 0.8 1 1.2
0.4
0.2
0.2
0.4
V z( )
ug
U z( )
ug
Figura 1-7 - Vista dall'alto della spirale di Ekman, (emisfero nord). Si vede come, secondo l’analisi di
Ekman, il vento al suolo forma un angolo di 45° col vento geostrofico. L’asse delle x è diretta come il
vento geostrofico, parallela alle isobare.

30. 20
1.9 Legge di resistenza geostrofica ed il vento
geostrofico.
Sussiste un equilibrio tra forza d’attrito al suolo e la forza esercitata dal gradiente
orizzontale di pressione. In condizioni di neutralità atmosferica il suddetto equilibrio
è stato studiato da Rossby e Montgomery (1935). Il risultato di questo equilibrio è la
legge di resistenza geostrofica (geostrofic drag law), [5]:
2
2
0
*
ln
*
BA
zf
uu
Vg +







−





⋅
=
κ
(1.45)
gV
uB
⋅
⋅
−=
κ
α
*
sin (1.46)
La legge di resistenza geostrofica è stata ricavata in condizioni di neutralità
atmosferica. Le costanti empiriche A e B di (1.45) e (1.46) valgono rispettivamente 2
e 4,5 circa. L’angolo α della (1.46) è l’angolo che il vento al suolo forma col vento
geostrofico. Si è osservato come il vento al suolo generalmente ha un’intensità di
circa la metà di quella del vento geostrofico, e forma con esso un angolo α di 30°
circa sopra terreni molto rugosi, inclinato verso le basse pressioni. Su superfici lisce
come il mare il vento al suolo si può considerare circa due terzi del vento geostrofico
ed è inclinato rispetto ad esso di 10°÷15° verso le basse pressioni.
In figura 1-8 è rappresentata una vista dall’alto del vento al variare della quota z.
In figura 1-8 gli assi sono adimensionalizzati mediante le formule (1.47) e (1.48),
anche la quota z è adimensionalizzata in un gruppo che comprende il parametro di
Coriolis e la velocità d’attrito.
( ) */ uuUF gx −= (1.47)
( ) */ uvVF gy −= (1.48)

31. 21
Figura 1-8 – Rappresentazione del vento al variare della quota z. Fx e Fy definiti come (1.47) e (1.48),
fonte [12].
È possibile estendere la legge di resistenza geostrofica a condizioni di non
neutralità. Per atmosfera non neutra A e B sono funzioni del parametro di stabilità µ,
dipendente a sua volta dalla lunghezza di Monin-Obukhov L.
Lf
u
⋅
⋅
=
*κ
µ (1.49)

32. Capitolo 2 Impostazioni per le simulazioni.
2.1 Le equazioni generali del moto.
Per studiare il flusso dei fluidi si fa ricorso alle equazioni di conservazione della
massa, della quantità di moto e dell’energia, in forma differenziale. Esse possono
essere scritte nella forma conservativa o non conservativa; di seguito sono riportate
le equazioni non conservative in forma vettoriale:
Equazione di continuità, conservazione della massa:
0=•∇⋅+ V
dt
d
ρ
ρ
(2.1)
Equazione della quantità di moto, conservazione della quantità di moto:
( ) Fp
xdt
Vd
ij
j
⋅+∇−
∂
∂
= ρτρ (2.2)
Equazione dell’energia, conservazione dell’energia:
E
j
iji
ST
x
u
V
dt
de
+∇⋅•∇+
∂
⋅∂
+⋅•−∇= ))((
)(
)( λ
τ
ρρ (2.3)
Dove per e s’intende l’energia specifica somma di energia interna ed energia
cinetica dell’unità di massa.
Secondo l’Ipotesi di Stokes (1845), gli sforzi tangenziali possono essere espressi
in funzione dei gradienti di velocità (ipotesi di fluido newtoniano);
V
x
u
x
u
ij
i
j
j
i
ij •∇⋅





−⋅+








∂
∂
+
∂
∂
= µδµτ
3
2
(2.4)
sostituendo nel sistema l’espressione di τij, le incognite del sistema sono u, v, w,
ρ, p, T, µ, e e λ, per un totale di nove, funzioni di x, y, z e t. Le cinque equazioni
scalari di conservazione costituiscono, insieme alle seguenti quattro relazioni di
stato, un sistema chiuso di equazioni differenziali alle derivate parziali.

33. 23
Caratteristiche fisiche dipendenti dallo stato termodinamico (p,T):
densità ),( Tpρρ =
entalpia ),( Tphh =
viscosità ),( Tpµµ =
conducibilità termica ),( Tpλλ = .
Una delle varie soluzioni delle equazioni del moto, particolarmente interessante
per il lavoro presente, è il vento secondo Ekman. Ekman studio il vento all’interno
dello strato limite atmosferico, e, sotto determinate ipotesi semplificative tra cui
quelle di considerare la densità dell’aria e la viscosità turbolenta costanti in tutto lo
strato d’attrito, calcolò un andamento del vento detto a spirale di Ekman. La
deviazione del vento con la quota, cioè la spirale di Ekman, è dovuta all’effetto della
forza di Coriolis.
2.2 La turbolenza. Modello di turbolenza utilizzato.
Nello strato limite atmosferico si instaura quasi sempre un regime turbolento;
conseguentemente i flussi studiati nel presente lavoro sono tutti turbolenti e
stazionari. In realtà, con la dicitura di flussi turbolenti stazionari si intendono
indicare dei flussi turbolenti, stazionari in media, ovvero ergodici. Per studiare la
turbolenza occorre, in qualche modo, modificare le equazioni del moto e, a tal fine,
esistono diversi approcci, ciascuno dei quali è caratterizzato dalla scala minima di
risoluzione della turbolenza. In generale i metodi usati sono tre:
• Le equazioni mediate secondo Reynolds, (Reynolds Averaged N-S , RANS
Equations)
• Large Eddy Simulation, LES
• Simulazione Numerica Diretta (Direct Numerical Simulation, DNS)
Le equazioni RANS (Reynolds Averaged Navier Stokes) sono quelle che si
ottengono a partire dalle equazioni generali di Navier-Stokes (N-S) applicando alle
grandezze u, v e w la decomposizione di Reynolds e mediando nel tempo. Al sistema
originale di equazioni si sostituisce, dunque, un analogo sistema di equazioni
differenziali alle derivate parziali. Nel nuovo sistema di equazioni, al posto delle
incognite citate nel paragrafo precedente compaiono le stesse grandezze ma mediate

34. 24
nel tempo, e compaiono dei termini aggiuntivi, definiti sforzi di Reynolds,
ji uu '' ⋅⋅− ρ , che, nel caso tridimensionale, costituiscono altre 6 nuove incognite.
Per poter risolvere il sistema di equazioni di conservazione, nel caso di flussi
turbolenti occorre fare delle ipotesi sugli sforzi di Reynolds, ovvero scrivere delle
ulteriori equazioni che permettano di ottenere nuovamente un numero di equazioni
indipendenti pari al numero delle incognite.
L’ipotesi di Boussinesq prevede che per gli sforzi turbolenti si possa definire
un legame con i gradienti di velocità, analogo a quello relativo al moto
laminare.
V
x
U
x
U
uu ijt
i
j
j
i
tjitij •∇⋅⋅⋅−








∂
∂
+
∂
∂
=⋅−= δµµρτ
3
2
'')( (2.5)
La grandezza tµ , viscosità turbolenta, secondo la formula di Prandtl (2.6), è
proporzionale al prodotto tra densità e due grandezze di scala dei vortici, una
lunghezza ed una velocità:
SSt V⋅⋅∝ ρµ (2.6)
Dove:
S lunghezza di scala
VS velocità di scala
Si è soliti classificare i modelli di turbolenza secondo il numero di equazioni
differenziali che vengono aggiunte alle equazioni di conservazione per chiudere il
sistema. In particolare, nel modello k-ε le due grandezze di scala vengono definite
nella maniera seguente:
2/1
kS =
ε
2/3
k
VS =
dove
k, l’energia cinetica turbolenta è definita come:
( )222
'''
2
1
wvuk ++= (2.9)
ed ε è la velocità di dissipazione dell’energia cinetica turbolenta, dovuta alla
turbolenza di piccola scala, così come previsto dalla teoria della energy cascade, che
prevede il trasferimento dell’energia cinetica dal flusso medio ai vortici di

35. 25
dimensione maggiore e da questi ultimi, verso i vortici di scala inferiore, fino a quelli
caratterizzati da lunghezze di scala comprese nell’intervallo 0,01÷0,1mm.
Sostituendo nella formula di Prandtl (2.6) per la viscosità turbolenta si ottiene
ερ⋅=µ µ
2kCt , (2.7)
con Cµ coefficiente di proporzionalità, caratteristica del modello k-ε. Per gli Sforzi
di Reynolds si potrà scrivere:
k
x
U
x
U
uu ij
i
j
j
i
tjitij ⋅⋅⋅−








∂
∂
+
∂
∂
=⋅−= δρµρτ
3
2
'')( (2.8)
Il sistema di equazioni differenziali viene quindi chiuso con altre due equazioni
differenziali, che definiscono il modello matematico per le grandezze k e ε.
Il modello k-ε è pertanto un modello a due equazioni, di seguito descritte
Equazione dell’energia cinetica turbolenta, k (TKE):
ερ
σ
µ
µρ ⋅−++





∂
∂






+
∂
∂
=⋅ bk
ik
t
i
GG
x
k
xdt
dk
(2.10)
Dove il termine Gk è la produzione di energia cinetica turbolenta dovuta ai
gradienti di velocità media.
i
j
jik
x
u
uuG
∂
∂
⋅⋅−= ''ρ (2.11)
Gb è invece la produzione di energia cinetica turbolenta dovuta alla presenza di
forze di galleggiamento, definita da [3]:
it
t
ib
x
T
gG
∂
∂
⋅⋅⋅=
Pr
µ
β (2.12)
con β coefficiente di dilatazione termica [3]:
pT






∂
∂
−=
ρ
ρ
β
1
. (2.13)
Nel caso di gas ideali e supponendo le forze gravitazionali dirette secondo la
direzione –y si ottiene:
y
gG
t
t
b
∂
∂
⋅
=
ρ
ρ
µ
Pr
(2.14)
Nell’equazione dell’energia cinetica turbolenta compare ε, la velocità di
dissipazione di k. Per ε sussiste una ulteriore equazione che completa il modello.

36. 26
equazione della velocità di dissipazione della turbolenza, εεεε (TDR):
( )
k
CGCG
k
C
xxdt
d
bk
i
t
i
2
231
ε
ρ
εε
σ
µ
µ
ε
ρ
ε
−⋅++





∂
∂






+
∂
∂
=⋅ (2.15)
In questa maniera è possibile chiudere il set di equazioni differenziali. Cµ, C1, C2,
Prt, σk e σε sono delle costanti del modello, ed i loro valori variano secondo il caso in
studio, mentre il valore di C3 viene calcolato dal codice mediante un’ulteriore
equazione algebrica riportata in [3].
Generalmente per le costanti del modello k-ε si assumono dei valori tipici, che
compaiono come default in FLUENT, riportati in tabella 2-1.
Costanti del modello standard k-ε, valori di default in FLUENT
Cµ C1 C2 σκ σε Prt
0,09 1,44 1,92 1 1,3 0,85
Tabella2-1 – Valori di default in FLUENT delle costanti del modello k-ε.
2.3 Il metodo numerico di risoluzione delle equazioni del
moto. Discretizzazione del dominio di calcolo e delle
equazioni del modello.
Per risolvere numericamente le equazioni del moto in un dato dominio di
dimensioni finite, occorre innanzitutto procedere alla sua discretizzazione, ovvero
alla creazione, di una griglia di punti, detti nodi, e di un insieme di sottodomini sui
quali applicare le equazioni fondamentali.. La creazione del dominio di calcolo e la
sua discretizzazione, in tutte le simulazioni svolte, è stata effettuata mediante un
preprocessore, GAMBIT, sempre della Fluent Inc..
I domini studiati nelle simulazioni bidimensionali (tridimensionali) sono stati
suddivisi in griglie di tipo map, formate da sole celle quadrangolari (esaedriche) con
i nodi posti nei vertici delle celle..
Per quanto riguarda la discretizzazione delle equazioni del modello, il codice
utilizzato, Fluent, utilizza la tecnica dei volumi finiti.
Per capire cosa significhi discretizzare un’equazione differenziale osserviamo la
generica equazione di conservazione (2.16), valida in condizioni di stazionarietà e
per flussi bidimensionali [17].
( ) ( ) S
yyxx
V
y
U
x
+











∂
∂
Γ
∂
∂
+





∂
∂
Γ
∂
∂
=





∂
∂
+
∂
∂ φφ
φρφρ (2.16)

37. 27
Le grandezze φ, Γ e S che compaiono nella equazione precedente, rappresentano
delle variabili diverse a seconda della equazione di conservazione considerata. Nel
caso bidimensionale, con il modello di turbolenza k-ε, tali variabili sono riassunte
nella tabella 2-2 seguente:
Equazione φ Γ S
x-NS U µτ xp ∂∂− +Fx
y-NS V µτ yp ∂∂− +Fy
k k µτ/σκ Gk-ρε
ε ε µτ/σε (ε/k)(C1Gk-C2ρε)
continuità  0 0
Tabella 2-2 – Schema riassuntivo delle variabili della equazione generica di convezione-diffusione
(2.16).
Nell’equazione generale di conservazione (2.16), il termine a primo membro è il
termine convettivo e a secondo membro, tra parentesi quadre, il termine diffusivo,
dove Γ è un generico coefficiente di diffusività, dovuto alla somma di diffusività
molecolare e turbolenta. Col termine S si indica la somma algebrica di produzione e
distruzione della grandezza generica φ.
In seguito all’integrazione dell’equazione (2.16) su un volumetto di controllo
contenente il nodo P, tratteggiato nel dominio bidimensionale di figura 2-1, si ottiene
la (2.17).
( ) ( )[ ] ( ) ( )[ ]
yxSx
dy
d
dy
d
y
dx
d
dx
d
xVVyUU
snwe
snwe
∆⋅∆⋅+∆














Γ−





Γ+∆











Γ−





Γ=
=∆−+∆−
φφφφ
φρφρφρφρ
(2.17)
Nella (2.17) c’è la necessità di sostituire il valore della grandezza generica φ e
delle sue derivate parziali nei punti medi sulle facce della superficie di controllo,
contrassegnati con le lettere minuscole e, w, s, e n, mediante i valori delle variabili
nei punti nodali E, W, S e N.

38. 28
s
n
w e
V.C.
W E
S
P
N
∆y
∆x
Figura 2-1 – Volume di controllo (area in 2D) sul quale viene integrata l’equazione generica di
conservazione (2.16) per ottenere la (2.17).
La generica equazione (2.17) diventa quindi una relazione algebrica lineare in
cinque variabili.
baaaaa WWSSEENNPP =⋅+⋅+⋅+⋅+⋅ φφφφφ (2.18)
Per ogni grandezza φ, si hanno tante equazioni quanti sono i nodi, che possono
essere risolte dal codice di calcolo Fluent in due diverse modalità, segregated o
coupled.
Il metodo di risoluzione segregated prevede che le diverse equazioni vengano
risolte non contemporaneamente in ogni punto spaziale, secondo una sequenza che
prevede di aggiornare in successione le variabili fisiche. Tale metodo è
particolarmente indicato per flussi incomprimibili [3], mentre per flussi
comprimibili, cioè per alti numeri di Mach, è più efficace la modalità coupled, così
chiamata perché consiste nella risoluzione contemporanea, in ciascun punto del
dominio, delle diverse equazioni di conservazione.
Particolari tecniche di discretizzazione sono riservate ai gradienti di pressione che
compaiono nelle RANS, i quali vengono stimati a partire da ipotesi sull’andamento
della pressione. Nelle simulazioni svolte si è sempre utilizzata la discretizzazione per
la pressione PRESTO!, acronimo di “PREssure STaggering Option”, caratterizzata
dal concetto di grid staggering, ovvero dal fatto di assegnare a punti diversi da quelli
nodali i valori di alcune grandezze, in questo caso della pressione. Quando i gradienti
di pressione sono molto bassi si può utilizzare come schema di interpolazione per la
pressione quello di default in Fluent, denominato standard.
Invece, alcuni casi in cui è consigliato l’uso di uno schema di interpolazione
diverso dallo standard sono flussi con elevate forze di campo, in presenza di moti
vorticosi (swirling flows), convezioni naturali caratterizzate da un alto numero di
Rayleigh e strati limite su pareti curve. La tecnica PRESTO! è applicabile solamente

39. 29
in griglie con celle quadrangolari in 2D o esaedriche in 3D, ed è disponibile solo
quando viene utilizzata la tecnica di risoluzione “segregated”; l’uso della
discretizzazione PRESTO! è consigliato in [3] per risolvere flussi dove sono
importanti le forze di galleggiamento (Driven Buoyancy Flows). Un’alternativa alla
discretizzazione PRESTO! può essere quella di tipo “Second Order Upwind” o
“Body Force Weighted”.
Inoltre nei flussi incomprimibili è necessario utilizzare una relazione di
accoppiamento tra pressione e velocità (pressure-velocity coupling), che il codice
utilizza per far comparire la pressione nella equazione di continuità discretizzata. Il
tipo di accoppiamento pressione-velocità scelto è il SIMPLEC, una variante
dell’algoritmo di default in Fluent, il SIMPLE. SIMPLE è l’acronimo di “Semi-
Implicit Method for Pressure Linked Equations”, mentre la sua variante SIMPLEC
sta per SIMPLE-Consistent e, sostanzialmente, può portare a convergenza più
velocemente le soluzioni in quei casi in cui è proprio l’accoppiamento pressione-
velocità a causare una certa instabilità della soluzione numerica.
Per ulteriori approfondimenti si rimanda alla sezione 17.3 di [3] in cui viene
trattato il metodo di risoluzione segregated e le possibili tecniche di discretizzazione.
2.4 Definizione delle caratteristiche fisiche dei materiali,
fluidi e solidi, considerati nelle simulazioni.
Per le simulazioni svolte sono stati definiti nel codice di calcolo due materiali, uno
fluido, l’aria, ed uno solido, il terreno. Le caratteristiche fisiche di aria e terreno sono
riportate rispettivamente in Tabella 2-3 e 2-4. Un limite derivante proprio dalla scelta
del fluido è quello di considerare aria secca e non umida, mentre, un elemento critico
della simulazione, soprattutto quando sono presenti forze di massa quali la forza
peso, è la scelta della relazione che definisce la densità del fluido.
Nome: Aria
Tipo di materiale: Fluid
Densità [kg/m3
]: 0,0104 T[K] – 1,7591
Calore specifico cp [J/(kg K)]: 1004,5
Conduttività termica [W/(m K)]: 0,0252
Viscosità dinamica [Pa s] 1,7894 10-5
Tabella 2-3 – Caratteristiche fisiche dell’aria.

40. 30
Occorre, quindi, soffermarsi sulla procedura seguita per la scelta della relazione
che lega la densità alla temperatura. In effetti, la scelta più appropriata per la densità
sarebbe quella di utilizzare la legge dei gas ideali ma, purtroppo, alcuni tipi di
condizioni al contorno, quali la outflow, non sono compatibili con tale legge. Altre
condizioni al contorno permettono l’utilizzo della relazione dei gas ideali ma non
sono indicate per flussi esterni. Si è pertanto definita la densità dell’aria come sola
funzione della temperatura statica, ad esempio tramite una legge polinomiale.
Facendo l’ipotesi di atmosfera adiabatica, e considerando l’aria un gas ideale a cp
costante, le variabili temperatura, pressione e densità variano con la quota con le
seguenti leggi:
zTzT ad ⋅Γ+= 0)( ipotesi di atmosfera adiabatica (2.19)
R
cp
T
zT
pzp 





⋅=
0
0
)(
)( (2.20)
R
cv
T
zT
z 





⋅=
0
0
)(
)( ρρ (2.21)
La relazione (2.21) può essere interpolata linearmente, senza commettere un
sensibile errore, dal suolo (z=0) fino ad una quota arbitraria alla quale si è
considerato che il vento assuma le caratteristiche di vento geostrofico, permettendo
di scrivere la relazione che compare in tabella 2-3. I coefficienti della retta
interpolante variano con temperatura e densità al suolo (T0 e ρ0), e con la quota alla
quale si è fissato il vento geostrofico. L’espressione lineare di tabella 2-3 è stata
ottenuta con T0=288,15 K e ρ0=1,225 kg/m3
, e considerando a 1000m la quota alla
quale s’instaura il vento geostrofico.
Nome: Terreno
Tipo di materiale: Solid
Densità [kg/m3
]: 2700
Calore specifico cp [J/(kg K)]: 400
Conduttività termica [W/(m K)]: 100
Tabella 2-4 – Caratteristiche fisiche del terreno.

41. 31
ρ = 0,0104 T - 1,7591
R2
= 1
1,1000
1,1200
1,1400
1,1600
1,1800
1,2000
1,2200
1,2400
276 278 280 282 284 286 288 290
temperatura T [K]
densitàρρρρ[kg/m3
]
Figura 2-2 – Interpolazione lineare della relazione ρ=ρ(T) nel caso di atmosfera secca adiabatica, T0
288,15 K, ρ0 1,225 kg/m3
, interpolazione tra i valori compresi nell’intervallo 0m÷1000m di quota.
Nel lavoro di S. Forma, [2], si era presa in considerazione una diversa relazione
tra densità e temperatura, facendo riferimento all’Atmosfera Internazionale Standard
per vedere come densità e temperatura variano con la quota. L’Atmosfera
Internazionale Standard considera un’atmosfera reale in condizione di neutralità,
influenzata dall’umidità, e per questo considera un gradiente termico inferiore (in
valore assoluto) a quello adiabatico secco, e considerando un’umidità specifica q che
diminuisce con la quota, facendo variare così grandezze quali la massa molare ed i
calori specifici.
Le impostazioni utilizzate in [2] per descrivere le caratteristiche fisiche dell’aria
sono riportate nella tabella 2-5 e, come detto precedentemente, sono diverse da
quelle utilizzate nel presente lavoro, almeno per quanto concerne le grandezze
densità e viscosità.
Per quanto concerne la viscosità molecolare, dal momento che nello strato limite
atmosferico si ha un flusso turbolento, con valori della viscosità turbolenta
mediamente cinque ordini di grandezza superiore a µ, si può assumere per
quest’ultima un valore costante. Risulta invece importantissimo stimare con
accuratezza la viscosità turbolenta µt e, in modo particolare, definire la scelta del
modello di turbolenza e delle sue costanti

42. 32
Tabella 2-5 – Caratteristiche fisiche dell'aria, impostazioni come [2].
In figura 2-2 sono riportati i risultati numerici di due simulazioni del flusso
bidimensionale su un terreno piano, il primo ottenuto con le nuove impostazioni
dell’aria, come da tabella 2-3, l’altro ottenuto con le caratteristiche dell’aria secondo
[2]. Il dominio di calcolo ha dimensioni pari a 6 km in direzione orizzontale e 1000
m in altezza. E’ stato impostato in ingresso un determinato profilo di velocità e in
figura 2-2 è mostrato il confronto con quello in uscita dal dominio di calcolo, dopo 6
km. Le caratteristiche di geometria, griglia e parametri impostati per la simulazione
verranno descritte in seguito. Si può anticipare che è considerato un buon risultato
quello che permette di avere in uscita uno strato limite completamente sviluppato che
si mantiene inalterato rispetto a quello impostato all’ingresso.
Name: Air
Material type: Fluid
Fluid materials: Air
Properties:
Density [kg/m3
]: Piecewise-linear
Temperature [K]: Density [kg/m3
] :
1 275,2 1,0066
2 278,4 1,0582
3 281,7 1,1117
4 284,9 1,1673
5 288,15 1,2250
Cp: 1004,5 J/(kg K)
Thermal conductivity: 0,0252 W/(m K)
Viscosity: Piecewise-linear
Temperature [K]: Viscosity [kg/(m s)]:
1 275,15 1,728e-05
2 281,65 1,759e-05
3 288,15 1,790e-05

43. 33
0
100
200
300
400
500
600
700
800
900
1000
0 2 4 6 8 10 12 14 16 18
velocità u [m/s]
quotaz[m] ingresso (log-law)
aria come da Tab. 2-3
aria come [2]
Figura 2-3 – Profili del vento ottenuti con diverse caratteristiche dell’aria. In rosso aria come da
tabella 2-3; in verde aria come da tabella 2-5.
Osservando la figura 2-2 non si notano sostanziali migliorie tra vecchie e nuove
impostazioni per le caratteristiche dell’aria, ma il considerare le relazioni tra le
variabili fisiche tipiche di un’atmosfera adiabatica secca sembra tuttavia la scelta più
opportuna e tutte le simulazioni eseguite sono state effettuate con le impostazioni
sulle caratteristiche fisiche dell’aria come in tabella 2-3.
2.5 Valutazione del flusso a ridosso delle pareti. Flusso
su superfici lisce.
È importante valutare con precisione il flusso a ridosso delle superfici o pareti
solide a contatto col flusso, in quanto questo influenza il flusso all’interno del
dominio. Il codice FLUENT, per calcolare velocità e temperatura del fluido nelle
celle adiacenti le pareti, fa ricorso a delle formule semi-empiriche e le due modalità
di simulazione sono le seguenti:
Wall functions
Two Layers zonal Model
Le “wall functions” sono a loro volta suddivise in “standard wall functions” e
“non-equilibrium wall functions”, portando a tre le scelte possibili, descritte nei
paragrafi seguenti.

44. 34
2.5.1 Standard Wall Functions.
Le Standard Wall Functions implementate in FLUENT sono basate sugli studi di
Launder e Spalding [3], e sono state ampiamente utilizzate in campo industriale.
Le “standard wall functions” sono un insieme di equazioni semi-empiriche che
descrivono il flusso in prossimità delle pareti. Esse permettono il calcolo di tutte le
grandezze necessarie alla valutazione del flusso interno. In particolare, per la cella in
prossimità della parete viene considerato valido il profilo di velocità logaritmico
(log-law), che per flusso su pareti lisce risulta:
( )*ln
1
* Eyu
κ
= (2.22)
dove u* e y* sono due parametri adimensionali calcolati utilizzando il modello k-
ε con
a)
ρτ
µ
/
*
2/14/1
w
kCu
u
⋅⋅
= b)
µ
ρ µ ykC
y
⋅⋅⋅
=
2/14/1
* . (2.23)
Come si nota, le standard wall functions utilizzano i gruppi adimensionali u* e y*
piuttosto che u+
e y+
. La legge logaritmica (1.20), valida per y*>30 ~ 60, in
FLUENT, viene impiegata per y*>11,225.
Quando la griglia costruita in prossimità della parete è tale che, per la simulazione
considerata, il parametro y* sia minore di 11,225, nelle celle adiacenti le pareti,
FLUENT applica una legge valida per il sottostrato viscoso che può essere scritta
nella forma seguente:
** yu = (2.24)
Questa situazione è tuttavia da evitare [3], e si deve costruire la griglia in maniera
tale che la prima cella ricada nella zona dove è valida la (2.22). Si può notare che la
legge (2.22) ed una analoga per la temperatura qui non riportata, sono basate sulla y*
piuttosto che sulla y+
. Le due grandezze adimensionali sono tuttavia coincidenti nel
caso di strato limite turbolento in condizione di equilibrio, ovvero quando la
produzione di energia cinetica turbolenta è uguale alla sua dissipazione (Gk=ρ ε).
2.5.2 Non-equilibrium wall functions.
Le “Non-equilibrium Wall Functions” tengono conto dei gradienti di pressione
paralleli alla parete. Esse sono quindi adatte a tutte quelle situazioni in cui si hanno
dei grandi gradienti di pressione in prossimità delle pareti,. Le “Non-equilibrium
Wall Functions” sono indicate nelle simulazioni di flussi su ostacoli particolarmente
complessi, che comportano distacchi della vena fluida o, comunque, tutte le volte in

45. 35
cui si hanno degli elevati gradienti di pressione, e ciò vale anche nella simulazione
dello SLA..
2.5.3 Two-Layer zonal model.
Con questa opzione FLUENT risolve con un particolare modello di turbolenza
(semplificato) il flusso all’interno del sottostrato viscoso e nello strato di
sovrapposizione (buffer layer), mentre utilizza negli strati superiori il modello di
turbolenza scelto. L’uso di questo approccio comporta l’infittimento della griglia in
vicinanza delle pareti e non è adatto allo studio dello SLA.
2.6 Valutazione del flusso a ridosso delle pareti. Flusso
su superfici rugose.
Per simulare strati limite sensibili all’effetto della rugosità della parete, il codice
FLUENT utilizza delle formule proposte da Cebeci e Bradshaw [3] basate sui dati
raccolti da Nikuradse.
La legge implementata in FLUENT per tenere conto degli effetti della rugosità è
la seguente:
B
yu
E
uu
w
∆−




 ⋅⋅
⋅=
⋅
µ
ρ
κρτ
*
ln
1
/
*
(2.25)
analoga alla equazione (1.27), dove u* è la stima della velocità d’attrito, ricavata
dal codice FLUENT mediante la relazione
2/14/1
* kCu ⋅= µ (2.26)
Per descrivere la rugosità di una parete, il codice FLUENT utilizza due parametri,
definiti altezza di rugosità (Roughness Height) RH, e costante di rugosità (Roughness
Constant) RC. La funzione di rugosità ∆B che compare nella (2.25), viene valutata in
base alla Roughness Height adimensionalizzata RH+
ed in base a RC. Si definisce
infatti il gruppo adimensionale RH+
:
µ
ρ *uRH
RH
⋅⋅
=+
. (2.27)
Secondo una classificazione proposta da Cebeci e Bradshaw, lo strato limite
turbolento si può suddividere in tre regimi diversi, che si differenziano per il valore
assunto dalla rugosità adimensionalizzata h+
.

46. 36
Flusso idrodinamicamente liscio (h+
< 3÷5)
Flusso di transizione (3÷5 < h+
< 70÷90)
Flusso idrodinamicamente rugoso (h+
> 70÷90)
In accordo con tale teoria, gli effetti della rugosità sullo strato limite sono
trascurabili quando il regime è idrodinamicamente liscio, aumentano in maniera
graduale quando il regime è di transizione, per poi raggiungere il regime di flusso
idrodinamicamente rugoso, nel quale sono particolarmente importanti. Per valori di
h+
minori di 4 lo strato limite che s’instaura ricade nel regime tipico delle pareti lisce
(Smooth Flow).
Anche ne codice FLUENT viene utilizzata la suddetta classificazione. e per
stimare il valore di ∆B vengono utilizzate le seguenti espressioni:
Per flusso aerodinamicamente liscio (RH+
< 2,25):
0=∆B (2.28)
Per il regime di transizione (2,25 < RH+
< 90):
( )[ ]811,0ln4258,0sin
75,87
25,2
ln
1
−⋅×





⋅+
−
=∆ ++
+
RHRHRC
RH
B
κ
(2.29)
Per flusso aerodinamicamente rugoso (RH+
> 90):
( )+
⋅+=∆ RHRCB 1ln
1
κ
(2.30)
La costante di rugosità RC dipende dal tipo di rugosità e dalla geometria delle
asperità. RC può essere visto come un fattore di forma delle asperità, mentre RH un
fattore dimensionale. Il valore di riferimento utilizzato nel codice FLUENT è 0,5,
valore determinato in maniera tale che, usando il modello di turbolenza k-ε,
venissero riprodotti i risultati sperimentali ottenuti da Nikuradse.
Per rugosità dovuta ad asperità diverse da quelle studiate da Nikuradse la costante
RC può essere modificata, mantenendo valori compresi tra 0,5 e 1, ma non esiste
alcuna regola che guidi la sua scelta.
Facendo riferimento alle formule utilizzate da FLUENT per valutare ∆B, si può
fare una stima del rapporto z0/RH, parametro utile per l’impostazione delle
simulazioni. Infatti, confrontando la (1.29) con la (2.30), e quindi solo per RH+
>90,
risulta:

47. 37
+
⋅+=⋅ RHRCE 1*Re , ed essendo 1>>⋅ +RHRC
+
⋅≈⋅ RHRCE *Re
µ
ρ
µ
ρ **0 uRH
RC
uz
E
⋅⋅
⋅≈
⋅⋅
⋅
RHRCzE ⋅≈⋅ 0
RH
E
RC
z ⋅≈0 (2.31)
tenendo conto che E è una costante, agendo su RC si può pertanto modificare il
rapporto z0/RH. Queste considerazioni sono state utilizzate nelle simulazioni per
fissare i valori di primo tentativo dei parametri RH e RC dei terreni caratterizzati da
lunghezza di rugosità z0.
2.7 Costruzione della griglia in prossimità delle pareti.
Quando si utilizzano le Standard Wall Functions si devono realizzare le celle
adiacenti le pareti facendo in modo che, nella particolare simulazione, il valore di y+
sia compreso nel campo 30÷130. In questa maniera si fa in modo che le celle
confinanti con le pareti siano già posizionate in una zona del flusso dove è valida la
legge logaritmica (2.22), o la (2.25) se si tiene conto della rugosità della parete. Lo
scopo delle Wall Functions è proprio quello di risparmiare risorse di calcolo
“saltando” la zona dello strato limite in cui non è valida la legge logaritmica, e
proprio per questo motivo occorre evitare di ottenere per la y+
.valori inferiori a 30
Con il two-layer zonal model, invece, dal momento che questo calcola il flusso
all’interno del sottostrato viscoso e dello strato di sovrapposizione, bisogna costruire
una griglia caratterizzata da valori di y+
di 4∼5 (idealmente 1) delle celle adiacenti le
pareti e avere almeno una decina di celle all’interno della regione vicino alle pareti
affetta dalla viscosità del fluido (Rey<200), [3].
Le diverse esigenze sul valore di y+
possono cadere in contrasto con un ulteriore
richiesta a cui devono rispondere le celle adiacenti il terreno, che è quella di avere
un’altezza almeno doppia rispetto all’altezza delle asperità [3] intesa come RH.
Quando le pareti sono delle superfici notevolmente rugose, come i terreni, le due
richieste non possono mai essere verificate contemporaneamente.
In [2] le griglie relative al flusso sulla collina bidimensionale sono state realizzate
soddisfacendo le richieste su y+
, e si è notato che, per mantenere tale parametro a
valori leggermente superiori a 30, si deve costruire la cella confinante col terreno con
un altezza di 0,002m. Nel lavoro presente si sono messe a confronto le due

48. 38
metodologie di discretizzazione del dominio, la prima che permette di soddisfare le
richieste su y+
(altezza 0,002m), la seconda che prevede le prime celle con altezza
almeno doppia di RH.
In quest’ultimo caso, cioè per avere un’altezza h della cella adiacente il terreno
almeno doppia del valore di RH, e, contemporaneamente, un RH corrispondente alla
una lunghezza di rugosità z0, si può ottenere un primo valore orientativo per le
diverse grandezze in esame.
Se, ad esempio, si sta studiando un terreno con lunghezza di rugosità z0=0,03m,
fissiamo arbitrariamente RC a 1 (valore massimo in FLUENT 6) e, in base alla
(2.31):
m
m
RC
zE
RH 2943,0
1
03,081,90
=
⋅
=
⋅
≈ (2.32)
mRHh 5886,02 =⋅≥ (2.33)
Quindi, se per mantenere y+
su valori dell’ordine di 30÷130 si era visto che h
doveva assumere un valore di circa 0,002m, per soddisfare la seconda ipotesi h deve
essere scelto pari a 0,6m, valore notevolmente diverse e che permette una notevole
diminuzione dei punti della discretizzazione. In tabella 2-6 sono riportati i valori di
RH e h calcolati per due lunghezze di rugosità.
z0 RH h minimo
0,01m 0,0981m 0,1962m
0,03m 0,2943m 0,5886m
Tabella 2-6 – Valori di RH e h calcolati in base alla (2.31), considerando RC=1, E=9,81 e h minimo
doppio di RH.
Sono state svolte delle simulazioni con h e RH come in tabella 2-6 (RC=1), ed i
risultati sono stati messi a confronto con quelli di simulazioni effettuate con h=
0,002m e RH come da tabella 2-6 (RC=1), relativamente a due valori di rugosità z0,
pari a 0,01m e 0,03m

49. 39
0
100
200
300
400
500
600
700
800
900
1000
0 2 4 6 8 10 12 14 16 18
velocità u [m/s]
quotaz[m]
ingresso
dopo 6 km, h 0,002m
dopo 6 km, h 0,2m
dopo 4 km, h 0,002m
dopo 4 km, h 0,2m
Figura 2-4 – z0 0,01m; u* 0,588m/s, profili del vento ottenuti con RC=1 e RH=0,0981m.
0,001
0,01
0,1
1
10
100
1000
0 2 4 6 8 10 12 14 16 18
velocità u [m/s]
quotaz[m]
ingresso
dopo 6 km, h 0,002m
dopo 6 km, h 0,2m
dopo 4 km, h 0,002m
dopo 4 km, h 0,2m
Figura 2-5 – z0 0,01m; u* 0,588m/s, stessi profili del vento di figura 2-4, ma su piano semi-
logaritmico.

50. 40
Dalle figure 2-4 e 2-5 si possono trarre alcune considerazioni, la più importante
delle quali è che se con un’altezza della prima cella h=0,2m si riesce a simulare
meglio il vento vicino al terreno, in una zona compresa sotto il primo metro di quota,
con h=0,002m l’errore commesso è minore per una altezza dal suolo compresa tra 10
e 100 metri, la più interessante per lo sfruttamento dell’energia eolica. Infatti, le
attuali turbine eoliche hanno rotori di circa 50-80 m di diametro e asse di rotazione
posizionato ad una altezza dal suolo di 60-90 m.
Di seguito sono riportati risultati analoghi alle fig. 2-4 e 2-5 ma per lunghezza di
rugosità 0,03m. Per le impostazioni generali delle simulazioni si rimanda ai paragrafi
successivi.
I profili mostrati nelle figure 2-4, 2-5, 2-6 e 2-7 si riferiscono a valori di RC
unitari e RH calcolato come da tabella 2-6. In simulazioni successive, i cui risultati
sono illustrati nel paragrafo 2.11, si è notato come, diminuendo i valori di RC e RH
si ottengono delle situazioni in cui il profilo del vento si mantiene più vicino a quello
logaritmico impostato in ingresso, soprattutto nello strato tra 10 e 100 metri di quota,
individuato come lo strato di maggiore interesse.

51. 41
z0 0,03m
u* 0,65m/s
0
100
200
300
400
500
600
700
800
900
1000
5 7 9 11 13 15 17
velocità u [m/s]
quotaz[m]
ingresso
dopo 6km, h 0,002m
dopo 6km, h 0,6m
dopo 4km, h 0,002m
dopo 4km, h 0,6m
Figura 2-6 – z0 0,03m; u*=0,65m/s; profili del vento ottenuti con RC=1, RH=0,2943m.
z0 0,03m
u* 0,65m/s
0,001
0,01
0,1
1
10
100
1000
0 2 4 6 8 10 12 14 16 18
velocità u [m/s]
quotaz[m]
ingresso
dopo 6km, h 0,002m
dopo 6km, h 0,1m
dopo 6km, h 0,6m
dopo 4km, h 0,002m
dopo 4km, h 0,1m
dopo 4km, h 0,6m
Figura 2-7 – z0 0,03m; u*=0,65m/s; stessi profili di figura 2-6 su piano semi-logaritmico.

52. 42
2.8 Scelta delle costanti del modello di turbolenza
standard k-εεεε.
Come illustrato nel paragrafo 2.2, il modello di turbolenza standard k-ε è
caratterizzato da sei costanti il cui valore di default in FLUENT è riportato in tabella
2-1. Sebbene i valori di riferimento siano adatti alla maggior parte delle comuni
applicazioni ingegneristiche, in particolari situazioni una scelta opportuna delle
costanti del modello può migliorare i risultati delle simulazioni, specialmente nella
previsione di caratteristiche riguardanti la turbolenza.
Da misure effettuate sullo SLA a 10m di quota, si sono trovati valori di k/u*2
di
5,77 circa. In base alla (2.35) si è cambiato il valore di Cµ.
03,0
77,5
1*
222
≈





=





=
k
u
Cµ (2.35)
In condizione di stazionarietà e strato limite completamente sviluppato, dalla
equazione della TKE (2.10)si ottiene:
ρ ε=Gk
per Gb=0,
sostituendo i valori di Gk e Gb, con Gk, k ed ε espressi secondo le wall functions,
nell’equazione della TDR (2.15) si arriva alle seguente relazione che lega le costanti
del modello.
µεσ
κ
C
CC
2
12 =− (2.36)
In questa equazione il valore di Cµ, è fissato, come detto in precedenza, ed è
preferibile lasciare costante anche il valore di σε (1,3), mantenendo a valori prossimi
all’unità anche i numeri di Prandtl turbolenti per le TKE e TDR.
Le nuove costanti del modello sono riportate in tabella 2-6.
Costanti del modello standard k-ε, valori modificati
Cµ C1 C2 σκ σε Prt
0,03 1,44 2,223 1 1,3 0,85
Tabella 2-7 – Valori modificati delle costanti del modello standard k-ε.
I valori delle costanti di tabella 2-7 sono stati utilizzati in tutte le simulazioni, sia
nel caso bidimensionale che nel tridimensionale.

53. 43
2.9 Flusso su terreni pianeggianti.
Le simulazioni su terreni piani sono servite per ricercare i valori dei parametri del
codice che descrivono meglio il comportamento sui terreni reali. In particolare si
sono ricercati i valori dei parametri di rugosità RH e RC da associare ad una precisa
lunghezza di rugosità z0. Se ad un terreno corrisponde una data lunghezza di rugosità,
in condizioni di stabilità neutra, il profilo ottenuto con la legge logaritmica e
impostato all’ingresso del dominio, deve rimanere immutato fino all’uscita se
vengono assegnati i valori corretti dei vari parametri. Si sono costruiti quindi dei
domini di simulazione lunghi 6km e alti 1km che permettessero allo strato limite in
ingresso di adattarsi alle impostazioni del codice, verificando in tal modo se i
parametri RH e RC, le relazioni densità-temperatura e infittimento della griglia
vicino al terreno fossero quelli corretti per lo strato limite impostato in ingresso.
Alcuni risultati sono già stati riportati nelle figure da 2-4 a 2-7.
Si sono studiati due terreni pianeggianti, con lunghezza di rugosità pari a 0,01 e
0,03 A questi valori di z0 corrispondono ben determinati tipi di terreno, come si può
vedere dalla tabella 1-3.
Il valore di z0=0,01m è stato considerato in [7] per delle simulazioni
bidimensionali su una collina avente rapporto H/L di 0,4 e per un ostacolo
trapezoidale ed i risultati ottenuti sono utili per eventuali confronti. Il valore di z0
pari a 0,03m è invece tipico dei terreni caratteristici di una zona, la collina di
Askervein, nelle isole Ebridi, per la quale sono disponibili molti risultati
sperimentali, ottenuti nel corso di una importante campagna di misure descritta in
[6].
2.9.1 Discretizzazione del dominio di calcolo e condizioni al
contorno.
La geometria utilizzata è un rettangolo di lunghezza 6 km e altezza dal suolo 1
km. Si suppone che il vento a partire da una quota di 1 km rimanga invariato, ovvero
si è supposto che il vento all’altezza dal suolo di 1 km sia geostrofico. Nella figura 2-
8 è rappresentata la griglia utilizzata per lo studio dello SLA su terreni pianeggianti.

54. 44
1 km
60 ∆y
6 km - 300 ∆x
20 m
h
altezza prima cella
Totale celle 60 x 300 = 18 000 celle
particolare
Figura 2-8 – Griglia per i terreni pianeggianti, dominio completo e particolare vicino al bordo
d’ingresso.
La griglia realizzata, rappresentata in figura 2-8, è costituita da celle aventi
dimensione orizzontale di 20m e dimensione verticale di altezza progressivamente
variabile,a partire da un’altezza minima h della cella adiacente il terreno, fino a
ricoprire con 60 celle la dimensione verticale complessiva del dominio di calcolo. Si
sono costruite diverse griglie, che differivano per il valore attribuito all’altezza della
cella adiacente il terreno. Il valore minimo assegnato ad h è stato di 0,002m, mentre
la massima altezza h considerata è stata 0,6m.

55. 45
Il dominio di calcolo risulta dunque composto da 18000 celle, numero
abbondantemente minore di quello consentito dalla potenzialità di calcolo del PC a
disposizione, ma in tal modo sono stati utilizzati gli stessi parametri di costruzione
della griglia che verranno poi usati anche nel caso tridimensionale.
Geostrofico
Terreno
Ingresso
Uscita
x
y
Figura 2-9 – Nomi assegnati ai quattro bordi delimitanti il dominio di calcolo.
Ai quattro bordi delimitanti il dominio, visibili in figura 2-9, sono assegnati dei
nomi significativi e le condizioni al contorno utilizzate per ciascuno di essi sono
elencate di seguito.
Ingresso – Velocity Inlet
La condizione al contorno Velocity Inlet necessità di alcune specifiche. Per essa è
infatti necessario definire la velocità, la temperatura, l’energia cinetica turbolenta tke
e la sua velocità di dissipazione tdr. Sul bordo d’ingresso le grandezze appena citate
variano notevolmente con la quota. Per risolvere il problema, il codice FLUENT
permette di imporre dei file contenenti i profili da assegnare, creati secondo la
procedura descritta in appendice I e rispondenti a ben precise funzioni illustrate nel
paragrafo successivo 2.9.2.
Terreno – Wall
Anche la condizione al contorno wall necessita di alcune specifiche. Al terreno è
stata assegnata una temperatura statica di 288,15 K insieme coi valori dei diversi
parametri di rugosità RH e RC il cui significato è già stato discusso.
Geostrofico – Velocity Inlet oppure Symmetry
Per quanto concerne la scelta della condizione al geostrofico tra velocity inlet o
symmetry, i due tipi di condizioni al contorno portano quasi agli stessi risultati, come

56. 46
si vede dalla figura 2-10, con una previsione migliore del campo di moto da parte
della condizione symmetry in prossimità del geostrofico stesso, a 1000m di quota.
z0 0,01m
u* 0,588 m/s
0
100
200
300
400
500
600
700
800
900
1000
0 2 4 6 8 10 12 14 16 18
velocità u [m/s]
quotaz[m]
ingresso (log-law)
h 0,1m RH 0,03m RC 0,7 geostrofico vel-inlet
h 0,1m RH 0,03m RC 0,7 geo.symmetry
Figura 2-10 – Confronto tra profili in uscita (dopo 6km) nel caso di geostrofico velocity inlet e
symmetry.
Uscita – Outflow
La condizione al contorno outflow viene impiegata quando, prima della
simulazione, non si conoscono gli andamenti di velocità e pressione nel bordo di
uscita. Questa viene applicata in maniera appropriata solamente quando in prossimità
dell’uscita ci si aspetta di trovare delle condizioni di flusso completamente
sviluppato, gradienti normali al bordo di uscita nulli, ad eccezione dei gradienti di
pressione. La condizione al contorno outflow non è indicata allo studio di flussi
comprimibili. Un’alternativa alla condizione al contorno outflow poteva essere la
pressure outlet che prevede però l’assegnazione della pressione statica. Per ulteriori
chiarimenti si rimanda al capitolo 6 di [3] che tratta, appunto, delle condizioni al
contorno applicabili col codice FLUENT.

57. 47
2.9.2 Profili in ingresso, andamento di alcune grandezze con la
quota.
Come detto nel paragrafo precedente, al bordo di ingresso è stata assegnata la
condizione al contorno di tipo Velocity Inlet. Ciò comporta il dover assegnare in tutti
i punti del bordo di ingresso, i valori di velocità, temperatura, TDR e TKE. I primi
tre parametri, Velocità, temperatura e TDR, sono stati assegnati come profili, con
delle leggi che tengono conto della loro notevole variazione con la quota. Le
equazioni in base alle quali si sono costruiti i files leggibili dal codice sono la (2.37),
(2.38) e la (2.39), esse sono analoghe ai profili in ingresso utilizzati in [2] ed in [8].
La procedura utilizzata per costruire un file di profilo importabile con FLUENT è
descritta in Appendice I.
In base alla (2.40) la TKE dovrebbe rimanere costante con la quota, e ciò è stato
considerato in [2] ed in [8]. Nella realtà questo non si verificato, come si vede dalla
figura 3.3 di [12] e dalla figura 3 di [10], relative a risultati sperimentali. Una
migliore previsione della turbolenza e, in generale, dei risultati ottenuti, potrebbe
dipendere proprio da una più accurata scelta dei profili di TKE e TDR all’ingresso.
Inoltre, l’impostazione della TKE tramite l’equazione (2.40) comporta una
sovrastima della viscosità turbolenta man mano che la quota aumenta. Durante il
calcolo il codice FLUENT valuta ad ogni iterazione il rapporto µt/µ e se questo
rapporto in ogni cella è maggiore di un limite fissato il codice lo segnala come errore
e assegna automaticamente un valore massimo di µt alle celle nelle quali la viscosità
turbolenta risulta troppo elevata. Tutto ciò comporta un rallentamento del calcolo ed
anche per questo motivo è consigliabile definire un profilo di tke più rispondente alla
realtà, e quindi decrescente con la quota.
Di seguito sono elencati i profili assegnati in ingresso nelle simulazioni del
presente lavoro.
Velocità, componente media orizzontale:






=
0
ln
*
)(
z
zu
zU
κ
(2.37)
Temperatura, atmosfera adiabatica secca:
zTzT ad ⋅Γ+= 0)( (2.38)

58. 48
TDR:
z
u
z
3
*1
)(
κ
ε = (2.39)
TKE:
2
*
1
u
C
k ⋅=
µ
(2.40)
Per avere un’idea di come possano essere modificati i profili in ingresso si riporta
un insieme di profili assegnato in alcuni lavori scientifici.
In [13] sono stati utilizzati i seguenti profili di ingresso:
( ) 





=
0
ln
*
z
zu
zU
κ
( )
2
2
1
*














−=
BLL
z
C
u
zk
µ
con LBL spessore dello SLA
( ) 





+=
obukhovLz
u
z
41*3
κ
ε con Lobukhov=1000m
In [14] sono illustrati altri profili d’ingresso più o meno analoghi a quelli utilizzati
da [13].
2.10 Condizioni operative.
Tra i parametri da fissare prima di avviare le simulazioni numeriche vi sono le
condizioni operative, che determinano i valori di riferimento rispetto ai quali valutare
le variabili di calcolo. Come pressione operativa si è scelto un valore pari a 101325
Pa, assegnata al punto di coordinate x=0 e y=0, posto quindi sull’ingresso.
Si è inoltre imposto che il codice tenesse conto della accelerazione di gravità, pari
a -9,8066 m/s2
lungo la direzione y. La temperatura operativa assegnata è pari a
278,39 K, temperatura prevista a 1000m di quota secondo il profilo dato dalla (2.19).
E’ stata inoltre imposta una densità operativa, in tal modo il codice FLUENT non ne
aggiorna il valore ad ogni iterazione. Ad essa è assegnato il valore di 1,1239 kg/m3
,
densità prevista a 1000m di quota secondo il profilo dato dalla (2.21).

59. 49
CONDIZIONI OPERATIVE
Pressione operativa 101325 Pa Gravità:
Posizione di riferimento per la pressione X 0 m/s2
Y -9,8066 m/s2
X 0 m Temperatura operativa: 278,39 K
Y 0 m Densità operativa : 1,1239 kg/m3
Tabella 2-8 – Condizioni operative per le simulazioni.
Solo a seguito di diverse simulazioni, si è notato come con una densità operativa
di 0 kg/m3
si riesca a prevedere con buona precisione l’andamento della pressione
con la quota. Nel successivo paragrafo sono illustrati i risultati numerici con densità
operativa pari a 1,1239 kg/m3
e si può vedere, figura 2-12c, come non si riesca a
prevedere la corretta diminuzione di pressione con la quota.
2.11 Risultati numerici delle simulazioni su superfici
piane.
In figura 2-11 sono rappresentati i profili di velocità in uscita dal dominio di
calcolo ottenuti con diversi parametri della rugosità del terreno (RH e RC). Il
risultato ideale è quello in cui il profilo del vento in uscita rimane uguale a quello
impostato in ingresso (legge logaritmica).

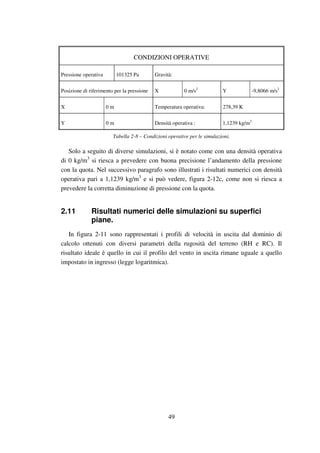
60. 50
z0 0,01m
u* 0,588 m/s
0
100
200
300
400
500
600
700
800
900
1000
0 2 4 6 8 10 12 14 16 18
velocità u [m/s]
quotaz[m]
ingresso (log-law)
h0,1m RH 0,01m RC 0,5
h0,1m RH 0,01m RC 0,3
h0,1m RH 0.03m RC 0.7
h0,1m RH 0.03m RC 0.5
h0,1m RH 0.03m RC 0.3
h0,2m RH 0,98m RC 1
Figura 2-11 – Profili in uscita con diversi valori di RH e RC, lunghezza di rugosità 0,01m. Le curve
per altezza della prima cella h 0,1 m sono sovrapposte. La curva ottenuta con altezza della prima
cella h 0,2 m e valori di RH e RC valutati secondo la teoria di Bradshaw si discosta ulteriormente dal
profilo in ingresso.
z0 0,01m
u* 0,588 m/s
0,1
1
10
100
1000
0 2 4 6 8 10 12 14 16 18
velocità u [m/s]
quotaz[m]
ingresso (log-law)
h0,1m RH 0,01m RC 0,5
h0,1m RH 0,01m RC 0,3
h0,1m RH 0.03m RC 0.7
h0,1m RH 0.03m RC 0.5
h0,1m RH 0.03m RC 0.3
h0,2m RH 0,098m RC 1
Figura 2-12 – Stessi profili di figura 2-10. La scala delle quote è logaritmica per mettere in evidenza
l’effetto dei parametri RH e RC sul flusso in prossimità della parete.

61. 51
Nella figura 2-12 sono rappresentati su piano semi logaritmico gli stessi profili di
velocità di figura 2-11. Dai profili del vento rappresentati in figura 2-11 si vede come
i valori di h, RH e RC calcolati secondo la teoria di Bradshaw prevedano in maniera
corretta la velocità vicino al suolo ma non riescano a fare altrettanto negli strati più
alti. Viceversa, diminuendo i valori di RH e RC non è più prevista in maniera
corretta la velocità al suolo ma migliora la previsione della velocità a quote maggiori.
In figura 2-13 a, b, c sono rappresentati i profili di temperatura, densità, pressione
che si osservano in uscita dal dominio di calcolo, confrontati con quelli relativi alla
atmosfera adiabatica. L’energia cinetica turbolenta di figura 2-13 d è confrontata col
profilo impostato in ingresso. Le figure 2-13 sono riferite alle simulazioni per
z0=0,01m, i parametri riguardanti la rugosità (RH, RC e z0) non influenzano
significativamente le grandezze mostrate in figura 2-13, per questo motivo si è scelto
di non mostrare, in grafici analoghi al 2-13, i risultati relativi a lunghezza di rugosità
0,03m ed a diversi valori di RH e RC.
L’andamento di temperatura statica e densità dell’aria sono rispettati, il modello
non prevede però con esattezza la giusta diminuzione di pressione con la quota, e,
soprattutto, si rileva inefficace nel prevedere e mantenere il giusto valore di energia
cinetica turbolenta. È da osservare che anche nelle simulazioni mostrate in [10] non è
stato possibile prevedere correttamente le grandezze relative alla turbolenza.
Per la lunghezza di rugosità z0=0,03m, si sono effettuate diverse simulazioni su
superfici piane. I domini studiati sono stati tre, caratterizzati da diverse altezze h
delle celle confinanti col terreno. Le altezze h considerate sono state 0,6m, 0,1m e
0,002m. In figura 2-14 sono mostrati i profili di velocità ottenuti all’uscita del
dominio di calcolo per le tre diverse altezze, mantenendo i parametri di rugosità RH
e RC rispettivamente a 0,2943m e 1, quelli di tabella 2-6.
Variando i valori di RH e RC rispetto a quelli di primo tentativo di tabella 2-6, si è
cercato di ottenere dei profili di velocità che approssimassero meglio la legge
logaritmica
In figura 2-15 sono mostrati cinque profili di velocità, in uscita dal dominio, dopo
6 km dall’ingresso, relativi a domini con altezza della prima cella h di 0,6m.
Il profilo che approssima maggiormente la legge logaritmica, vicino alle pareti, è
quello a cui corrisponde RH 0,03m e RC 1 mentre con RH 0m il profilo è ancora più
vicino alla legge logaritmica per una quota compresa tra 10 e 100m ma si discosta
notevolmente per quote inferiori.
La figura 2-16 è analoga alla 2-15 ma relativa ad un dominio con altezza della
prima cella h di 0,1m, la figura 2-17 è invece relativa al dominio caratterizzato da h
di 0,002m.

62. 52
In seguito ai risultati esposti circa le simulazioni su terreni piani si può vedere che
domini con h di 0,002m permettono di simulare bene il flusso per una quota
nell’intervallo 10m÷100m, ma non si riesce a valutare la velocità desiderata per le
celle prossime al terreno.
Domini con h 0,6m e 0,1m permettono di stimare invece in maniera più accurata
la velocità in prossimità del terreno ma portano a sottostimare la velocità del vento
alle quote d’interesse, dei miglioramenti si possono ottenere variando i parametri RH
e RC.
La scelta più appropriata sembra quella di costruire domini di calcolo discretizzati
con h di 0,002m circa, in maniera da soddisfare la condizione sull’y+
.
Nonostante le simulazioni eseguite su terreni piani, quando lo studio si è portato
su terreni complessi, sia 2D che 3D (vedi capitoli successivi), domini con h di
0,002m hanno portato a divergenza del processo iterativo. Si sono ottenuti risultati
convergenti solo quando i domini erano discretizzati con celle adiacenti il terreno
almeno alte 5 cm. Ciò a portato a trascurare, per i terreni complessi, domini di calcoli
caratterizzati da bassi valori di h. Per la simulazione 2D su Askervein (vedi capitolo
3) si è optato per un dominio avente h di 0,1m, mentre per la simulazione 3D su
Askervein (capitolo 4) si è invece utilizzato un dominio con h di 0,6m.

63. 53
Temperatura
0
100
200
300
400
500
600
700
800
900
1000
276 278 280 282 284 286 288 290
T [K]
quotaz[m]
Densità
0
100
200
300
400
500
600
700
800
900
1000
1,1000 1,1500 1,2000 1,2500
ρ [kg/m
3
]
quotaz[m]
Pressione assoluta
0
100
200
300
400
500
600
700
800
900
1000
85000 90000 95000 100000 105000
p [Pa]
quotaz[m]
TKE
0
100
200
300
400
500
600
700
800
900
1000
0 0,5 1 1,5 2 2,5
k [m2/s2]
quotaz[m]
Figura 2-13 – Andamento di temperatura a), densità b), pressione c) ed energia cinetica turbolenta k
d) con la quota z. Confronto tra risultati in uscita (6 km dall’ingresso), in rosso, e atmosfera
adiabatica, in blu, per i primi tre grafici. Per l’energia cinetica turbolenta TKE è invece
rappresentato il confronto tra il valore impostato in ingresso, in blu, e il profilo che si osserva in
uscita dal dominio, in rosso.

64. 54
z0 0,03m u* 0,65m/s
modello standard k-eps .
RH 0,2943m RC 1
profili valutati diopo 4 km dall'ingresso
0,001
0,01
0,1
1
10
100
1000
0 2 4 6 8 10 12 14 16 18
velocità u [m/s]
quotaz[m]
ingresso
h 0,6m
h 0,1m
h 0,002m
Figura 2-14 – Profili del vento stimati dopo 4 km dall’ingresso, per RH 0,2943m e RC unitario.
h 0,6m
z0 0,03m
u* 0,65m/s
profili valutati all'uscita del dominio
(dopo 6 km)
0,1
1
10
100
1000
0 2 4 6 8 10 12 14 16 18
velocità [m/s]
quotaz[m]
ingresso
RH 0,2943m; RC 1
RH 0,1m; RC 1
RH 0,03m; RC 1
RH 0,03m; RC 0,5
RH 0m; RC 0,5
Figura 2-15 – Profili del vento per h 0,6m e diversi valori di RH (RC=1).

65. 55
h 0,1m
z0 0,03m
u* 0,65m/s
profili a 4 km dall'ingresso
0,1
1
10
100
1000
0 2 4 6 8 10 12 14 16 18
velocità [m/s]
quota[m]
ingresso
RH 0,2943m; RC 1
RH 0,05m; RC 1
RH 0,03m; RC 1,5
RH 0,03m; RC 1
RH 0,03m; RC 0,5
RH 0m; RC 1
Figura 2-16 – Profili del vento valutati per h 0,1m e diversi valori di RH e RC).
h 0,002m
z0 0,03m
u* 0,65m/s
profili valutati a 4 km dall'ingresso
0,001
0,01
0,1
1
10
100
1000
0 2 4 6 8 10 12 14 16 18
velocità [m/s]
quota[m]
ingresso
RH 0,2943m RC 1
RH 1m RC 1
RH 10m RC 2
RH 20m RC 2
RH 20m RC 4
Figura 2-17 – Profili relativi ad h 0,002m.

66. 56
2.12 Considerazioni sulla densità operativa
Come scritto nel paragrafo 2.10, sebbene tutte le simulazioni, sia bidimensionali
che tridimensionali, siano state svolte imponendo una densità operativa di 1,1239
kg/m3
, si è osservato, successivamente, che con una densità operativa di 0 kg/m3
si
riesce a prevedere in maniera corretta l’andamento della pressione con la quota,
come si può vedere dalla figura 2-14 analoga alla 2-13 ma ottenuta con densità
operativa nulla.
a) Temperatura
0
100
200
300
400
500
600
700
800
900
1000
276 278 280 282 284 286 288 290
T [K]
quotaz[m]
atmosfera
adiabatica
risultati
numerici
b) Densità
0
100
200
300
400
500
600
700
800
900
1000
1,1000 1,1500 1,2000 1,2500
ρ [kg/m3
]
quotaz[m]
atmosfera
adiabatica
risultati
numerici
c) Pressione assoluta
0
100
200
300
400
500
600
700
800
900
1000
85000 90000 95000 100000 105000
p [Pa]
quotaz[m]
atmosfera
adiabatica
risultati
numerici
d) TKE
0
100
200
300
400
500
600
700
800
900
1000
0 0,5 1 1,5 2 2,5 3
k [m2
/s2
]
quotaz[m]
ingresso
uscita
Figura 2-18 – Profili analoghi a quelli di figura 2-13 ottenuti con densità operativa di 0 kg/m3
.

67. Capitolo 3 Simulazioni 2D sulla collina di Askervein.
3.1 Vento sopra terreni collinari.
La presenza di ostacoli naturali, di vegetazione, ed in generale l’orografia del
terreno, influenzano il campo di moto dei flussi atmosferici all’interno dello SLA.
Un caso semplice, ma molto importante, è quello relativo ad una collina isolata
situata all’interno di un territorio pianeggiante che, quando è investita dal vento,
determina un aumento di velocità del flusso d’aria presso la sua sommità e attorno ai
suoi versanti. A valle della collina inoltre si forma una scia, intesa come quella zona
nella quale è presente una diminuzione della componente di velocità parallela al
vento indisturbato, che può occupare uno spazio più o meno grande in rapporto
all’altezza della collina e caratterizzata dal fatto che si presenti o no distacco della
vena fluida.
L’aumento di velocità dovuta alla presenza di una collina viene solitamente
descritto in letteratura utilizzando due rapporti di velocità. Se u1(z) è la velocità del
vento indisturbato sopravento e u2(x,z) è la velocità del vento in una zona in cui il
campo di moto è influenzato dalla presenza della collina, si definisce l’incremento
relativo di velocità ∆S (fractional speed-up ratio), dato da:
( ) ( ) ( )
( )zu
zuzxu
zxS
1
1,2
,
−
=∆ , (3.1)
dove z è l’altezza, misurata a partire dal suolo, e x la posizione.
Oltre all’incremento relativo di velocità ∆S si definisce anche la velocità
normalizzata S(x,z)=u2(x,z)/u1(z) (normalized speed), S è allora tale che:
1),(),( +∆= zxSzxS . (3.2)

68. 58
Figura 3-1 – Accelerazione locale sulla sommità di una collina.
In figura 3-1 compaiono H e L, due lunghezze utilizzate per descrivere la
geometria di una collina dalla forma semplificata.
H altezza della collina (rispetto alla zona circostante).
L semi-ampiezza misurata a metà altezza (H/2). L viene riferita alla direzione di
provenienza del vento.
Per una collina di larghezza indefinita, di geometria semplice come quella
rappresentata in figura 3-1, Hunt [6] nel 1980 propose la relazione (3.3) per
determinare il ∆S massimo. Il valore massimo di ∆S si osserva sulla verticale della
cima ad una quota .
L
H
S 2≅∆ , (3.3)
Per una collina a doppia simmetria, le cui linee di livello sono approssimabili a
delle ellissi, Taylor e Lee [6] nel 1984 suggerirono un diverso coefficiente di
proporzionalità, formula (3.4):
L
H
S 6,1≅∆ , (3.4)
Essendo la semi-ampiezza L misurata lungo la direzione di provenienza del vento,
a parità di H si ottiene il ∆S maggiore quando L è minimo; per valori troppo elevati
del rapporto H/L si osserva però il distacco della vena fluida e le formule (3.3) e
(3.4) non sono più attendibili anche se continuano a fornire un’idea, almeno
sull’ordine di grandezza del ∆S massimo.
Per rendersi conto dei valori che ∆S massimo può assumere si consideri una
collina avente altezza H=100 m ed L=250 m, questa porta ad incrementi di velocità
∆S massimo variabili da 0,6 a 1.

69. 59
Un alto valore di ∆S è chiaramente indice favorevole per il posizionamento
ottimale di generatori eolici. Sebbene le formule (3.3) e (3.4) siano molto
semplificate, e quindi non precise, esse danno sicuramente un’idea dell’ordine di
grandezza delle accelerazioni che possono instaurarsi nei flussi al di sopra delle
colline.
Una valutazione più precisa del ∆S prodotto su un territorio dall’orografia
complessa si può ottenere mediante una simulazione numerica accurata del sito o
mediante una serie di misurazioni effettuate direttamente sul territorio di interesse.
Una terza via è quella di studiare, in galleria del vento, il flusso dello strato limite su
un plastico del sito.
Nell’articolo [7] è riportato un confronto tra le teorie di Hunt, estese da Taylor e
Lee, a cui si riferiscono le formule (3.3) e (3.4), con i dati ottenuti da prove
sperimentali sulla collina di Askervein, nel 1982 e nel 1983, presentati nel paragrafo
successivo.
3.2 Il progetto Askervein (The Askervein Hill Project).
Molti dei recenti studi relativi all’influenza dei terreni collinari sul vento sono
stati sviluppati prendendo come riferimento i dati sperimentali raccolti presso la
collina di Askervein (57°N,7°W), nelle isole Ebridi, Scozia. Sulla collina di
Askervein si sono effettuate due campagne di misurazioni, la prima nel periodo
settembre/ottobre 1982, la seconda nel periodo settembre/ottobre 1983.
Le due campagne di misurazioni sulla collina di Askervein sono frutto di una
cooperazione internazionale tra diversi gruppi di ricerca. I gruppi che hanno preso
parte alle attività sono stati l’Atmospheric Environment Service (AES), Canada, il
Risø National Laboratory, Danimarca, l’Università di Hannover, Germania,
l’Università di Canterbury, Nuova Zelanda, ed infine il Building Research
Establishment e la ERA Technology Ltd. entrambi con sede nel Regno Unito.
In figura 3-2 è rappresentata una mappa cartografica comprendente l’area delle
misurazioni.

70. 60
Figura 3-2 – Mappa della zona presso la collina di Askervein, i punti di riferimento sono RS
(Reference Site), (74300, 20980), CP (Center Point) (75678, 23465) e HT (Hill Top) (75383, 23737).
La collina di Askervein è alta circa 116m rispetto al territorio circostante
(H=116m, 124m s.l.m), la sua semi ampiezza L, quando il vento arriva da SW, può
essere considerata pari a 250m.
La collina di Askervein è formata da curve di livello quasi ellittiche, per questo la
collina si può considerare a doppia simmetria, con piani di simmetria passanti per il
punto CP (Center Point), vedi figura 3-3. La pendenza della collina è circa 0,2 sul
versante che guarda a SW.
Il sito in studio è stato scelto tra vari disponibili considerando numerosi fattori, ma
principalmente per la sua la topografia, dato che la collina ha una geometria piuttosto
semplice e si trova all’interno di un territorio pianeggiante, se si escludono delle
colline poste a N-E e visibili in figura 3-2. Il secondo motivo che ha portato alla

71. 61
scelta del territorio sono le condizioni del vento, piuttosto regolare in intensità e
direzione di provenienza in certi periodi dell’anno.
La direzione di provenienza del vento presso la collina di Askervein, nel periodo
settembre/ottobre da S-W, fa in modo che si possano ritenere ininfluenti sul campo di
moto le colline poste a N-E della collina. La geometria semplice del sito è un
ulteriore aspetto positivo che la rende adatta a simulazioni numeriche e a studi su
plastici in galleria del vento. Le condizioni del vento dei vari siti candidati sono state
studiate monitorando i dati meteorologici a disposizione di diverse località. Per la
collina di Askervein si sono considerati come riferimento i dati anemometrici
dell’aeroporto di Benbecula.
Figura 3-3 – Postazioni anemometriche lungo le sezioni A e AA. Il vento è proveniente da una
direzione di 210° misurati in senso orario da Nord, la direzione di provenienza del vento è la stessa
considerata per le simulazioni.

72. 62
La cima della collina, denominata HT (Hill Top), giace sull’asse maggiore (linea
B) ad una distanza di circa 400m da CP. Gli anemometri sono stati posti a diverse
altezze, lungo delle direzioni significative quali la sezione AA passante per CP e
comprendente l’asse minore, la sezione A, passante per HT e parallela alla linea AA,
ed infine la sezione B comprendente i punti HT e CP. In figura 3-3 sono visibili le
sezioni A, AA e B ed il posizionamento delle torri anemometriche lungo A e AA. In
figura 3-4 sono invece rappresentati due sezioni verticali della collina,
rispettivamente lungo le linee A e AA.
Figura 3-4 – Spaccati trasversali della collina di Askervein, linea A e AA, fonte [6].
Per le misurazioni sono state dislocate torri di varie altezze equipaggiate con
strumenti anemometrici per la misura di velocità media, direzione e turbolenza.
Sono state impiegate due torri da 50m poste in RS e HT, una torre da 30m, una da
16m ed una da 17m. Quindici torri alte 10m, equipaggiate con anemometri Gill
UVW, e altre trentacinque alte 10m dotate di anemometri a coppe, sono state
dislocate lungo A, AA e B, sia nelle misure del 1982 che in quelle del 1983.
L’anemometro Gill UVW, prodotto dalla NovaLinx Corporation, di cui si può vedere
una foto in figura 3-5, consiste di tre anemometri ad elica fissati su tre assi
ortogonali, in tale maniera ogni elica è sensibile ad una componente del vento.
I dati rilevati sono denominati, nei vari lavori scientifici nei quali vengono
riportati, con le sigle MF (mean flow) e TU (turbulence) insieme ad un numero che
indica la data di acquisizione. Oltre alle misurazioni effettuate con le postazioni fisse
furono eseguiti anche alcuni sondaggi con dei TALA (Tethered Aerodynamic Lifting
Anemometer) per valutare il profilo del vento fino a 500m di quota. Queste ultime
misurazioni sono indicate con sigle analoghe a quelle relative alle altre misurazioni
ma identificate dalla sigla KT.

73. 63
In questo lavoro, per verificare le simulazioni numeriche, nel caso bidimensionale
si è fatto riferimento ai risultati sperimentali riportati nelle figure 3.4 e 3.5 di [5]
mentre, nel tridimensionale, si sono considerate le figure 10a, 10b e 11 di [11].
Figura 3-5 – Anemometro Gill UVW prodotto dalla NovaLynx Corporation.

74. 64
3.3 Costruzione della geometria bidimensionale.
Per svolgere delle simulazioni numeriche bidimensionali su colline dalla
geometria relativamente semplice come quella di figura 3-4 si può utilizzare
l’espressione seguente per descrivere il profilo della collina:
2
1
)(






+
=
L
x
H
xz . (3.5)
La formula (3.5) è stata utilizzata sia in [8] che in [2] nel caso di colline con
rapporto H/L pari a 0,4. L’equazione (3.5) per H=116m e L=250m, valori associati
ad Askervein lungo la direzione SW-NE, produce un profilo della collina come in
figura 3-6.
Figura 3-6 – Sezione della collina prodotta con l’equazione (3.5), H 116m e L 250m.
Durante le campagne di misurazioni di Askervein si è rilevata un’altezza
caratteristica di 4 m circa, come riportato in figura 3-7; che corrisponde alla
altezza, al di sopra di HT, per la quale si è osservato il valore massimo di ∆S.
In figura 3-7 è riportato il profilo di velocità misurato in due postazioni differenti
RS (Reference Site) e HT (Hill Top). Dai punti sperimentali ricavati alla stazione di
riferimento RS è possibile, tramite interpolazione, ricavare la velocità d’attrito u* e
la lunghezza di rugosità z0 che risultano pari, rispettivamente, a 0,65 m/s ed a 0,03m.
Le simulazioni 2D sulla collina di Askervein sono allora state eseguite con tali valori
di u* e z0.
In figura 3-8 è invece riportato l’andamento dell’incremento relativo di velocità
∆S in funzione della distanza dalla collina, valutato a 10 m di quota.

75. 65
y = 0,03e0,6386x
R2
= 0,9751
0,01
0,1
1
10
100
1000
0 2 4 6 8 10 12 14 16 18
velocità orizzontale u [m/s]
quotaz[m]
punti sperimentali RS
linea Fig. 3.5 [5]
punti sperimentali HT
Espo. (punti sperimentali RS)
Figura 3-7 – Profili di velocità misurati simultaneamente in RS e HT. Il grafico è una riproduzione
della figura 3.5 di [5].
-1
-0,8
-0,6
-0,4
-0,2
0
0,2
0,4
0,6
0,8
1
-1000 -500 0 500 1000
Distanza dalla sommità della collina [m]
Incrementorelativodellavelocità∆∆∆∆S
punti sperimentali
risultati WAsP [5]
Figura 3-8 – Incremento relativo di velocità in funzione della distanza dalla collina valutato alla
quota di 10m. Il grafico è una riproduzione di figura 3.4 di [5].

76. 66
3.4 Le simulazioni 2D sulla collina di Askervein.
3.4.1 Geometria e griglia.
Per riprodurre la topografia del terreno presso la collina di Askervein si è scelto di
utilizzare un profilo del terreno semplificato, dato dalla equazione (3.5). La griglia
mediante la quale si è suddiviso il dominio di calcolo è rappresentata nella figura 3-9
(in alto), nella quale è anche raffigurato un particolare della zona di ingresso (in
basso). L’altezza del dominio di calcolo è di 1 km alla quale si è ipotizzato che il
vento raggiungesse la condizione di vento geostrofico. Il dominio è inoltre lungo 7
km, con la collina posta a 1500 m dall’ingresso. Il terreno è stato suddiviso in
intervalli di lunghezza 20 m, mentre l’altezza totale del dominio è stata suddivisa in
60 intervalli di cui il primo, quello adiacente il terreno, alto 0,1 m. In totale la griglia
costruita consta di 21060 celle. La griglia è di tipo map con celle quadrangolari, ed è
stata creata col programma GAMBIT, sempre della Fluent Inc..

77. 67
7 km - 351 ∆x
1,5 km
h 0,1m
20 m
1 km
60 ∆y
particolare
altezza prima cella
Totale celle 60 x 351 = 21 060 celle
Figura 3-9 – Schema della griglia completa, sopra, e particolare dell’ingresso, sotto.
3.4.2 Condizioni al contorno.
Ingresso – Velocity Inlet
Per il profilo di velocità in ingresso si è considerata valida la legge logaritmica
(3.7) assegnando alla lunghezza di rugosità z0 un valore di 0,03 m e considerando per
la velocità d’attrito u* il valore di 0,65 m/s.
La temperatura in ingresso varia linearmente con l’altezza, partendo da un valore
di 288,15 K al suolo e diminuendo con la quota con un gradiente verticale adiabatico
di 0,976 K/100m.
Gradiente adiabatico secco Γad=-g/cp
m
K
ad
100
976,0−=Γ
zTT ad ⋅Γ+= 0 (3.6)

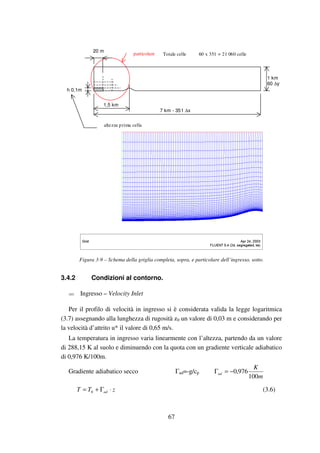
78. 68
Il valore dell’energia cinetica turbolenta k è invece ricavato da misure
meteorologiche. Facendo riferimento a [10] si vede che Panofsky e Dutton (1984)
studiarono lo strato limite atmosferico concludendo che a circa 10m di quota è valida
la seguente relazione:
48,5
*2
≈
u
k
Panofsky e Dutton (1984)
Misure effettuate ad Askervein durante le misurazioni del 1982/83 determinarono
dei valori di 4,52,4*2
÷≈uk a 10 m di quota. Il valore di k assegnato in ingresso
nelle simulazioni svolte è stato impostato pari a 5,77 u*2
per rimanere in accordo con
[8] e con [2] anche se bisogna notare che sarebbe più verosimile un valore
dell’energia cinetica turbolenta k decrescente con la quota piuttosto che uno che si
mantiene costante. Si osservi a proposito la figura 3 di [10] e le misurazioni degli
sforzi di Reynolds riportati in [12] nella figura 3.3.
Il profilo in ingresso della velocità di dissipazione dell’energia cinetica turbolenta
TDR (Turbulence Dissipation Rate) viene infine stimato con la relazione (3.9).
z
u
z
u
z
w
332/3
*
5,2
*1)/(
⋅≈=
⋅
=
κκ
ρτ
ε in accordo con [8].






=
0
ln
*
z
zu
u
κ
(3.7)
2
*77,5 uk ⋅= (3.8)
z
u 3
*
5,2 ⋅=ε (3.9)
Geostrofico – Velocity Inlet e/o Symmetry
Per il segmento denominato Geostrofico, che chiude a 1000m di quota il
dominio di calcolo si possono scegliere due opzioni come condizione al
contorno, una è la condizione velocity inlet e l’altra è la symmetry. Tra i
risultati prodotti dalle due condizioni al contorno non si riscontra una grossa
differenza, come già osservato nel capitolo precedente, anche se la condizione
symmetry sembra più corretta per trattare uno strato limite.
Terreno – Wall
La condizione al contorno del bordo di confine “terreno” è impostata come
Wall. Per un contorno di tipo Wall bisogna impostare in FLUENT la

79. 69
temperatura ed i parametri di rugosità RH (Roughness Height) e RC
(Roughness Constant), questi sono riassunti in tabella 3-1.
I valori di primo tentativo per RH e RC sono stati 0,05m e 5,886 il primo
scelto in maniera tale che RH risultasse metà della prima cella h ed RC
calcolato di conseguenza secondo l’equazione (2.31).
Uscita – Outflow
La condizione al contorno dell’uscita è stata considerata come Outflow e
non necessita, come quella symmetry, della definizione di parametri ulteriori.
Tutte le condizioni al contorno utilizzate sono riassunte in tabella 3-1.
Condizioni al contorno per simulazioni 2D su Askervein. (z0 0,03 m e u* 0,65 m/s)
Ingresso – Velocity Inlet Geostrofico – Velocity Inlet Terreno – Wall
Vx [m/s] Profio (3.7) Vx [m/s] 16,117 T [K] 288,15
Vy [m/s] 0 Vy [m/s] 0 RH [m] 0,05
T [K] Profilo (3.6) T [K] 278,387 RC 5,886
TKE [m2
/s2
] 2,438 TKE [m2
/s2
] 2,438
TDR [m2
/s3
] Profilo (3.9) TDR [m2
/s3
] 6,866E-04
Uscita – Outflow
Tabella 3-1 – Tabella riassuntiva delle condizioni al contorno per la prima simulazione effettuata,
con Geostrofico Velocity Inlet e valori dei parametri di rugosità RH=0,05m e RC=5,886.
3.4.3 Condizioni operative.
Accelerazione di gravità g: 9,8066 m/s2
Pressione operativa: 101325 Pa
Posizione del punto al quale assegnare la pressione operativa: x=0m; y=0m
Temperatura operativa: 278,39 K
Densità operativa: 1,1239 kg/m3
Per la temperatura e la densità operativa sono stati scelti i valori relativi a 1000m
di quota per un’atmosfera adiabatica con temperatura al suolo di 288,15 K.

80. 70
3.4.4 Scelta delle costanti caratteristiche del modello di turbolenza
standard k-εεεε.
Il modello di turbolenza utilizzato per la simulazione sulla collina di Askervein è
lo standard k-ε. Per la valutazione del flusso in prossimità delle pareti si sono
utilizzate le standard wall functions. Le costanti del modello vengono modificate in
base a delle relazioni che devono essere soddisfatte in condizioni di equilibrio. Dalla
relazione:
77,5
1
*2
≈=
µCu
k
(3.10)
segue Cµ=0,03.
In condizioni di equilibrio è inoltre valida la relazione (3.11):
( ) µ
ε
κ
σ
CCC ⋅−
=
12
. (3.11)
Mantenendo per C1 e σε i valori di default, è stata modificata la costante C2
secondo la (3.11). In tabella 3-2 sono riportati sia i valori di default che quelli
modificati delle costanti del modello di turbolenza k-ε standard.
Costanti del modello standard k-ε
Valori di default:
Cµ C1 C2 σκ σε Prt
0,09 1,44 1,92 1 1,3 0,85
Valori modificati:
Cµ C1 C2 σκ σε Prt
0,03 1,44 2,223 1 1,3 0,85
Tabella 3-2 – Costanti del modello k-ε standard con attivata l'equazione dell'energia (compare Prt).
3.4.5 Risultati numerici.
Nella costruzione della griglia è rilevante l’altezza h delle celle adiacenti al
terreno. Mentre per le simulazioni su terreno pianeggiante è stato possibile effettuare
delle simulazioni con h di 0,002m, nel caso del flusso sopra terreno collinare griglie
con valori così bassi di h hanno causato problemi di convergenza. Di conseguenza si
riportano solo i risultati relativi a domini discretizzati con altezza della prima cella h
pari a 0,1m.

81. 71
z0=0,03m u*=0,65m/s
parametri di rugosità:
RH=0,05m RC=5,886
0,01
0,1
1
10
100
1000
0 2 4 6 8 10 12 14 16 18 20
velocità orizzontale u [m/s]
quotaz[m]
ingresso CFD
collina CFD
ingresso (punti sperimentali)
collina (punti sperimenatli)
Figura 3-10 – Profili di velocità del vento su RS (Reference Site) ed in cima alla collina HT (Hill
Top), ottenuti con la simulazione con Geostrofico a 1 km di quota. Il cattivo andamento del vento
sulla collina è probabilmente attribuibile ai valori assegnati ai parametri di rugosità RH e RC.
z0=0,03m u*=0,65m/s
parametri di rugosità:
RH=0,05m RC=5,886
-1
-0,8
-0,6
-0,4
-0,2
0
0,2
0,4
0,6
0,8
1
-1000 -800 -600 -400 -200 0 200 400 600 800 1000
Distanza dalla sommità della collina [m]
Incrementorelativodivelocità∆∆∆∆S
CFD
risultati WAsP
punti sperimentali
Figura 3-11 – Incremento relativo della velocità ∆S a 10 m di quota, punti sperimentali e risultati
WAsP come fig. 3.4 di [5].

82. 72
z0=0,03m u*=0,65m/s
parametri di rugosità:
RH=0,03m RC=0,5
0,01
0,1
1
10
100
1000
0 2 4 6 8 10 12 14 16 18 20
velocità orizzontale u [m/s] nelle celle
quotaz[m]
ingresso CFD
collina CFD
ingresso (punti sperimentali RS)
collina (punti sperimentali HT)
Figura 3-12 – Profili di velocità in ingresso e sulla collina per h=0,1m, RH=0,03m e RC=0,5.
z0=0,03m u*=0,65m/s
parametri di rugosità:
RH=0,03m RC=0,5
-0,6
-0,4
-0,2
0
0,2
0,4
0,6
0,8
1
-1000 -800 -600 -400 -200 0 200 400 600 800 1000
Distanza dalla sommità della collina [m]
Incrementorelativodivelocità∆∆∆∆S
punti sperimentali
risultati WAsP
CFD
Figura 3-13 – ∆S a 10m di quota. Punti sperimentali e risultati WAsP ottenuti da figura 3.4 di [5].
h 0,1m, RH=0,03m e RC=0,5

83. 73
In figura 3-10 e 3-11 sono riportati i risultati numerici relativi alla simulazione
effettuata con i parametri di rugosità RH e RC di primo tentativo pari rispettivamente
a 0,05m e 5,886. Si nota come i valori calcolati si discostino da quelli rilevati
sperimentalmente, specialmente per quanto concerne la zona sottovento rispetto alla
collina, la zona occupata dalla scia visibile in figura 3-11.
Si sono eseguite allora altre simulazioni su superfici piane, come quelle descritte
nel capitolo 2, nelle quali si sono progressivamente diminuiti i valori assegnati ad i
parametri di rugosità RH e RC osservando come si ottenessero dei profili in uscita
dal dominio sempre più vicini alla legge logaritmica e, con gli stessi coefficienti, per
le simulazioni per la collina dei risultati più vicini ai punti sperimentali.
I valori di RH=0,03m e RC=0,5 si sono considerati accettabili sia per le
simulazioni su terreni piani che per le simulazioni sulla collina di larghezza
indefinita, i risultati per questi ultimi valori dei parametri di rugosità sono quelli delle
figure 3-12 e 3-13.
Dal confronto delle figure 3-10 e 3-11 con le corrispondenti 3-12 e 3-13 si evince
come siano migliorati i risultati delle simulazioni tramite la regolazione dei parametri
di rugosità RH e RC, le velocità previste dalle ultime simulazioni svolte, quelle delle
figure 3-12 e 3-13, infatti sono più vicine ai punti sperimentali di riferimento.
Come valore indicativo da assumere per i parametri di rugosità si consiglia allora
di assegnare, quando si discretezza il dominio con h=0,1m, ad RH il valore della
lunghezza di rugosità z0, in questo caso 0,03m, ed a RC 0,5, il valore impostato
inizialmente in FLUENT.
.

84. Capitolo 4 Simulazioni 3D sulla collina di Askervein.
4.1 Geometria. Costruzione del dominio di calcolo.
Grazie alla disponibilità del Dr. P. Taylor dell’Università di York (Canada) e dei
suoi collaboratori Mr. W. Weng e Mr. J. Walmsey, si è entrati in possesso di due
mappe digitalizzate dell’area in studio, comprendente la collina di Askervein.
Una delle due mappe è un quadrato di lato 6 km che comprende la sola collina di
Askervein mentre, il secondo file descrive una area quadrata di lato 16 km, e quindi
riporta sia la collina in studio, sia alcune colline che si trovano a N-E rispetto ad
essa..
Entrambi i files citati sono matrici di 256x256 quote z, per cui il primo,
comprendente l’area di dimensioni minori, ha una risoluzione maggiore, il secondo,
che comprende una area maggiore.
In figura 4-1 sono visualizzati gli elaborati grafici relativi alle due mappe, nei
quali sono visibili le curve di livello.

85. 75
10
10
10
10
10
10
10
20
20
20 20
20
20
30
30
30
30
30
40
40
40
40
40
50
60
50
50
50
60 60
60
70
70
70
80
80
80
90
9090
100
100
100 110
120
130 140
140
Ovest - Est
Sud-Nord
-2500 0 2500 5000
-4000
-2000
0
2000
4000
Frame 001  08 Apr 2003 Frame 001  08 Apr 2003 
10
10
10
10
10
10
20
20
20
30
30
405060
7080
90
100
120
120
Ovest - Est
Sud-Nord
-3000 -2000 -1000 0 1000 2000 3000
-3000
-2000
-1000
0
1000
2000
3000
Frame 001  08 Apr 2003 Frame 001  08 Apr 2003 
Figura 4-1 – Mappe digitalizzate della zona presso la collina di Askervein elaborati col programma
Tecplot. In alto si vede un ingrandimento della mappa quadrata con lato 16km; in basso è
rappresentata l’intera mappa di lato 6km.

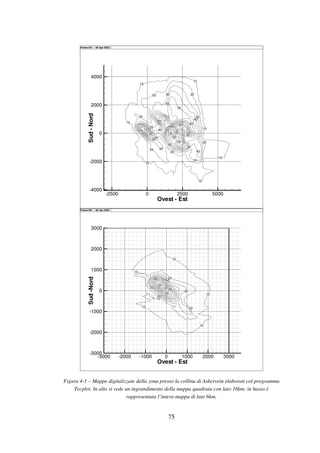
86. 76
Le due mappe disponibili sono state inizialmente convertite dal formato .grd,
leggibile col programma di rappresentazione di dati Surfer, al formato .dat che
invece può essere letto dal programma di elaborazione e visualizzazione Tecplot.
Delle due mappe si è usata quella con lato 6km, con la sola collina di Askervein.
Col programma Tecplot tramite una procedura descritta in [2] si è creata una
matrice rettangolare 80x80 compresa negli intervalli ∆x=-1700m÷3900m e ∆y=-
2200m÷4500m. La matrice creata, detta zona 001, e la zona rettangolare di partenza
sono rappresentate in figura 4-2.
V1
V2
-3000 -2000 -1000 0 1000 2000 3000 4000 5000
-3000
-2000
-1000
0
1000
2000
3000
4000
Frame 001  10 Apr 2003 Frame 001  10 Apr 2003 
Figura 4-2 – Mappa digitalizzate .dat in rosso e zona rettangolare 80x80 in verde.
Bisogna notare che la scelta di utilizzare una matrice 80x80 è stata dettata dal
fatto che tale matrice è stata creata, per essere poi gestita dal generatore di griglia
Gambit che, per creare la superficie del terreno come interpolazione di punti,
permette al massimo tali dimensioni.
Una matrice 80x80 in un rettangolo spaziale di 5,8km x 6,7km comporta una
distanza di 72,5m e 83,75m tra i punti della matrice, nelle due direzioni ortogonali

87. 77
Uno degli aspetti da sviluppare in futuro sarà quello di incrementare la risoluzione
utilizzata per rappresentare il suolo.
La superficie del terreno, basata su una matrice originale di punti che non una
griglia bidimensionale, viene quindi proiettata, mediante una procedura di
interpolazione permessa da Tecplot, dalla zona 001 alla nuova zona rettangolare.
Ambe le zone citate, la zona 001 e quella rettangolare creata, sono visualizzate in
figura 4-2.
Il risultato di tale procedura è un file ASCII, al quale è assegnata l’estensione
.dat nel quale sono riportate le coordinate cartesiane (x,y) dei punti che
costituiscono la zona rettangolare e la rispettiva quota z.
Tale file è importabile e manipolabile direttamente col programma Gambit
attraverso il comando di importazione vertici.
Il risultato della procedura sopra descritta è visibile in figura 4-3 dove è riportato
il profilo della collina di Askervein vista da Nord-Est, con la scala delle altezze
amplificata rispetto agli assi x , y.
0
50
100quotaz[m]
-3000
-2000
-1000
0
1000
2000
3000
4000
Est-Ovest
-3000
-2000
-1000
0
1000
2000
3000
4000
Sud-Nord
X Y
Z
117.266
109.695
102.124
94.5527
86.9817
79.4106
71.8396
64.2685
56.6974
49.1264
41.5553
33.9842
26.4132
18.8421
11.2711
Frame 001  18 Mar 2003 Frame 001  18 Mar 2003 
Figura 4-3 – Vista prospettica da Nord-Est della zona rettangolare in seguito all’interpolazione
inversa con la zona iniziale 001.

88. 78
La matrice 80x80 di vertici così costruita è stata quindi importata all’interno di un
file di Gambit attraverso il comando di importazione vertici, ed è stata generata
mediante una procedura di interpolazione di vertici la superficie che andava a
costituire il terreno, il confine inferiore del dominio di calcolo.
In figura 4-4 si vede, in alto, la matrice 80x80 di vertici importati all’interno di un
file .dbs di Gambit, in basso è invece rappresentata la superficie interpolante tali
vertici.
Al fine di costruire il dominio di calcolo, dovendo studiare una condizione di
vento proveniente da direzione di 210° misurati in senso orario da Nord, si è
disegnato un volume di calcolo, delimitato superiormente da un rettangolo a 1000m
di quota e inferiormente dalla superficie del terreno, precedentemente creata, le altre
facce di confine sono state invece create mediante piani verticali, rispettivamente
parallele e normali alla direzione di provenienza del vento, come rappresentato in
figura 4-5.

89. 79
Figura 4-4 – Vertici importati in GAMBIT e superficie interpolante.

90. 80
Figura 4-5 – Costruzione del dominio di calcolo, ottenuto sezionando un parallelepipedo con la
superficie del terreno. Per poter successivamente assegnare i profili in ingresso in FLUENT il
volume di controllo è stato ruotato e traslato fino a portare le facce del dominio paralleli agli assi x e
y.
In figura 4-6 è invece rappresentata la condizione del vento studiata.

91. 81
Figura 4-6 – Posizionamento anemometri e direzione del vento per dati di fig. 10 di [11].
Il volume così ottenuto col programma Gambit è stato infine traslato e ruotato
fino a portare le facce del dominio di calcolo coincidenti con gli assi x e y, tale
accorgimento risulta particolarmente utile quando si devono assegnare le condizioni
al contorno sotto forma di profili.
4.2 Griglia.
La geometria che costituisce il dominio di calcolo, costruita come descritto nel
paragrafo precedente, è stata discretizzata in una griglia strutturata a volumi
esaedrici. Innanzitutto si sono discretizzate le facce del dominio. Quella inferiore,
cioè la superficie del terreno, è stata suddivisa con una griglia al elementi
quadrangolari di tipo map, con distanze medie di 30m tra due punti successivi in
entrambe le direzioni.
Le facce laterali del dominio che dal terreno vanno al geostrofico (1000m) sono
state discretizzate con una griglia caratterizzata da celle le cui dimensioni verticali
crescono all’aumentare della quota, con la prima cella alta 0,6m e un totale di 50
celle. Una volta proceduto con la discretizzazione delle sei facce che delimitano il
volume, questo è stato infine discretizzato con una griglia di tipo map, quindi con
volumetti esaedrici, per un totale di un milione di celle.

92. 82
Con le risorse di calcolo a disposizione non ci si può spingere ad un numero
maggiore di celle dal momento che durante le elaborazioni numeriche si è visto che
venivano utilizzati circa 680 Mbyte di memoria RAM su 750 Mbyte circa
disponibili.
In figura 4-7 è rappresentato il dominio di calcolo discretizzato più un particolare
in prossimità del terreno.
30 m
30 m
h 0,6 m
3 km
6 km
1 km
Totale celle:
100 x 200 x 50 = 1 000 000
particolare
Figura 4-7 – Schema del dominio di calcolo discretizzato e particolare all’intersezione di terreno,
lato destro e uscita.

93. 83
La fase di preparazione del dominio di calcolo comporta anche la possibilità di
assegnare le condizioni al contorno, l’ingresso è stato impostato come velocity-inlet,
il terreno come wall, le facce destra, sinistra e superiore, detta geostrofico, come
symmetry, mentre l’uscita è fissata come outflow.
4.3 Impostazioni delle simulazioni.
Per le simulazioni tridimensionali sono state usate le stesse impostazioni delle
simulazioni bidimensionali descritte nel capitolo precedente, per cui il valore dell
altezza di rugosità, RH, è stato impostato pari a 0,03m, ovvero uguale alla lunghezza
di rugosità z0, e la costante di rugosità, RC, a 0,5, valore pre-impostato nel codice
Fluent.
Sono state effettuate quattro simulazioni, due col modello di turbolenza k-ε
standard e due col modello RNG k-ε. Per ciascun modello di turbolenza è stata
sviluppata una prima simulazione con le standard wall-functions, ed una seconda con
le non-equilibrium wall-functions per la discretizzazione dell’interazione tra fluido e
terreno.
I risultati numerici sono stati confrontati tra loro e con i risultati presenti in
letteratura; e in particolare, per verificare la bontà delle elaborazioni, si sono
considerati i risultati rappresentati nei grafici 10a, 10b e 11 di [11].
4.4 Elaborazione grafica dei risultati.
Per poter rappresentare i risultati delle simulazioni e confrontarli con quelli
rappresentati nei grafici 10a, 10b e 11 di [11], è stato necessario costruire delle curve
a 10m di quota dirette come la linea B, A e AA, rappresentate in figura 4-8. La
procedura seguita per costruire tali linee ed i grafici seguenti è descritta in Appendice
III.

94. 84
Figura 4-8 – Alcune facce discretizzate: “terreno” in nero, “sinistra” in blu e “uscita” in rosso.
Sono visibili inoltre le curve a 10m di quota A, AA e B colorate in rosso.
Oltre alle linee A, B e AA sono state definite nel codice Fluent le funzioni
“distanza da HT”, “distanza da CP” e velocità orizzontale Vh, modulo della
componente orizzontale del vettore velocità.
α
Figura 4-9 – Linee A, AA e B. funzioni “distanza da CP” e “distanza da HT”.

95. 85
In seguito alla roto-traslazione del dominio di calcolo, nel nuovo sistema di
coordinate, prendendo come riferimento la figura 4-9, risulta:
Coordinate di HT:
XHT 717,751m
YHT 1547,444m
Coordinate di CP:
XCP 1109,229m
YCP 1459,385m
Equazione retta A: Y=ma X+qa
ma=4,446; qa=-1643,413m
Equazione retta AA: Y=maa X+qaa
maa=ma=4,446; qaa=-3471,837m
distanza da HT:
a
HT
HT
XX
d
αcos
−
= (4.1)
distanza da CP:
a
CP
CP
XX
d
αcos
−
= (4.2)
)( aa marctg=α (4.3)
Velocità orizzontale media Vh:
22
VUVH += (4.4)
L’incremento relativo di velocità ∆S è stato definito considerando come velocità
di riferimento la velocità orizzontale media VH valutata a una distanza a monte di HT
e di CP pari a 1000m. Nelle figure 4-10/11 sono rappresentati i risultati relativi alle
simulazioni effettuate coi modelli di turbolenza standard e RNG, quelli ottenuti da
simulazioni effettuate da altri autori [11] e i dati sperimentali, riferiti alla sezione
AA. Nelle figure 4-12/13 sono rappresentati i risultati analoghi relativi alla sezione
A. Si evidenzia immediatamente come il codice e le impostazioni utilizzate nel
presente lavoro permettano di ottenere risultati confrontabili con quelli ottenuti in
simulazioni numeriche effettuate da altri autori. Risulta comunque la difficoltà di
prevedere il flusso a valle della collina, cioè nella zona in cui possono essere presenti
scie e distacchi di flusso. Ciò è reso visibile dal fatto che le maggiori discordanze tra
risultati numerici sperimentali si osservano nella sezione corrispondente alla parte
più alta della collina, sezione A, dove sono maggiori le pendenze del terreno.

96. 86
Figura 4-10 – fig. 10a di [11]
-1
-0,8
-0,6
-0,4
-0,2
0
0,2
0,4
0,6
0,8
1
-1000 -500 0 500 1000
distanza orizzontale da CP (linea AA) [m]
∆∆∆∆S
0
100
200
300
400
500
600
700
800
900
1000
z[m]
std. k-e; std. w-f std. k-e; n-e w-f
punti sperimentali profilo collina
Figura 4-11 – Incremento relativo di velocità lungo la sezione AA, valori a 10m di quota.
-1
-0,8
-0,6
-0,4
-0,2
0
0,2
0,4
0,6
0,8
1
-1000 -500 0 500 1000
distanza orizzontale da CP (linea AA) [m]
∆∆∆∆S
0
100
200
300
400
500
600
700
800
900
1000
z[m]
RNG k-e; std. w-f RNG k-e; n-e w-f
punti sperimentali profilo collina
Figura 4-12 – Grafico analogo a figura 4-11, risultati modello RNG.

97. 87
Figura 4-13 – fig. 10b di [11]
-1
-0,8
-0,6
-0,4
-0,2
0
0,2
0,4
0,6
0,8
1
-1000 -500 0 500 1000
distanza orizzontale da HT (linea A) [m]
∆∆∆∆S
0
100
200
300
400
500
600
700
800
900
1000
z[m]
std. k-e; std. w-f std. k-e; n-e w-f
punti sperim. profilo collina
Figura 4-14 – Incremento relativo di velocità lungo la sezione A, valori a 10m di quota.
-1
-0,8
-0,6
-0,4
-0,2
0
0,2
0,4
0,6
0,8
1
-1000 -500 0 500 1000
distanza orizzontale da HT (linea A) [m]
∆∆∆∆S
0
100
200
300
400
500
600
700
800
900
1000
z[m]
RNG k-e; std w-f RNG k-e; n-e w-f
punti sperim. profilo collina
Figura 4-15 – Grafico analogo a figura 4-14, risultati modello RNG.

98. 88
In figura 4-16a e 4-16b è rappresentato l’incremento relativo di valutato su una
linea verticale che parte dalla cima della collina. L’incremento relativo di velocità è
stimato prendendo come velocità di riferimento la velocità calcolata con la legge
logaritmica (u*=0,654 m/s; z0=0,03m come in [10]).
a)
1
10
100
-0,5 0 0,5 1 1,5
∆∆∆∆S sulla cima della collina (punto HT - hill top )
quotaz[m]
std. k-e; std. w-f
std. k-e; non-eq. w-f
punti sperimentali
b)
1
10
100
-0,5 0 0,5 1 1,5
∆∆∆∆S sulla cima della collina (punto HT - hill top )
quotaz[m]
RNG k-e; std w-f
RNG k-e; non-eq. w-f
punti sperimentali
Figura 4-16 – Incremento relativo di velocità ∆S calcolato al di sopra di HT. Figura 4-16a per il
modello standard k-e e figura 4-16b per il modello RNG k-e.

99. 89
4.5 Calcolo della densità di energia.
La massima potenza estraibile dal vento è proporzionale al cubo della velocità
orizzontale; ciò vuol dire che un incremento, anche piccolo, della velocità media del
vento in particolari punti del sito in esame, può dare notevoli benefici in termini di
energia prodotta. La densità di energia eolica, relativa ad una superficie A, è data dal
prodotto dell’energia cinetica disponibile per unità di massa, moltiplicata per la
portata massica che attraversa l’area A stessa.
Nel caso in cui la superficie A sia quella interessata da un rotore eolico si deve
considerare nell’espressione della densità di energia eolica la sola componente
orizzontale del vento, essendo la superficie A un cerchio che giace su un piano
verticale.
La densità di energia eolica, che dimensionalmente è una potenza per unità di
area, è definita da:
P/A= 321 HVρ .
In figura 4-17 è raffigurato l’andamento della massima energia estraibile dal
vento.
Figura 4-17 – Densità di energia del vento [W/m2
]in funzione della velocità del vento.
È stata quindi definita in FLUENT la funzione “densità energetica”, mediante
l’espressione precedentemente scritta, che il codice permette di visualizzare alla
quota desiderata su superfici ottenute traslando la superficie del terreno.

100. 90
Nelle figure 4-18 e 4-19 sono rappresentate due mappe di densità energetica,
valutate rispettivamente a 100m e 50m di quota, relative alla simulazione effettuata
col modello di turbolenza standard k-ε e le standard wall functions per modellare
l’iterazione tra flusso e terreno.
Si può dimostrare inoltre come incremento relativo di velocità ed incremento
relativo di densità energetica (massima potenza estraibile) siano strettamente
collegati. Infatti:
incremento relativo di velocità:
0
0
V
VV
S
−
=∆ (4.5)
incremento relativo di densità di energia:
0
0
P
PP
Prel
−
=∆ (4.6)
Essendo 3
2
1
VP ⋅⋅= ρ e 3
00
2
1
VP ⋅⋅= ρ si ottiene:
( )332
+∆⋅+∆⋅∆=∆ SSSPrel (4.7)
Per esempio, ad un ∆S del 20% corrisponde un ∆Prel del 72,8%.

101. 91
Figura 4-18 – Mappa di densità energetica P [W/m2
], valutata a 100m di quota.
Figura 4-19 – Mappa di densità energetica P [W/m2
], valutata a 50m di quota.

102. 92
Conclusioni.
Nel lavoro svolto è stato utilizzato un codice di calcolo CFD di tipo commerciale
per lo studio della propagazione dello strato limite atmosferico.
Tale studio è orientato a valutare la capacità del codice suddetto, e dei modelli di
turbolenza implementati in esso, di valutare il campo di moto che si instaura al di
sopra di terreni dalla orografia complessa, al fine di individuare le postazioni più
adatte al posizionamento di generatori eolici.
Sono stati impiegati due modelli di turbolenza; il k-ε nella versione standard e
RNG.
Una serie di simulazioni bidimensionali, su terreno piano e su un profilo
semplificato di collina che riproduceva comunque una collina reale di cui si era in
possesso di dati sperimentali, sono servite a ricavare tutti i parametri (modello di
turbolenza, condizioni al contorno, parametri di rugosità del terreno, profili in
ingresso e altri) necessari ad adattare il codice a riprodurre la propagazione dello
strato limite atmosferico.
Per valutare l’attendibilità delle simulazioni sono stati impiegati come valori di
confronto i dati sperimentali disponibili in letteratura e relativi al sito in studio, e
sono stati quindi impostati nel codice i parametri necessari a riprodurre le condizioni
meteorologiche relative alle misurazioni sperimentali.
Le simulazioni tridimensionali hanno richiesto un notevole lavoro preliminare per
stabilire la procedura di costruzione e discretizzazione del dominio di calcolo e di
impostazione del codice.
Le risorse di calcolo disponibili hanno permesso di discretizzare il dominio di
calcolo con un milione di celle, sufficienti comunque a studiare il territorio per il
quale si era in possesso di misure sperimentali. Il territorio studiato è vasto diciotto
chilometri quadrati e le simulazioni tridimensionali svolte hanno richiesto
mediamente un tempo di 36 ore per portare la soluzione a convergenza.
Il confronto tra risultati numerici e dati sperimentali è stato effettuato elaborando i
valori di velocità calcolati nei punti di posizionamento degli anemometri e, per far
ciò, si è sviluppata una procedura di estrapolazione ed elaborazione dei risultati
numerici.
Le prove effettuate hanno mostrato una buona corrispondenza tra risultati
sperimentali e numerici.
Gli andamenti delle velocità, su alcuni piani verticali contenenti i punti di
posizionamento degli anemometri, hanno mostrato un ottimo accordo coi risultati
sperimentali. Qualche discordanza si è osservata nella zona a valle della collina, dove
sono presenti separazioni di flusso.

103. 93
Una volta affinati i parametri della simulazione, il flusso è descritto in maniera più
accurata rispetto a codici di calcolo che si basano su correlazioni semi-empiriche.
L’errore relativo risulta circa pari al 14% per una quota compresa tra 10m e 100m.
Questa quota è ritenuta la più significativa per lo sfruttamento dell’energia eolica
perché comprendente le quote di posizionamento dei comuni anemometri e delle
turbine eoliche. Dato che in tale fascia i risultati sono fortemente influenzati dagli
effetti che il terreno ha sul flusso, ulteriori migliorie sono legate alla valutazione
corretta del profilo del vento nello strato più vicino al terreno. È inoltre necessario un
approfondimento dell’andamento dell’energia cinetica turbolenta all’interno dello
strato limite atmosferico e sulla sua giusta valutazione nel processo di calcolo
sviluppato.
Anche se le misurazioni disponibili costituiscono una vasta e accurata campagna
di rilevamenti, ulteriori raffronti con altri casi possono sicuramente portare ad un
affinamento del processo di calcolo, specialmente per territori particolarmente
irregolari per i quali il campo di moto è più complesso.
In definitiva, le simulazioni effettuate si sono mostrate sufficientemente affidabili
per stimare l’energia eolica estraibile e possono quindi essere impiegate per
valutazioni più accurate, rispetto a quelle ottenibili con altri metodi, soprattutto in
presenza di orografia complessa.

104. 94
Appendice I – Costruzione dei file contenenti i profili in
ingresso.
I file che contengono i profili possono essere costruiti con l’uso di qualunque
editor ASCII e con l’ausilio di programmi in grado di gestire delle tabelle numeriche
come fogli elettronici o software specifici per calcoli matematici e ed elaborazione di
dati.. Nel mio caso si è fatto uso del programma Mathcad e di un semplice editor
ASCII.
Le strutture di un file di tipo “profile” bidimensionale e tridimensionale sono le
seguenti, riportate nella tabella 4-1:
File bidimensionale File tridimensionale
((nome profilo point n)
(x
x1 x2 … xn)
(y
y1 y2 … yn)
(var-1
v1-1 v1-2 … v1-n)
(var-2
v2-1 v2-2 … v2-n)
...
(var-m
vm-1 vm-2 ... vm-n))
((nome profilo point n)
(x
x1 x2 … xn)
(y
y1 y2 … yn)
(z
z1 z2 … zn)
(var-1
v1-1 v1-2 … v1-n)
(var-2
v2-1 v2-2 … v2-n)
...
(var-m
vm-1 vm-2 ... vm-n))
Tabella 4-1 – Struttura dei file dei profili
Le prime due grandezze, nel caso 2D, sono le coordinate x e y degli n punti nei
quali si definiscono le m variabili. Per un profilo tridimensionale compare la
coordinata z, un profilo tridimensionale può essere costruito proiettando un profilo
bidimensionale con una procedura implementata nel programma Fluent
Se z rappresenta la quota e l’ingresso è posizionato per x=0 sono nulle tutte le x e
pure tutte le y, in questa maniera il codice Fluent comprende che il profilo
bidimensionale è stato proiettato lungo la direzione y. Bisogna stare attenti che le
coordinate presenti nel file di profilo siano le stesse della superficie alla quale si
riferiscono.

105. 95
Appendice II – Elaborazione dei file grd di terreni complessi.
Per le simulazioni su Askervein si sono costruiti dei domini di calcolo a partire da
file .grd di Surfer. Letti i file .grd con Surfer 8 sono stati salvati nel formato
ASCII XYZ (*.dat) gestibili col programma Tecplot.
Una volta avviato Tecplot si carica il file *.dat appena creato
File => Load Datafile(s).
Si costruisce una zona rettangolare:
Data => Create Zone => Rectangular
Viene interpolata la zona che contiene l’orografia con la zona rettangolare:
Data => Create Zone => Interpolate => Inverse-Distance
Dal pannello di interpolazione si seleziona come zona sorgente quella contenente i
dati topografici (001) e come zona finale la rettangolare. Sono disponibili in
Tecplot diverse tecniche di interpolazione; i valori di default danno dei buoni
risultati.
Si cancella la zona che originalmente conteneva l’orografia (001).
Data => Delete Zone
Viene salvato un file ASCII contenente i vertici costituenti la zona rettangolare
sottoforma di coordinate tabellate.
File => Write Datafile
Nel pannello di scrittura del file si seleziona ASCII, point format; per quanto
riguarda la precisione si possono selezionare 3 cifre decimali, ovvero le coordinate
dei punti vengono salvate arrotondate al millimetro.
Il file .dat creato contiene alcune righe di comandi prima dei valori tabellati
delle coordinate dei punti. Perché la matrice di vertici sia leggibile con Gambit
devono essere cancellate dal file .dat tutte le righe che contengono comandi e
lasciate le sole righe contenenti coordinate di punti.
Per poter importare con Gambit il file .dat contenente una serie di vertici, si
avvia Gambit e si lancia il comando di acquisizione vertici.
File => Import => Vertex Data
Il comando per costruire una superficie dall’interpolazione di vertici prende il
nome di Create Real Surface from Vertex Rows. Il resto della costruzione non
presenta particolari procedure.

106. 96
Si nota però che si può migliorare la risoluzione con cui si riproduce il terreno se
viene fatta ruotare in Tecplot la zona 001 in maniera da portare la direzione di
provenienza del vento diretta lungo l’asse y (o x), in questa maniera si può creare una
zona rettangolare che ricopre una area meno vasta, quella che corrisponde
esattamente alla superficie “terreno” del dominio di controllo. Chiaramente, a zone
rettangolari più piccole, create con lo stesso numero di punti, corrisponde una
risoluzione maggiore. Con tale accorgimento si riesce a crea una matrice di vertici
importabile in Gambit distanziati tra loro di 60m circa.
Il comando che in Tecplot permette di ruotare una zona è dato da:
Data => Alter => 2D rotate…

107. 97
Appendice III – Procedura seguita per i grafici di Capitolo 4.
Nelle figure 4-11 e 4-12 è rappresentato l’incremento relativo di velocità,
calcolato rispetto alla velocità orizzontale, in funzione della distanza dal punto CP, e
dal punto HT per le figure 4-14 e 4-15. Per costruire tali grafici si sono seguiti in
FLUENT una serie di passaggi. Innanzitutto si è creata la superficie alla quota di
10m ottenuta traslando di 10m il terreno.
Surface => Transform => Translate
Successivamente si sono create le superfici “linea A” e “linea AA” passanti
rispettivamente per HT e CP.
Per una generica linea a 10m di quota si ha la curva della retta qmxy += . I valori
di m e q per le linee A e AA sono riportati nel Capitolo 4. La curva A è formata da
punti appartenenti alla superficie ottenuta traslando il terreno di 10m ed i cui punti
soddisfano la qmxy += . Si allora definita una grandezza generica mxy −=φ .
Define => Custom Field Function
Dopo aver creato la funzione mxy −=φ si è costruita la linea A e AA col
comando:
Surface => Iso-Clip
Nella finestra “Clip Surface” si è selezionata la superficie posta a z 10m. Nella
cornice “Clip to values of” si è selezionata la funzione appena creata y=mx che si
trova all’interno delle funzioni definite dall’utente (Custom Field Functions).
Infine sia come valore minimo che come massimo si assegna il valore qa per la linea
A e qaa per la linea AA.
Per poter tracciare i grafici si devono ancora definire tre grandezze, la velocità
orizzontale e la distanza da HT e da CP. Tali due grandezze sono gia state definite
nel capitolo 4, ed il percorso da seguire è sempre
Define => Custom Field Function.
Per esportare una tabella numerica di valori Vh e “distanza da HT” si segue il
percorso
Plot => XY Plot
Si devono deselezionare sia il campo delle x che delle y. Nelle ascisse si seleziona
la funzione “distanza da…”, mentre per le ordinate si seleziona la velocità
orizzontale, la superficie per la quale si rappresentano tali valori è invece la linea
corrispondente alla grandezza “distanza da…” scelta. Selezionando Write si salva un
file .xy, scritto in ASCII, che contiene due colonne di valori.

108. 98
Bibliografia.
[1] L’impatto ambientale dei sistemi energetici; G. Cau D. Cocco,
SGEditoriali Padova (2002).
[2] Simulazione numerica della propagazione dello strato limite
atmosferico attraverso ostacoli dalla geometria assegnata, tesi di
laurea di S. Forma, Università degli studi di Cagliari (2002).
[3] Manuale di Fluent 5; Fluent Incorporated (1998).
[4] Manuale di Gambit 2.0; Fluent Incorporated (1998).
[5] European Wind Atlas; Risø National Laboratory, Danimarca; I. Troen
e E. Lundtang Petersen (1989).
[6] The Askervein Hill Project: overview and background data; P. A.
Taylor e H. W. Teunissen; Boundary-Layer Meteorology 39 (1987) 15-
39.
[7] The Askervein Hill Project: mean wind variations at fixed heights
above ground; J. R. Salmon, A. M. Hoff, R. Johnson, R. E. Mickle, P.
A. Taylor, G. Tetzlaff e J. L. Walmsley; Boundary-Layer Meteorology
43 (1988) 247-271.
[8] Flow over topographic configurations of interest, comparison of
results of different models; M. Esteban, A. Crespo, J. Garcia, J.
Hernandez; articolo tratto da “European Wind Energy Conference”
(2001) 729-732.
[9] The critical Reynolds number for rough-wall boundary layers; W. H.
Snyder e I. P. Castro; Journal of Wind Engineering and Industrial
Aerodynamics 90 (2002) 41-54.
[10] The Askervein Hill Project: a finite control volume prediction of
three-dimensional flows over the hill; G. D. Raithby, G. D. Stubley e
P. A. Taylor; Boundary-Layer Meteorology 39 (1987) 247-267.
[11] A mixed spectral finite-difference model for neutrally stratified
boundary-layer flow over roughness changes and topography; A.C.M.
Beljaars, J.L. Walmsley and P.A. Taylor; Boundary-Layer
Meteorology 38 (1987) 273-303.

109. 99
[12] The atmospheric boundary layer; J. R. Garrat; Cambridge
atmospheric and space science series (1992).
[13] Wind field simulations at Askervein hill; J. Leroy; relazione tecnica
per la Vector CFD Consulting(1999); reperibile al sito internet:
http://windsim.com/documentation/presentations/9910_askervein/main
.html
[14] Improved Turbulence Models for Computational Wind Engineering;
tesi di PhD di Mr. Gary Eason, Università di Nottingham (2000);
reperibile al sito internet:
http://www.nottingham.ac.uk/~evzngw/download.htm
[15] Software per la conversione dei file dxf in xyz; Guthrie CAD/GIS
software; reperibile al sito internet: www.guthcad.com.au
[16] An introduction to computational fluid dynamics; H. K. Versteeg, W.
Malalasekera; Longman (1995)
[17] Dispense del professore Mr. Chin per il corso ”CFD (Computational
Fluid Dynamics)”; University of Sheffield, (2000)