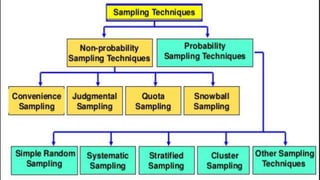
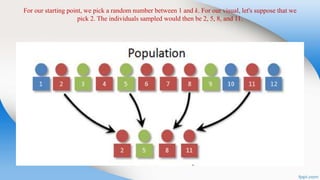
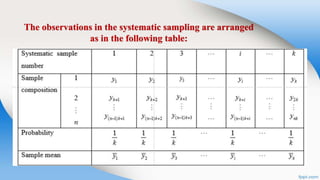
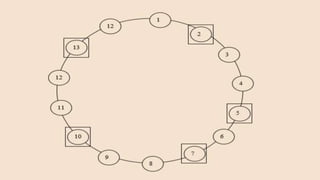
Systematic random sampling is a type of probability sampling where units from a larger population are selected according to a random starting point and a fixed periodic interval. This method is simple, convenient, and economical compared to simple random sampling. It involves randomly selecting a starting point between 1 and the sampling interval, then selecting every kth unit thereafter. While it provides unbiased estimates, it could lead to over or underrepresentation if the population has a hidden periodic pattern.

1. Systematic Random Sampling

2. WHAT IS SAMPLE, SAMPLING, TYPES OF SAMPLIG TECHINIQUES?

3. INTRODUCTION
 Sample is a group of people, objects, or items that are taken from a larger
population for measurement.
 Sampling is a statistical procedure that is concerned with the selection of the
individual observation.
 Probability sample is a sample in which every unit in the population has a
chance (greater than zero) of being selected in the sample, and this probability
can be accurately determined.
 Non-Probability sampling is any sampling method where some elements of the
population have no chance of selection (these are sometimes referred to as 'out of
coverage'/'undercovered')

5. DIFFERENT TYPES OF SAMPLING TECHINIQUES
Probability Sampling includes:
1. Simple Random Sampling,
2. Systematic
Random Sampling,
3. Stratified Sampling,
4. Cluster Sampling
5. Multistage Sampling.
Non-Probability sampling
methods include
1. convenience sampling
2. quota sampling
3. purposive sampling

6. Systematic Random Sampling
In systematic Random Sampling, the first unit is selected with
the help of random the help of random numbers and the
remaining units are selected automatically according to a
predetermined pattern. This method is known as systematic
sampling.

7.  Systematic random sampling is simple and it is widely used in
various types of surveys i.e., in census work, forest surveys, milk
yield surreys and in fisheries etc. because in many situations it
provides estimates more efficient than simple random sampling
 Systematic sampling is simple and convenient to apply. It is also
economical and required less time than simple random sampling.
But it does not give a right representation of the population

8. For our starting point, we pick a random number between 1 and k. For our visual, let's suppose that we
pick 2. The individuals sampled would then be 2, 5, 8, and 11.

10. Suppose the N units in the population are numbered 1 to N in some
order. Suppose further that N is expressible as a product of two integers
n and k, so that . N= nk
To draw a sample of size n,
 Select a random number between 1 and k.
 Suppose it is i. - Select the first unit whose serial number is i.
 Select every th k unit after th i unit.
 Sample will contain , ,1 2 ,..., ( 1) i i k k i n k + + + − serial number
units.

11. So first unit is selected at random and other units are selected systematically.
This systematic sample is called kth systematic sample and k is termed as
sampling interval. This is also known as linear systematic sampling.

12. The observations in the systematic sampling are arranged
as in the following table:

13. Linear systematic sampling is a systematic sampling method
where samples aren't repeated at the end and 'n' units are selected to be a part of
a sample having 'N' population units. Rather than selecting these 'n' units of
a sample randomly, a researcher can apply a skip logic to select these.

14. Circular Systematic Sampling a random start between 0 and N (including N)
is selected and every kth unit from that is selected. If r>n, then before n sample
units are selected, r+ik would be greater than N. In such a case, the units with
serial numbers 1, 2, ... are appended at the end of the list and selection is
continued till n units are selected.

15. a) Liner Systematic sampling(LSS)
CASE-1(N= nk)
Let a random number r from 1 to K be selected. The selected
random number r is known as the random start and K is called
the sampling interval. In this procedure, the sample comprise the
units r, r+k, r+2k,………,r+(n-1)k. The technique will generate
systematic samples of size n with equal probability.

16. CASE-2(N ≠ nk)
In this case, the present sampling scheme will give rise to samples of
unequal size. The sampling interval “k” is taken as an integer nearest to
N/n; a random number chosen from 1 to k and every kth unit is drawn in
the sample. Under this condition, the sample size is not necessarily ‘n’ and
some cases it may (n-1)

17. Circular Systematic Sampling
The disadvantages of liner systematic sampling(LSS) regarding the actual
sample size being different from that required and the sample mean being a
biased estimator of the population mean when ‘N’ is not a multiple of ‘n’
can be overcome through circular systematic sampling. This system
consists of choosing a random start from 1 to N and selecting the unit
corresponding to this corresponding to this start and every kth unit in a
cyclical manner

18. That is, if r is a number sample on n units obtained k being
integer nearest to (N/n). That is, if r is a number selected at
random from 1 to N

20. APPLICATIONS
 Applicable when population is small, homogeneous & readily
available
 All subsets of the frame are given an equal probability. Each
element of the frame thus has an equal probability of selection.
 It provides for greatest number of possible samples. This is done
by assigning a number to each unit in the sampling frame.
 A table of random number or lottery system is used to determine
which units are to be selected.

21.  Disadvantage is that it is very difficult to achieve (i.e. time, effort
and money)
 The process of selection can interact with a hidden periodic trait within the
population.
 If the sampling technique coincides with the periodicity of the trait,
the sampling technique will no longer be random and representativeness
of the sample is compromised.