Документ представляет собой учебный материал по свойствам и графикам функции синус для студентов первого курса. Он включает в себя изучение основных характеристик функции синуса, ее периодичности и значений на различных интервалах, а также задачи для закрепления материала. Учебник также содержит графики и примеры, помогающие визуализировать изучаемые концепции.

1. Свойства и график функции
СИНУС
Математика. 1 курс.
По учебнику Ш.А.Алимова
Дроздова Светлана Александровна,
учитель математики ГБОУ АО СПО «Астраханский
колледж строительства и экономики»

2. 1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 ☺
cos90° sin90° sin(π/4)√2/2 cos180°
sin270° sin(π/3) cos(π/6) cos360°
ctg(π/6)
tg(π/4)
sin(3π/2) cos(2π)
cos(-π/2) cos(π/3)
cos(‒π)
0
-1
√3
1
√3/2
1
√3/2
-1
0
1
1/2
-1
1
-1
Молодец!

3. x
y
1
-1
π2
p
02
-p
-π-2π 2
-3p
2
-5p
2π 2
5p
2
3p
2
py = cos(x - )
Назовите функции,
графики которых
изображены на рисунке.
y = cosx
График функции y = sinx можно получить
сдвигом графика функции у= cosх вдоль оси
абсцисс вправо на единиц
y = = sinx
π
2

4. y
-1
1
0 xp-p 2
p
2
-p
III
II I
IY III IY I II
p
2
p
2
-p
0
p - шесть клеток
О
с
ь
С
и
н
у
с
о
в
6
-p
6
p
1
-1
0
3
p
3
-p
6
p
6
-p
3
-p
3
p
-2p
3
2p
3
-5p
6
5p
6
-2p
3
2p
3
-5p
6
5p
6
Построение графика функции y = sinx с
применением тригонометрического круга

5. p
p
2
-p
2
0
1-1 0-p
p - три клетки
x
y
1
-1
π2
p
02
-p
-π-2π 2
-3p
2
-5p
2π 2
5p
2
3p
Создание шаблона графика функции
y = sinx
Ось синусов
+
--
+
sin0 = 0
sin = 12
p
sinp = 0
sin = -12
-p
sin(-p) = 0
Полный круг

6. x
y
1
-1
π2
p
02
-p
-π-2π 2
-3p
2
-5p
2π 2
5p
2
3p
Основные свойства функции
у=sinx
Область определения
- множество R всех действительных чисел
Множество значений
- отрезок [-1; 1]Периодическая
Период 2π
, Т=2π
Нечётная, график симметричен относительно
начала координатНули функции: У=0 при х=πk, k ϵ Z

7. x
y
1
-1
π2
p
02
-p
-π-2π 2
-3p
2
-5p
2π 2
5p
2
3p
IIIIIIIIIIIIIIIIIIIIIIII
Функция возрастает
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
при х ϵ [- - +2πk ; - + 2πk ]π
2
π
2
, k ϵ Z
Функция убывает
IIIIIIIIIIIIIIIIIIIIIIII IIIIIIIIIIIIIIIIIIIIIIII
при х ϵ [ - +2πk; - +2πk]2
π 3π
2
, k ϵ Z

8. x
y
1
-1
π2
p
02
-p
-π-2π 2
-3p
2
-5p
2π 2
5p
2
3p
Функция принимает положительные
значения на интервалах (0+2πk; π+2πk),
т.е., на интервалах (2πk; π+2πk), k ϵ Z.
Функция принимает
отрицательные значения
на интервалах (π+2πk; 2π+2πk), k ϵ Z.

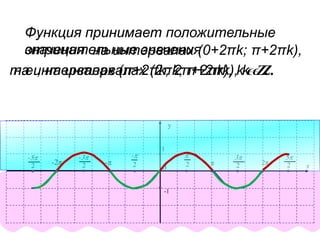
9. x
y
1
-1
π2
p
02
-p
-π-2π 2
-3p
2
-5p
2π 2
5p
2
3p
Задача 1. Найти все корни уравнения sinx= ,
принадлежащие отрезку [-π; 2π].
1
2
у=sinху= 1
2
π
6
5π
6
Ответ: х1= , х2 =6
π 5π
6
х1=arcsin =1
2
π
6 х2=π- =6
π 5π
6

10. x
y
1
-1
π2
p
02
-p
-π-2π 2
-3p
2
-5p
2π 2
5p
2
3p
Задача 2. Найти все решения неравенства
sinx< , принадлежащие отрезку [-π; 2π].1
2
у=sinху= 1
2
π
6
5π
6
IIIIIIIIIIIIIIIIIIIIIIIIIIIII IIIIIIIIIIIIIIIIIIIIIIIIIIIII
хϵ [-π; ) ( ;2π]π
6 6
5π
Ответ:

11. Каким вопросам был посвящен урок?
Чему научились на уроке?





 Выполнить задание № 729
§41. Выучить свойства функции у=sinx
Выполнить задания: № 724(2,3), № 725
Повторить преобразования графиков функции