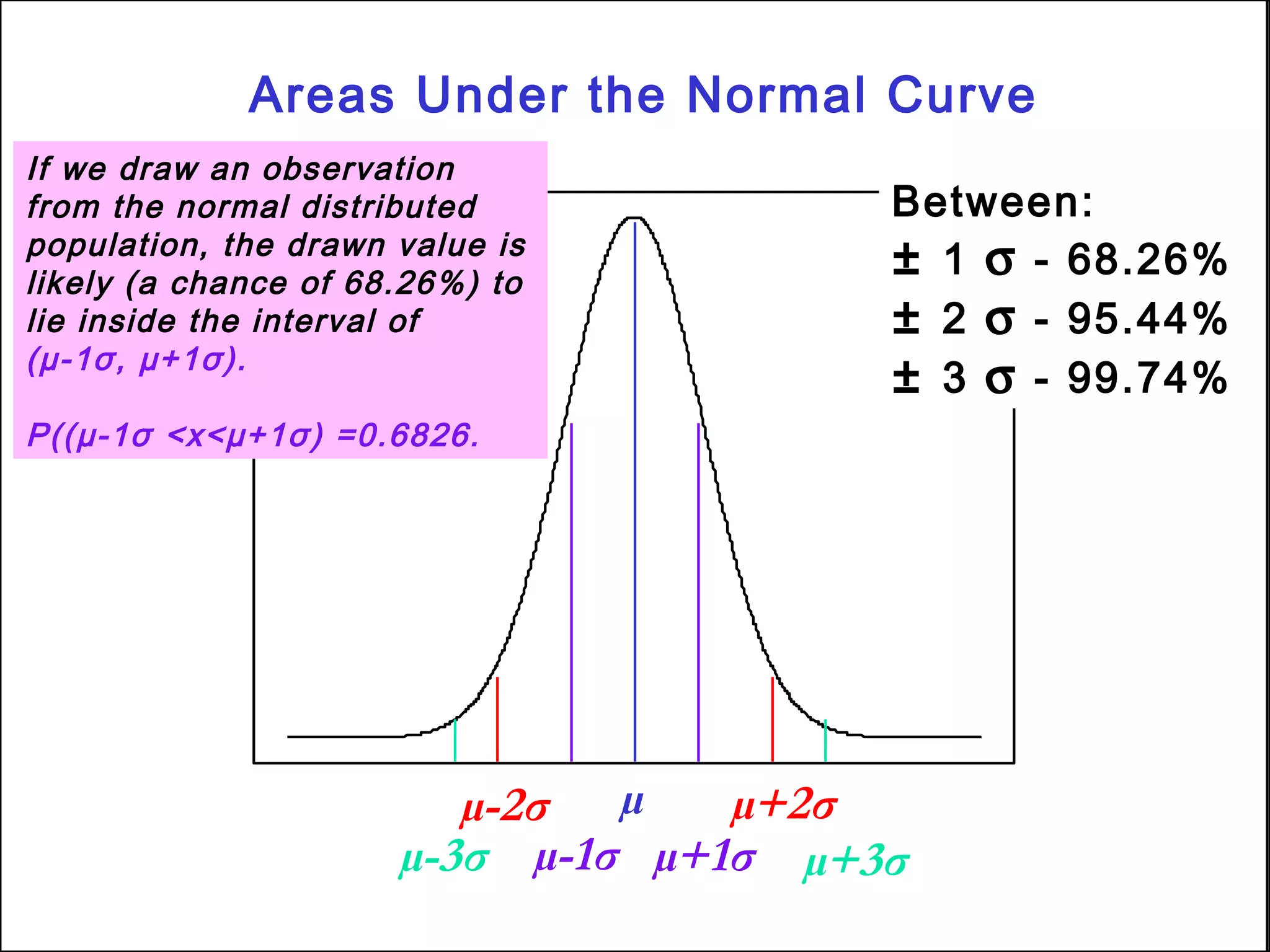
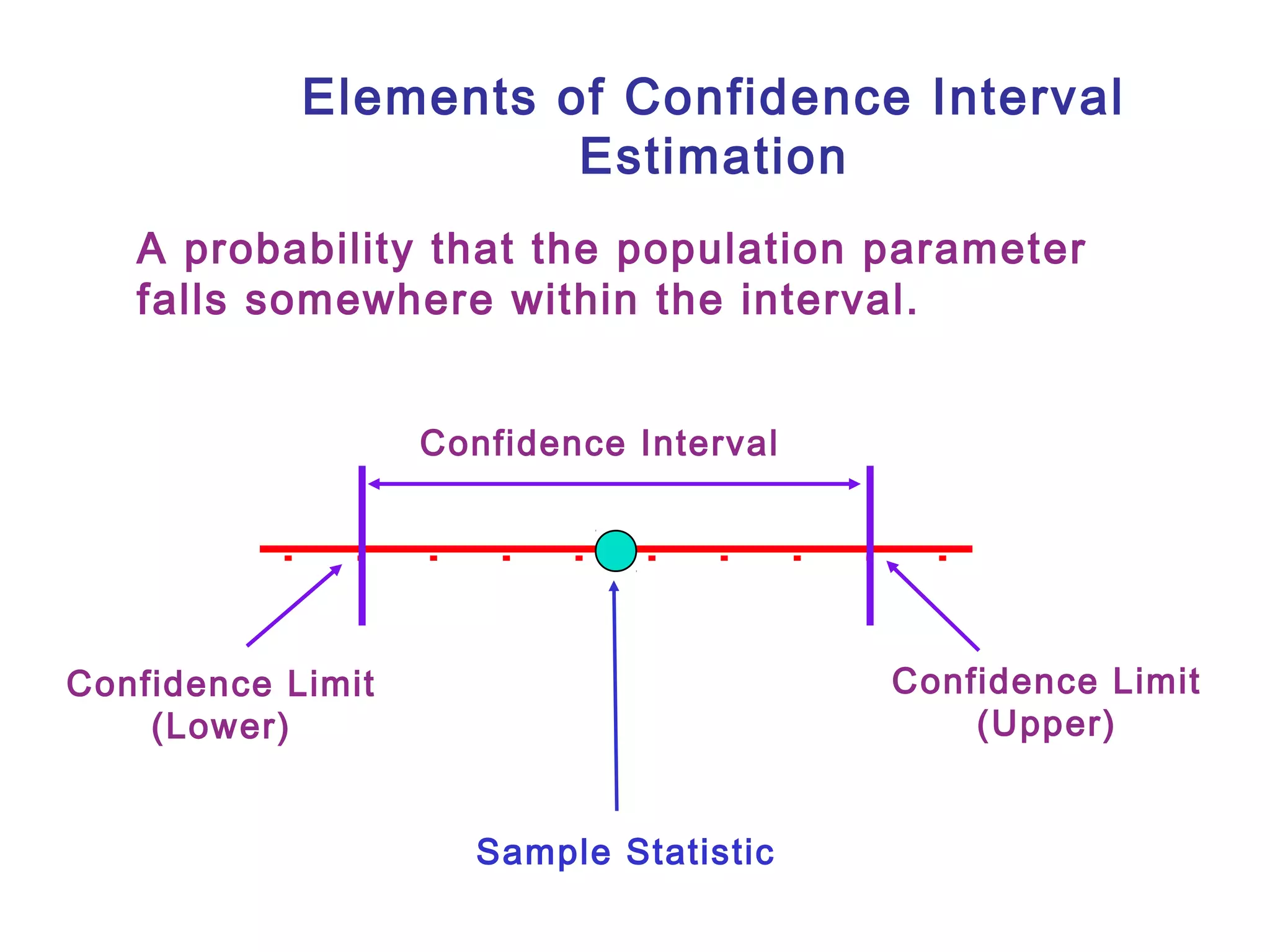
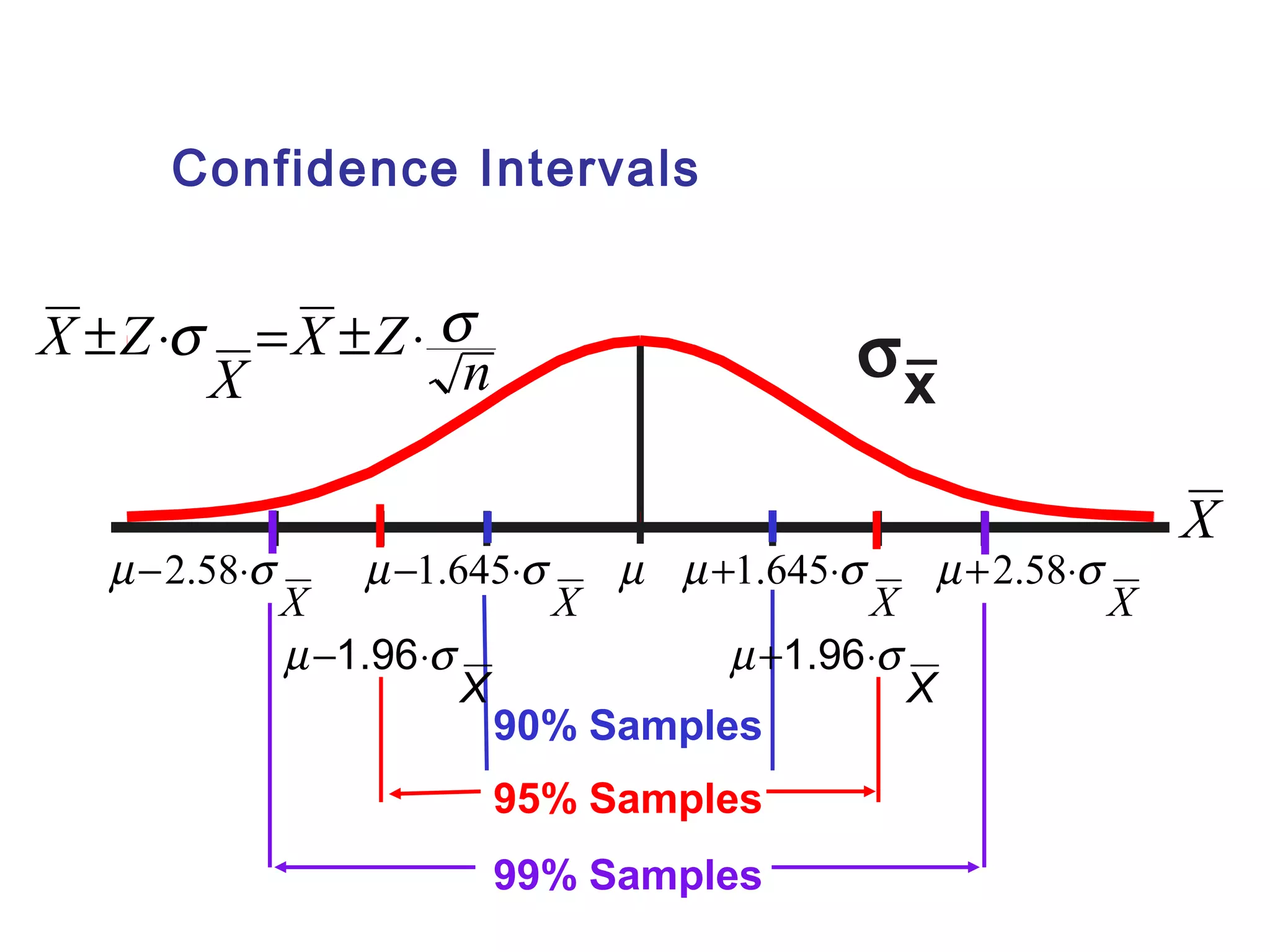
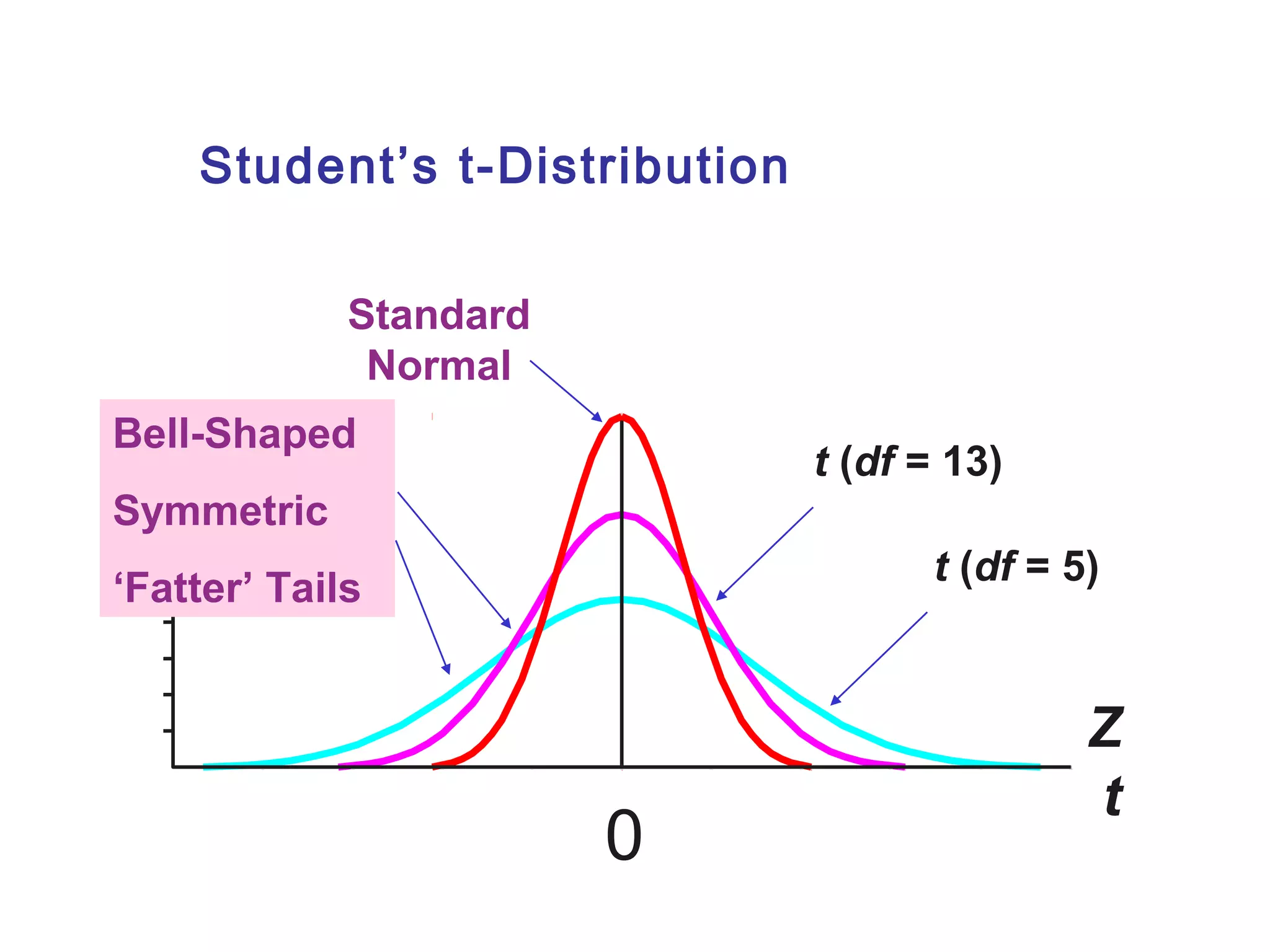
This document outlines key concepts related to estimation and confidence intervals. It defines point estimates as single values used to estimate population parameters and interval estimates as ranges of values within which the population parameter is expected to occur. Confidence intervals provide an interval range based on sample observations within which the population parameter is expected to fall at a specified confidence level, such as 95% or 99%. The document discusses how to construct confidence intervals for the population mean when the population standard deviation is known or unknown.