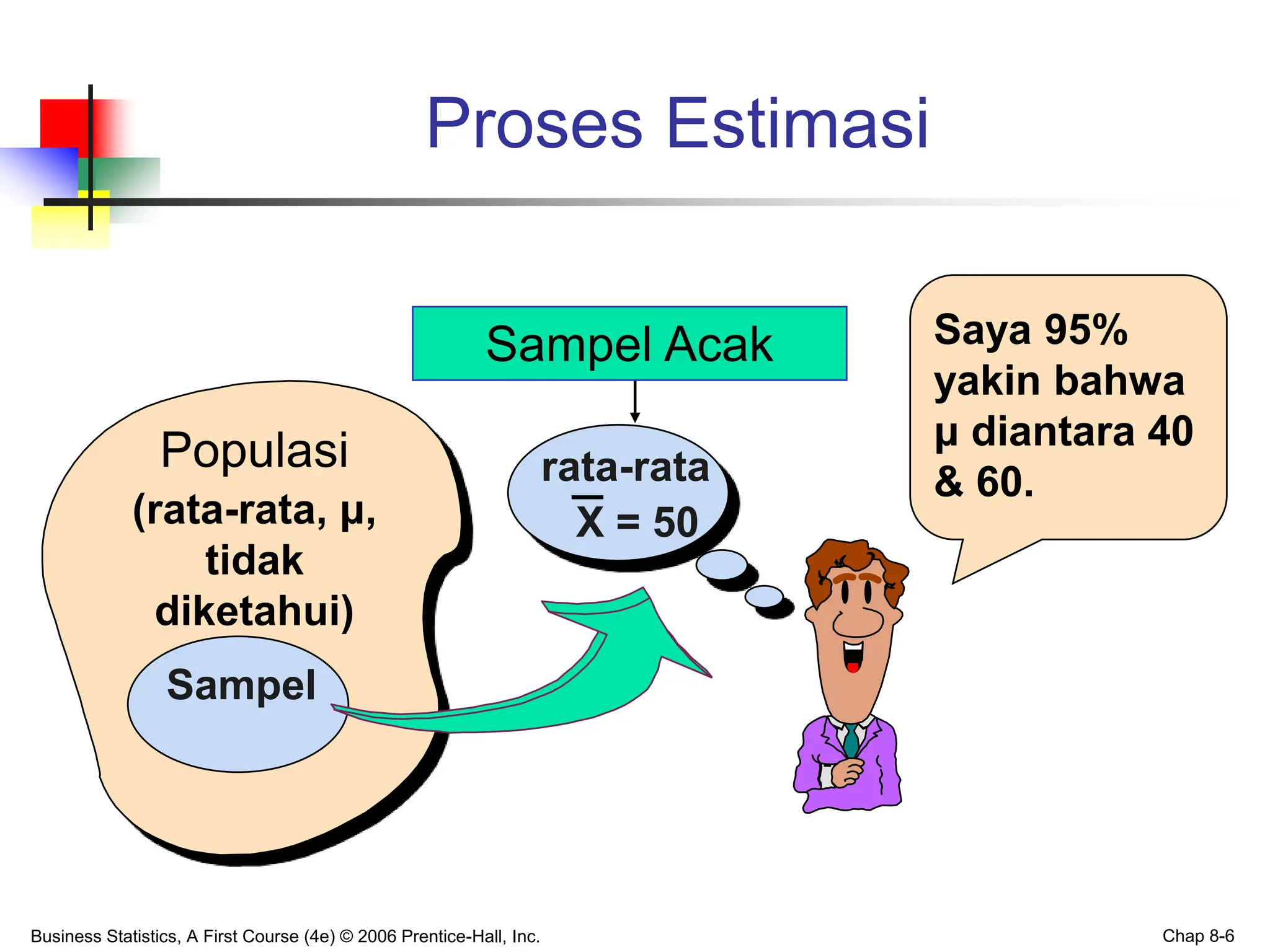
Bab ini membahas tentang estimasi interval kepercayaan dalam statistik bisnis, termasuk cara membangun dan menginterpretasikan estimasi untuk rata-rata dan proporsi populasi, serta menentukan ukuran sampel yang diperlukan. Estimasi dilakukan baik ketika simpangan baku populasi diketahui maupun tidak, dengan menggunakan distribusi normal atau distribusi t sesuai kebutuhan. Pembaca juga diberikan contoh aplikasi dari interval kepercayaan serta metode untuk menentukan ukuran sampel yang tepat.

1. Business Statistics, A First Course (4e) © 2006 Prentice-Hall, Inc. Chap 8-1
BAB 8
Estimasi Interval Kepercayaan
Statistika Bisnis

2. Business Statistics, A First Course (4e) © 2006 Prentice-Hall, Inc. Chap 8-2
Tujuan Kuliah
Pada Bab ini Anda akan belajar:
 Membangun dan menginterpretasikan
estimasi interval kepercayaan untuk rata-rata
dan proporsi
 Bagaimana menentukan ukuran sampel dari
interval kepercayaan rata-rata atau proporsi

3. Business Statistics, A First Course (4e) © 2006 Prentice-Hall, Inc. Chap 8-3
Interval Kepercayaan
Isi dalam bab ini:
 Interval Kepercayaan untuk rata-rata
populasi, μ
 Ketika simpangan baku populasi σ diketahui
 Ketika simpangan baku populasi σ tidak diketahui
 Interval Kepercayaan untuk Proporsi
Populasi, π
 Menentukan Ukuran Sampel

4. Business Statistics, A First Course (4e) © 2006 Prentice-Hall, Inc. Chap 8-4
Poin Estimasi dan Interval
 Poin estimasi berupa angka tunggal,
 Interval kepercayaan menghasilkan informasi
tambahan tentang variasi rata-rata dari
populasi
Poin Estimasi
Limit bawah
interval
kepercayaan
Limit atas
interval
kepercayaan
Lebar dari
Interval Kepercayaan

5. Business Statistics, A First Course (4e) © 2006 Prentice-Hall, Inc. Chap 8-5
Kita bisa memperkirakan
Parameter Populasi …
Poin Estimasi
Dengan Statistik
Sampel
(Poin Estimasi)
rata-rata
Proportion p
π
X
μ

6. Business Statistics, A First Course (4e) © 2006 Prentice-Hall, Inc. Chap 8-6
Proses Estimasi
(rata-rata, μ,
tidak
diketahui)
Populasi
Sampel Acak
rata-rata
X = 50
Sampel
Saya 95%
yakin bahwa
μ diantara 40
& 60.

7. Business Statistics, A First Course (4e) © 2006 Prentice-Hall, Inc. Chap 8-7
Interval Kepercayaan
Rata-rata
Populasi
σ Tidak
diketahui
Interval
Kepercayaan
Proporsi
Populasi
σ Diketahui

8. Business Statistics, A First Course (4e) © 2006 Prentice-Hall, Inc. Chap 8-8
Formula Umum
 Formula umum untuk
estimasi tingkat kepercayaan
adalah:
Poin Estimasi ± (Nilai Kritis)(Standard Error)

9. Business Statistics, A First Course (4e) © 2006 Prentice-Hall, Inc. Chap 8-9
Level Kepercayaan untuk μ
(σ diketahui)
 Asumsi
 Simpangan baku populasi σ diketahui
 Populasi terdistribusi normal
 Bila populasi tidak normal, gunakan ukuran sampel yang besar
 Estimasi Level Kepercayaan:
dimana : poin estimasi
Z : nilai kritis distribusi normal untuk probabilitas /2 dalam setiap tail (ekor)
: standard error
n
σ
Z
X 
X
n
σ/

10. Business Statistics, A First Course (4e) © 2006 Prentice-Hall, Inc. Chap 8-10
Level Kepercayaan, (1-)
 Contoh level kepercayaan = 95%
 Bisa juga ditulis (1 - ) = 0.95
  adalah level signifikansi
  = 0.05
(lanjutan)

11. Business Statistics, A First Course (4e) © 2006 Prentice-Hall, Inc. Chap 8-11
Menemukan Nilai Kritis, Z
 Level Kepercayaan 95% :
Z= -1.96 Z= 1.96
0.95
1 

0.025
2

α
0.025
2

α
Point Estimate
Lower
Confidence
Limit
Upper
Confidence
Limit
Z units:
X units: Point Estimate
0
1.96
Z 


12. Business Statistics, A First Course (4e) © 2006 Prentice-Hall, Inc. Chap 8-12
Level Kepercayaan
 Biasanya menggunakan level kepercayaan
90%, 95%, dan 99%
Level
Kepercayaan
Confidence
Coefficient, Z value
1.28
1.645
1.96
2.33
2.58
3.08
3.27
0.80
0.90
0.95
0.98
0.99
0.998
0.999
80%
90%
95%
98%
99%
99.8%
99.9%


1

13. Business Statistics, A First Course (4e) © 2006 Prentice-Hall, Inc. Chap 8-13
2.4068
1.9932
0.2068
2.20
)
11
(0.35/
1.96
2.20
n
σ
Z
X








Contoh
 11 sampel circuits dari populasi yang besar
dan normal mempunyai rata-rata hambatan
2.2 ohm. Diketahui dari penelitan bahwa
simpangan baku populasi adalah 0.35 ohm.
Level kepercayaan 95%
 Solusi:

14. Business Statistics, A First Course (4e) © 2006 Prentice-Hall, Inc. Chap 8-14
Interpretasi
 Kita yakin dengan level kepercayaan 95%
bahwa rata-rata populasi hambatan antara
1.9932 dan 2.4068 ohm.

15. Exercise
1. A sample of 49 observations is taken from a
normal population with a standard deviation of
10. The sample mean is 55. Determine the
99% confidence interval for the population
mean.
2. A sample of 81 observations is taken from a
normal population with a standard deviation of
5. The sample mean is 40. Determine the 95%
confidence interval for the population mean.
Business Statistics, A First Course (4e) © 2006 Prentice-Hall, Inc. Chap 8-15

16. Business Statistics, A First Course (4e) © 2006 Prentice-Hall, Inc. Chap 8-16
Interval Kepercayaan
Rata-rata
Populasi
σ
tidak
diketahui
Interval
Kepercayaan
Proporsi
Populasi
σ
diketahui

17. Business Statistics, A First Course (4e) © 2006 Prentice-Hall, Inc. Chap 8-17
 Bila simpangan baku populasi σ tidak
diketahui, kita bisa subsitusi memakai
simpangan baku sampel, S
 Kemudian kita memakai distribusi t,
bukan distribusi normal
Interval Kepercayaan untuk μ
(σ tidak diketahui)

18. Chap 8-18
 Asumsi
 Simpangan baku Populasi tidak diketahui
 Populasi terdistribusi normal
 Bila populasi tidak terdistribusi normal, ambil ukuran sampel
yang besar
 Memakai Distribusi t (Student’s t Distribution)
 Estimasi Interval Kepercayaan:
(dimana t adalah nilai kritis dari distribusi t dengan n -1 adalah
derajat kebebasan dan area α/2 dalam setiap tail)
Interval Kepercayaan untuk μ
(σ tidak diketahui)
n
S
t
X 1
-
n

(lanjutan)

19. Business Statistics, A First Course (4e) © 2006 Prentice-Hall, Inc. Chap 8-19
Distribusi t
 Nilai t tergantung dari derajat kebebasan /
degrees of freedom (d.f.)
 Jumlah pengamatan yang bebas bervariasi setelah rata-rata
sampel dihitung
d.f. = n - 1

20. Business Statistics, A First Course (4e) © 2006 Prentice-Hall, Inc. Chap 8-20
If the rata-rata of these
three values is 8.0,
then X3 must be 9
(i.e., X3 is not free to vary)
Degrees of Freedom (df)
disini, n = 3, sehingga derajat kebebasan = n – 1 = 3 – 1 = 2
(2 angka bisa berapa saja, tapi angka yang ketiga tidak bisa
dipilih bebas)
Ide: Jumlah pengamatan yang bebas bervariasi
setelah rata-rata sampel dihitung
Contoh: rata-rata dari 3 angka adalah 8.0
X1 = 7
X2 = 8
Berapa X3?

21. Business Statistics, A First Course (4e) © 2006 Prentice-Hall, Inc. Chap 8-21
Distribusi t
t
0
t (df = 5)
t (df = 13)
Distribusi-t berbentuk lonceng
dan simetrik, tapi mempunyai
ekor yang lebih gendut drpd
distribusi normal
Standard
Normal
(t with df = ∞)
Catatan: t Z bila n meningkat

22. Business Statistics, A First Course (4e) © 2006 Prentice-Hall, Inc. Chap 8-22
Tabel t
Upper Tail Area
df .25 .10 .05
1 1.000 3.078 6.314
2 0.817 1.886 2.920
3 0.765 1.638 2.353
t
0 2.920
Harga dari nilai-t, tapi
bukan merupakan
probabilitas
Let: n = 3
df = n - 1 = 2
 = 0.10
/2 = 0.05
/2 = 0.05

23. Business Statistics, A First Course (4e) © 2006 Prentice-Hall, Inc. Chap 8-23
Nilai distribusi-t
Perbandingan dengan nilai-Z
Confidence t t t Z
Level (10 d.f.) (20 d.f.) (30 d.f.) ____
0.80 1.372 1.325 1.310 1.28
0.90 1.812 1.725 1.697 1.645
0.95 2.228 2.086 2.042 1.96
0.99 3.169 2.845 2.750 2.58
Catatan: t Z ketika n meningkat

24. Business Statistics, A First Course (4e) © 2006 Prentice-Hall, Inc. Chap 8-24
Contoh
Sampel acak dari n = 25 diambil dari populasi
normal, mempunyai X = 50 dan S = 8. Bentuk
Level kepercayaan 95% untuk μ
 d.f. = n – 1 = 24, jadi
Interval kepercayaannya adalah
2.0639
t0.025,24
1
n
,
/2 



t
𝑋 ± 𝑡𝛼/2, n−1
S
n
= 50 ± (2.0639)
8
25
46.698 ≤ μ ≤ 53.302

25. Business Statistics, A First Course (4e) © 2006 Prentice-Hall, Inc. Chap 8-25
Interpretasi
 Kita yakin dengan level kepercayaan 95%
bahwa rata-rata populasi antara 46.698
dan 53.302.

26. Latihan
 Diberikan data mengenai frekuensi enam ibu
rumah tangga berbelanja di super market
dalam sebulan: 2 3 4 4 5 6.
 Buat interval kepercayaan dengan level
kepercaayaan 95% untuk rata-rata populasi.
Business Statistics, A First Course (4e) © 2006 Prentice-Hall, Inc. Chap 8-26
𝑋 ± 𝑡
S
n
= 4 ± (2.571)
1,41
6
= 4 ± 1,48
Kita yakin dengan level kepercayaan 95% bahwa rata-rata
populasi antara 2.52 dan 5.48.

27. Business Statistics, A First Course (4e) © 2006 Prentice-Hall, Inc. Chap 8-27
Interval Kepercayaan
Rata-rata
Populasi
σ
tidak
diketahui
Interval
Kepercayaan
Proporsi
Populasi
σ
diketahui

28. Business Statistics, A First Course (4e) © 2006 Prentice-Hall, Inc. Chap 8-28
Interval Kepercayaan untuk
Proporsi Populasi, π
 Estimasi interval untuk proporsi
populasi ( π ) bisa dihitung dari
proporsi sampel ( p )

29. Business Statistics, A First Course (4e) © 2006 Prentice-Hall, Inc. Chap 8-29
Interval Kepercayaan untuk
Proporsi Populasi, π
 Distribusi proprosi sampel mendekati normal
bila ukuran sampel besar, dengan simpangan
baku
 Kita akan memperkirakan nilai di atas menggunakan
data sampel:
(lanjutan)
n
p)
p(1
n
)
(1
σp

 


30. Business Statistics, A First Course (4e) © 2006 Prentice-Hall, Inc. Chap 8-30
Interval Kepercayaan
 Batas atas dan bawah interval kepercayaan bisa
dihitung menggunakan rumus:
 diman
 Z : nilai Z untuk level kepercayaan yang diinginkan
 p : proporsi sampel
 n : ukuran sampel
n
p)
p(1
Z
p



31. Business Statistics, A First Course (4e) © 2006 Prentice-Hall, Inc. Chap 8-31
Contoh
 Sampel acak dari 100 orang
memperlihatkan bahwa 25 adalah
kidal.
 Bentuk level kepercayaan 95% untuk
proporsi populasi yang kidal

32. Business Statistics, A First Course (4e) © 2006 Prentice-Hall, Inc. Chap 8-32
Contoh
 Sampel acak dari 100 orang memperlihatkan
bahwa 25 adalah kidal. Bentuk level kepercayaan
95% untuk proporsi populasi yang kidal
/100
0.25(0.75)
1.96
25/100
p)/n
p(1
Z
p




0.3349
0.1651
(0.0433)
1.96
0.25





(lanjutan)

33. Business Statistics, A First Course (4e) © 2006 Prentice-Hall, Inc. Chap 8-33
Interpretasi
 Kita yakin 95% bahwa proporsi populasi
yang kidal adalah diantara
16.51% dan 33.49%.

34. Business Statistics, A First Course (4e) © 2006 Prentice-Hall, Inc. Chap 8-34
Menentukan Ukuran Sampel
Untuk
rata-rata
Menentukan
Ukuran sampel
Untuk
Proportion

35. Business Statistics, A First Course (4e) © 2006 Prentice-Hall, Inc. Chap 8-35
Menentukan Ukuran Sampel
Untuk
rata-rata
Menentukan
Ukuran sampel
n
σ
Z
X 
n
σ
Z
e 
Sampling error
(margin of error)

36. Business Statistics, A First Course (4e) © 2006 Prentice-Hall, Inc. Chap 8-36
Menentukan Ukuran Sampel
Untuk
rata-rata
Menentukan
Ukuran sampel
n
σ
Z
e 
(lanjutan)
2
2
2
e
σ
Z
n 
Rumus
untuk
mencari n

37. Business Statistics, A First Course (4e) © 2006 Prentice-Hall, Inc. Chap 8-37
Menentukan Ukuran Sampel
 Untuk menentukan ukuran sampel yang
diinginkan untuk rata-rata, kita harus
mengetahui:
 Level kepercayaan yang diinginkan (1 - ), dimana
akan menentukan nilai kritis Z
 sampling error yang dapat diterima, e
 Simpangan baku, σ
(lanjutan)

38. Business Statistics, A First Course (4e) © 2006 Prentice-Hall, Inc. Chap 8-38
Contoh
Jika  = 45, Berapakah ukuran sampel yang
diperlukan bila sampling error yang bisa
diterima ± 5 dengan level kepercayaan 90%?
(Selalu dibulatkan ke
atas)
219.19
5
(45)
(1.645)
e
σ
Z
n 2
2
2
2
2
2



Jadi Ukuran sampel yang diperlukan adalah n = 220

39. Business Statistics, A First Course (4e) © 2006 Prentice-Hall, Inc. Chap 8-39
Jika σ tidak diketahui
 Bila tidak diketahui, σ bisa diperkirakan
dengan memakai rumus sebelumnya
 Gunakan simpangan baku sampel S,
untuk memperkirakan σ

40. Business Statistics, A First Course (4e) © 2006 Prentice-Hall, Inc. Chap 8-40
Menentukan Ukuran Sampel
Menentukan
Ukuran Sampel
Untuk
Proporsi
2
2
e
)
(1
Z
n
π
π 

Diperoleh
rumus
untuk
mencari n
n
)
(1
Z
e
π
π 

(lanjutan)

41. Business Statistics, A First Course (4e) © 2006 Prentice-Hall, Inc. Chap 8-41
Contoh
Berapa besar ukuran sampel yang
diperlukan bila sampling error yang bisa
diterima adalah ±3%, dengan level
kepercayaan 95%?
(Asumsikan p = 0.12)

42. Business Statistics, A First Course (4e) © 2006 Prentice-Hall, Inc. Chap 8-42
Contoh
Solusi:
Untuk level kepercayaan 95%, Z = 1.96
e = 0.03
p = 0.12, maka gunakan nilai p untuk
memperkirakan nilai π
Dibulatkan n = 451
450.74
(0.03)
0.12)
(0.12)(1
(1.96)
e
)
(1
Z
n 2
2
2
2





π
π
(lanjutan)

43. Home Work
Business Statistics, A First Course (4e) © 2006 Prentice-Hall, Inc. Chap 8-43
1. Suatu lembaga penelitian mengadakan survey sederhana untuk
mengetahui besarnya rata-rata pengeluaran para wisatawan asing
yang berkunjung ke pulau dewata Bali. Untuk itu dilakukan
pengambilan sampel responden secara acak (simple random
sampling) sebanyak 100 wisatawan asing yang menginap di
beberapa hotel. Dari survey diperoleh bahwa rata-rata pengeluaran
per kunjungan adalah $ 800 per wisatawan. Jika diketahui deviasi
standar populasi dari pengeluaran semua wisatawan yang
berkunjung ke Bali adalah $ 120, maka buatlah interval estimasi
dengan level keyakinan (confidence level) 95 % untuk menduga rata-
rata pengeluaran per wisatawan asing yang berkunjung ke Bali.