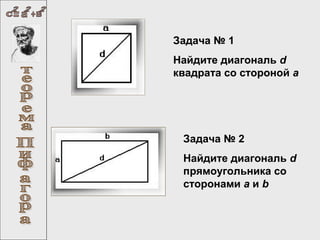
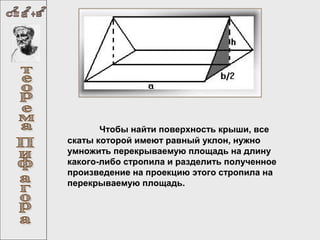
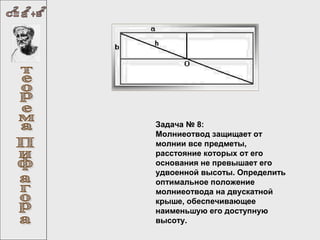
Документ содержит множество математических задач, включая нахождение диагоналей фигур, исследование пирамиды, расчет скоростей самолетов, построение готических окон и оптимизацию высоты молниеотвода. Также упоминается великая теорема Ферма и ее исторический контекст. Каждая задача требует применения различных математических принципов и теорий.

1. Выполнила Сергеева Виктория

2. Задача № 1
Найдите диагональ d
квадрата со стороной a
Задача № 2
Найдите диагональ d
прямоугольника со
сторонами a и b

3. Задача № 3
Найти диагональ куба d,
если ребро куба a
Задача № 4
Исследуем пирамиду,
например, такую в основании
которой лежит квадрат, и
высота которой проходит
через центр квадрата. Пусть
сторона квадрата a, а высота
пирамиды h. Чему равна длина
S боковых рёбер пирамиды?

4. Чтобы найти поверхность крыши, все
скаты которой имеют равный уклон, нужно
умножить перекрываемую площадь на длину
какого-либо стропила и разделить полученное
произведение на проекцию этого стропила на
перекрываемую площадь.

5. Задача № 5:
С аэродрома вылетели одновременно
два самолёта: один - на запад, другой - на
юг. Через два часа расстояние между ними
было 2000 км. Найдите скорости самолётов,
если скорость одного составляла 75%
скорости другого.

6. Задача № 6:
Как следовало бы поступить
юному математику, чтобы надёжным
образом получить прямой угол?
Задача № 7:
Найдите равнодействующую трёх
сил по 200 Н каждая, если угол между
первой и второй силами и между
второй и третьей силами равен 60°.

7. В зданиях романского и готического
стиля верхние части окон
расчленяются каменными рёбрами,
которые не только играют роль
орнамента, но и способствуют
прочности окон. На рисунке
представлен простой пример такого
окна в готическом стиле. Способ
построения его весьма прост: из
рисунка легко найти центры шести дуг
окружностей, радиусы которых равны
1)ширине окна b для наружных дуг и 2)
половине ширины, т.е. b/2 -для
внутренних. Остаётся ещё полная
окружность, касающаяся четырёх дуг.
Так как она заключена между двумя
концентрическими окружностями, то её
диаметр равен расстоянию между
этими окружностями, т.е. b/2 и,
следовательно, радиус равен b/4.
Тогда становится ясным и положение
её центров.

8. В романской архитектуре часто
встречается мотив,
представленный на этом
рисунке.
Если b по-прежнему обозначает
ширину окна, то радиусы
полуокружностей будут равны
R=b/2 и r =b/4. Радиус ρ
внутренней окружности можно
вычислить из прямоугольного
треугольника, изображённого на
рисунке пунктиром. Гипотенуза
этого треугольника, проходящая
через точку касания
окружностей, равна b/4+ρ, один
катет равен b/4, а другой b/2-ρ.
По теореме Пифагора имеем:
(b/4+ρ)2=(b/4)2+(b/2-ρ)2
или
b2/16+bρ /2+ρ2=b2/16+b2/4bρ+ρ2,

9. Задача № 8:
Молниеотвод защищает от
молнии все предметы,
расстояние которых от его
основания не превышает его
удвоенной высоты. Определить
оптимальное положение
молниеотвода на двускатной
крыше, обеспечивающее
наименьшую его доступную
высоту.

10. Задача №9:
Какую наибольшую высоту
должна иметь
телевизионная вышка,
чтобы передачу можно
было принимать в радиусе
R=200 км? (радиус Земли
равен 6380 км.)

11. Пифагорово уравнение
х2 + у2 = z2
является частным случаем уравнения
хn + уn = zn ,
по поводу которого знаменитый математик
Пьер Ферма около 1635 года небрежно
заметил, что оно не имеет решений в
натуральных числах x, y, z, n, если n > 1. Это
утверждение вошло в математику под
названием Великой теоремы Ферма.