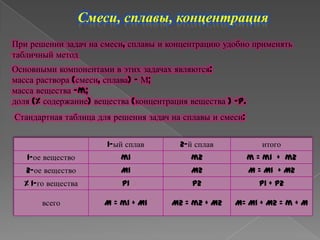
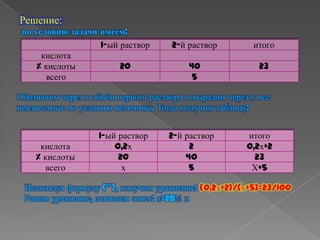
Документ содержит учебные задачи и решения по теме процентов, сплавов и смесей, описывая, как вычислять проценты, находить части от целого и решать задачи на смешивание веществ. Приведены примеры, такие как расчет масла в сое, волокна из хлопка-сырца и содержание соли в морской воде. Методика решения включает применение дробей и уравнений для нахождения неизвестных величин и процентного соотношения.

1. Подготовили ученицы 8 «Б» класса:
Кисель Юлия
Плешкова Екатерина
Франц Анна

2. Проценты
Определение: процентом называется дробь 1/100 (0,01).
Чтобы выразить число в процентах, надо это число умножить на 100,
Например:
(0,58  100)% = 58 %
Чтобы выразить процент десятичной дробью или натуральным
числом, нужно число, стоящее перед знаком %, разделить на 100.
Например:
37 % = 37/100 = 0,37

3. Чтобы найти несколько процентов от числа, надо проценты выразить
дробью, а затем найти дробь от данного числа.
Задача. В семенах сои содержится 20 % масла. Сколько масла содержится в
700 кг сои?
Решение.
В задаче требуется найти указанную часть (20 %) от известной величины
(700 кг). Такие задачи можно решать способом приведения к единице.
Основное значение величины – 700 кг. Еѐ мы можем принять за условную
единицу. А условная единица и есть 100 %.
Кратко условия задачи можно записать так:
700 кг – 100 %
Х кг – 20 %.
Здесь за Х принята искомая масса масла. Узнаем, какая масса сои приходится
на 1 %. Поскольку на 100 % приходится 700 кг, то на 1 % будет приходиться
масса, в сто раз меньшая, то есть 700 : 100 = 7 (кг). Значит, на 20 % будет
приходиться в 20 раз больше: 7 х 20 = 140 (кг). Следовательно, в 700 кг сои
содержится 140 кг масла.

4. Чтобы найти число по данным его процентам, надо выразить проценты
в виде дроби и решить задачу на нахождение числа по данной его дроби.
Задача.
Из хлопка-сырца получается 24 % волокна. Сколько надо взять хлопка-
сырца, чтобы получить 480 кг волокна?
Решение
480 кг волокна составляют 24 % от некоторой массы хлопка-сырца, которую
примем за Х кг. Будем считать, что Х кг составляют 100 %. Теперь кратко
условие задачи можно записать так:
480 кг - 24 %
Х кг - 100 %
Решим эту задачу способом приведения к единице. Узнаем, какая масса
волокна приходится на 1 %. Поскольку на 24 % приходится 480
кг, то, очевидно, на 1 % будет приходиться масса в 24 раза меньше, то есть
480 : 24 = = 20 (кг). Далее рассуждаем так: если на 1 % приходится масса в
20 кг, то на 100 % будет приходиться масса, в 100 раз большая, то есть 20 х
100 = 2000 (кг)
= 2 (т). Следовательно, для получения 480 кг волокна надо взять 2 т хлопка-
сырца.

5. Чтобы найти процентное отношение двух чисел, надо найти
отношение этих чисел и выразить его в процентах.
Задача
Надо вспахать участок поля в 500 га. В первый день вспахали 150 га. Сколько
процентов составляет вспаханный участок от всего участка?
Решение
Чтобы ответить на вопрос задачи, надо найти отношение (частное)
вспаханной части участка ко всей площади участка и выразить его отношение
в процентах:
150/500 = 3/10 = 0,3 = 30 %
Таким образом, мы нашли процентное отношение, то есть сколько процентов
одно число (150) составляет от другого числа (500).

6. Смеси, сплавы, концентрация
При решении задач на смеси, сплавы и концентрацию удобно применять
табличный метод
Основными компонентами в этих задачах являются:
масса раствора (смеси, сплава) - М;
масса вещества –m;
доля (% содержание) вещества (концентрация вещества ) -P.
Стандартная таблица для решения задач на сплавы и смеси:
1-ый сплав 2-й сплав итого
1-ое вещество m1 m2 m = m1 + m2
2-ое вещество M1 M2 M = M1 + M2
% 1-го вещества P1 P2 P1 + P2
всего M = m1 + M1 M2 = m2 + M2 M= M1 + M2 = m + M

7. Основная формула, применяемая при решении задач на сплавы:
P = m / M *100% (**)
В задачах на концентрацию, смеси, сплавы уравнение, как
правило, составляется по последнему столбцу.
Рассмотрим 2 типа наиболее часто встречающихся видов задач со смесями
и сплавами.
1тип.
Чаще всего встречаются задачи, в которых известны процентные
содержания одного и того же вещества как в двух исходных сплавах, так и
в сплаве, полученном после их соединения.
Задача:
Сколько литров 20% -го раствора кислоты надо добавить к 5 л 40%-го
раствора кислоты, чтобы получить раствор с 23% содержанием кислоты?

8. Решение:
по условию задачи имеем:
1-ый раствор 2-й раствор итого
кислота
% кислоты 20 40 23
всего 5
Обозначим через х объѐм первого раствора и выразим через х все
неизвестные по условию величины. Тогда получим таблицу:
1-ый раствор 2-й раствор итого
кислота 0,2х 2 0,2х+2
% кислоты 20 40 23
всего х 5 Х+5
Используя формулу (**), получим уравнение: (0,2х+2)/(х+5)=23/100
Решив уравнение, запишем ответ: х=28⅓ л

9. 2тип.
Одна из смесей содержит лишь один элемент. В таком случае процент
(концентрация) вещества может быть равен 0 или 100, что не всегда
понятно учащимся.
Задача:
Морская вода содержит 5% по весу соли. Сколько килограммов пресной
воды нужно прибавить к 80 кг морской, чтобы содержание соли в
последней составило 2%?
Решение:
первоначальная таблица имеет вид:
Морская вода Пресная вода итого
Вода
Соль 0
%соли 5 0 2
итого 80

10. За х примем количество добавляемой пресной воды, тогда таблица примет
вид:
Морская вода Пресная вода итого
Вода 76 х 76+х
Соль 4 0 4
%соли 5 0 2
итого 80 х 80+х
Используя формулу (**) и последний столбец таблицы получим
уравнение:
4 / (80+х) =2/100
Решив уравнение, запишем ответ: 120 кг

11. Спасибо за внимание